Binary Tree Implementation in Java

Introduction

A binary tree is a non-linear hierarchical data structure consisting of a collection of nodes that stores data forming a hierarchy. It does not store data sequentially as data structures like Arrays, Linked lists, Queues, and Stacks do. Instead, it stores data at multiple levels where each level can store at most 2 children nodes.

A tree is made of nodes, and each node contains data, a left pointer, and a right pointer. The uppermost node is referred to as the root, and the bottom-most nodes are referred to as leaf nodes. The nodes that are directly below any node are called children, and those directly above are called the parent. In the following figure, node H is the child of D, and D is the parent of H.

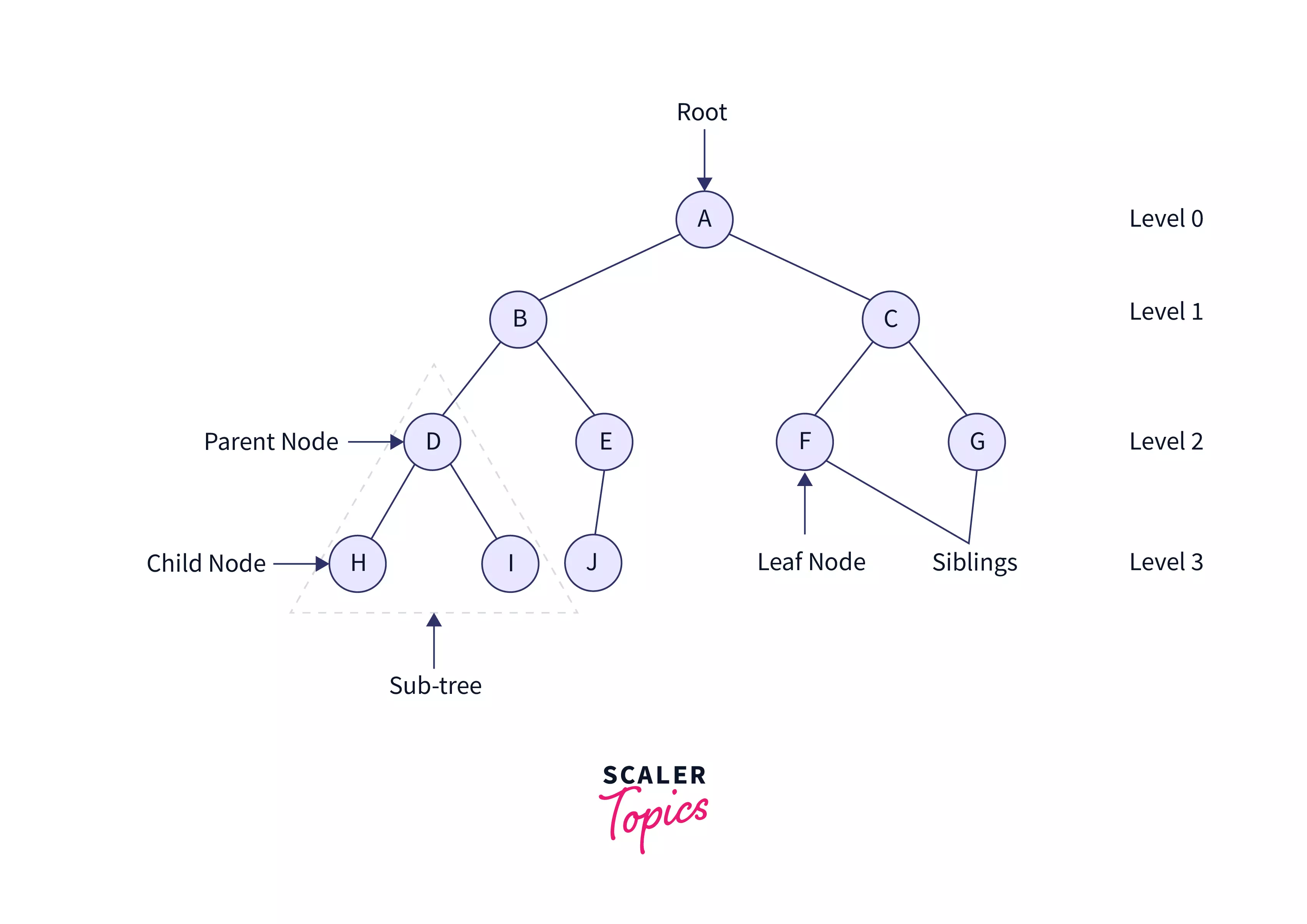
The properties of binary trees include:

• Maximum nodes on each level double as we move down the tree. This is because the Number of nodes at any level is equal to 2 raised to the power of n where n is the number of levels starting from 0.
• The maximum number of nodes in the last level is equal to one more than the sum of all the nodes in the previous level of a complete binary tree.

Let's see how it works.

Number of nodes at 0th level = 1

Number of nodes at 1st level = 2 = Number of nodes at 0th level + 1

Number of nodes at 2nd level = 4 = 1 + 2 + 1 = Number of nodes at 0th level + Number of nodes at 1st level + 1

Number of nodes at 3rd level = 8 = 1 + 2 + 4 + 1 = Number of nodes at 0th level + Number of nodes at 1st level + Number of nodes at 2nd level + 1

Therefore, the Number of nodes at nth level = Sum of nodes at all n-1 levels + 1

Binary trees have many applications in the real world. Most of the applications use variations of binary trees that are Tries, Binary Search Tree, and B-Trees. They are used for sorting, searching, grouping, and storing data hierarchically. Operations like Insertion, Deletion, and Traversal are applied to them.

Let's learn how to implement binary tree data structure in Java.

Example: Java Program to Implement Binary Tree

In Java, a tree node is implemented using a class. The data inside every node can be a string, char, integer, double, or float data type.

A binary tree can be implemented in two ways: A node representation and an array representation. The node representation is dynamic and the number of nodes can be increased as per requirement. The array representation is sequential and static. The size of the array needs to be defined at the time of creation which leads to space issues.

Let's see an example of the binary tree implementation in Java of data type int.

The above example is an implementation of a Binary Tree in Java. Since Java doesn't provide an inbuilt function for Trees, we have created a class named Binary Tree. We have created a method named traverseTree which traverses the binary tree in an inorder manner and prints the key value of all nodes.

In the main function, we have created an object of BinaryTree class named tree. We then create the nodes of the tree by putting the values in them one by one and placing them at the required positions. Calling the function traverseTree with the root as the parameter traverses the tree in an inorder manner starting from the root. The inorder uses the left root right policy. It first traverses the left subtree of the root, then the root and the right subtree of the root. For every subtree, it follows the same method of traversal.

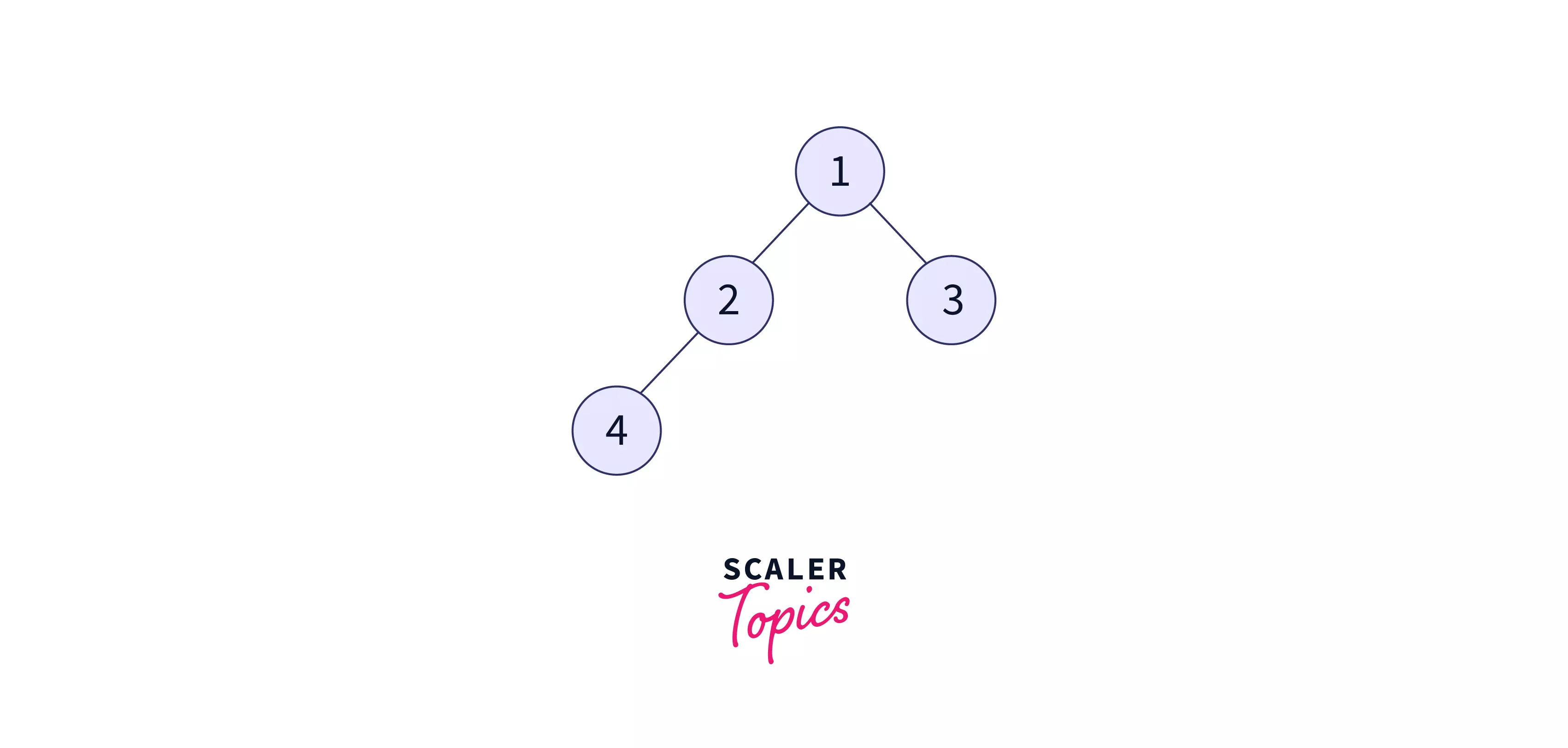
For the tree formed above, it first moves to node 1, then to its left until it encounters a null node. The last root node it encounters is 4. It prints 4 and then moves to its right which is null. It again backtracks itself to 2 as the root node and prints 2. It moves to the right subtree of 2 and encounters null. It again goes back to 1 as the root node and prints 1. It traverses the right subtree of 1 and gets 3 as the root node. Since 3 does not have any left child, 3 is printed and then the right subtree of 3 is traversed. After it is found null, the traversal is stopped as it is the extreme right node.

The above code gives us the following output:

Output:

Unlike the above example, where we manually decided the respective positions of the keys, we can also do it using the code. This is a modification of the binary tree known as the binary search tree.

A binary search tree is a variation of a binary tree data structure with the following properties:

• The left subtree contains key values lesser than the node key.
• The right subtree contains key values greater than the node key.
• Each subtree is a binary search tree.

It seems quite simple. Let's implement this logic using an example to see how it works:

Example:

Output:

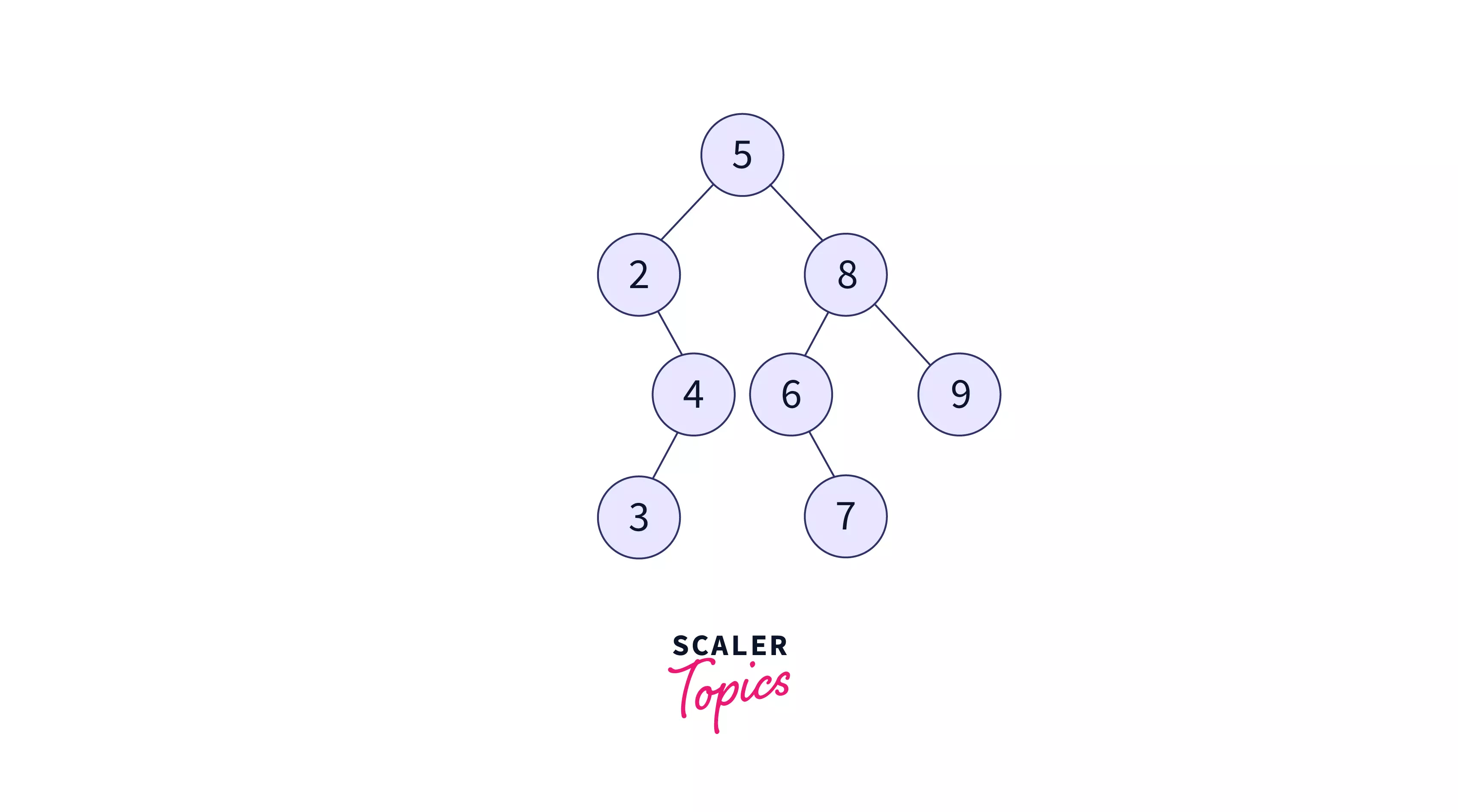
In the above example, we have created an auxiliary Node class that stores the int value as the key and the reference or address of the left and the right child. The next step involves placing the nodes in the right position to keep the binary tree sorted. It is possible if we follow the following set of rules to insert a node starting at the root node:

• if the value of the new node is less than the current node's value, traverse the left child.
• if the value of the new node is more than the current node's value, traverse the right child.
• if the value of the current node is null then insert the new node at that position as we have reached a leaf node.

The inorder traversal of the tree uses the left root right policy. It first traverses the left subtree, then moves to the root, and finally to the right subtree. The inorder traversal of a binary search tree gives a sorted and non-decreasing ordered sequence of the key values.

Binary Tree Implementation in Java Using Arrays

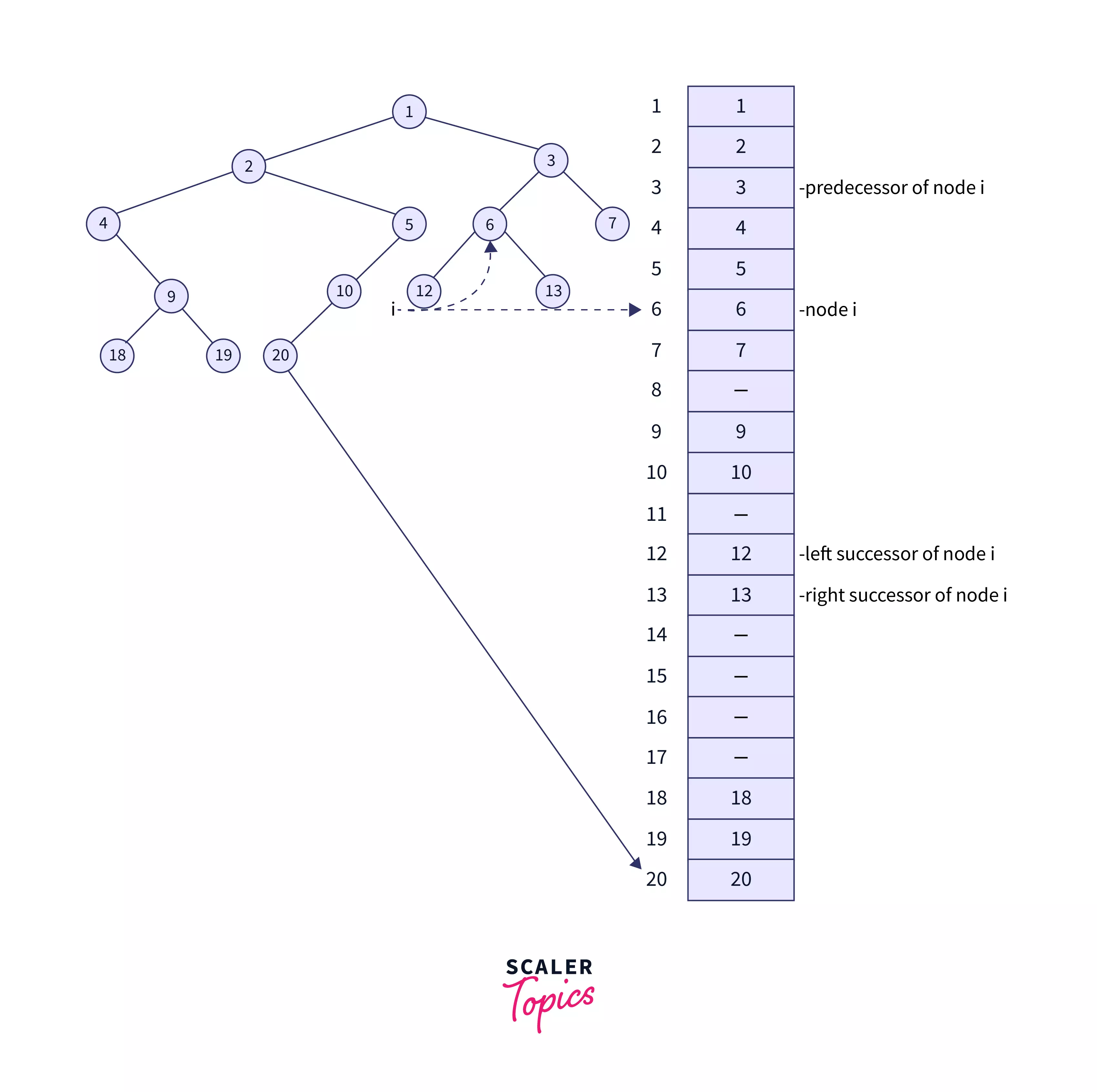
A binary tree can also be represented sequentially in the form of arrays. The sequential representation uses arrays to store information corresponding to each node. The record of the node i of the tree is stored as the ith record in the array. The numbering is done according to the preorder traversal of the tree and each node is assigned the number on its way. For representing trees in the form of arrays, the indexes of the nodes in the array can be numbered in two ways - 0 to n-1 or 1 to n.

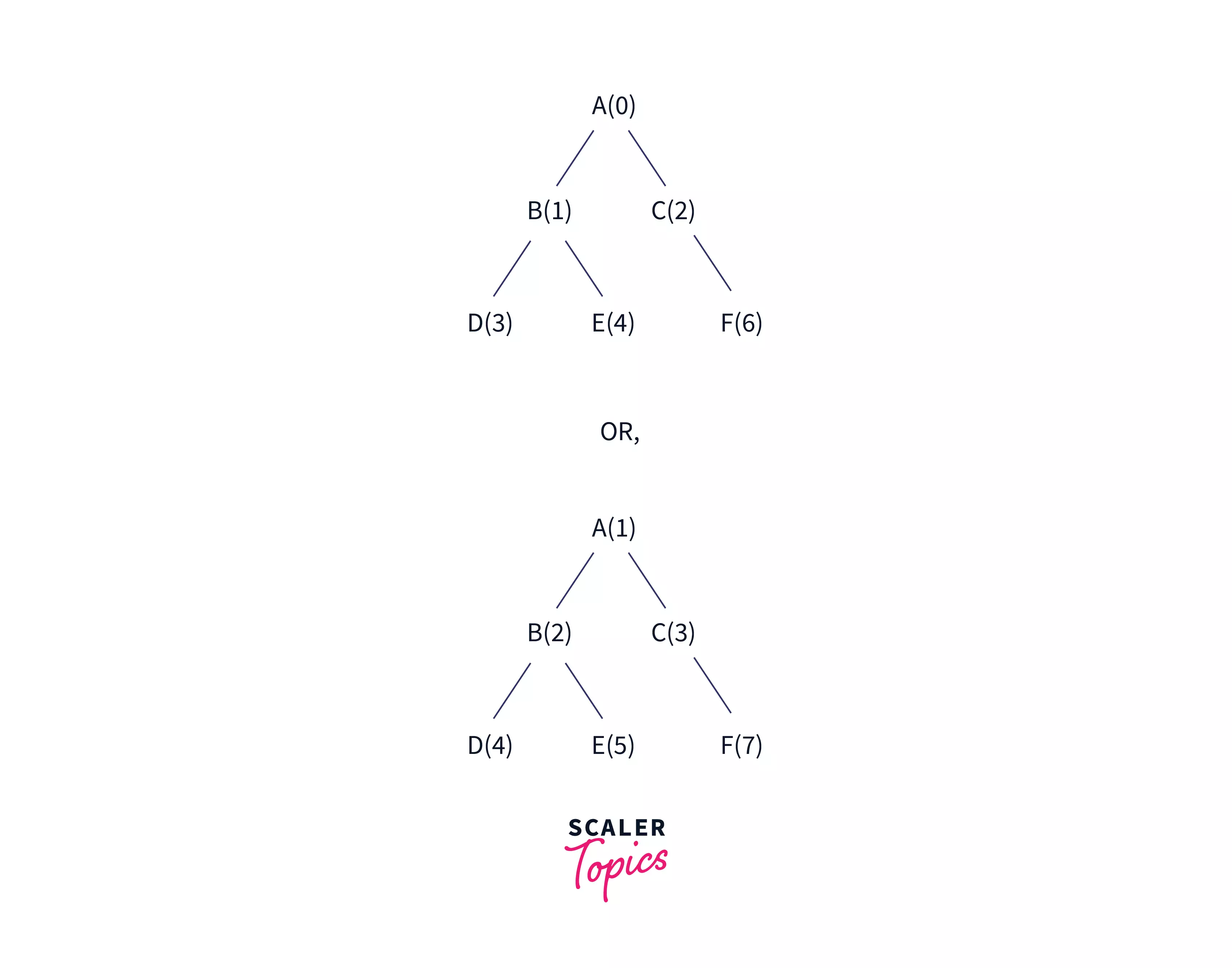
Case 1: If we consider the 0 to n-1 representation: Let the index of a parent be I. Then the index of the left child is 2 * I + 1 and the index of the right child is 2 * I + 2.

Case 2: If we consider the 1 to n representation: Let the index of a node in a binary tree be I. Then the index of the left successor is 2 * I and the index of the right successor is 2 * I + 1. The index of the prdecessor is I/2.

If the root is indexed at one, the predecessor is assigned half of the number assigned to the node. The left successor of the node is twice that of the index of the node and the right successor is at one more than twice of its predecessor.

For a binary tree of n nodes, the minimum length of the array should be n for it to be a complete binary tree and the $2^n - 1$ for a skewed binary tree.

To know more about types of binary trees, you can refer to our article.

Example:

Output:

In the above example, we have considered the indexing to be from 0 to n-1. The next step involves defining the array that stores the data of the binary tree. This is a limitation of the array representation as the size of the array has to be fixed at the time of creation. We define three methods - Root, set_Left, and set_Right to assign values to the root, left and right child of the parent passed parameter. The methods take the key and the index of the parent as the parameter. If the parent does not exist, i.e., if the value at the given index is null, it prints "No parent found for child". Otherwise, it sets the key value at the required position. The function print_Tree prints the elements of the array sequentially representing the null nodes by a dash (-).

In the main function defined in the tree class, we first define an object of the class Array_imp. All the elements are pushed into the array one by one. The print_Tree function prints the elements of the tree level by level.

Applications of Binary Tree

• The trie data structure which is a variation of a Binary tree is used to store the location of routers based on their IP address and group them according to their address in a single subtree.
• Use for classification purposes in supervised machine learning algorithms. A binary tree is used in the decision-making process of a supervised machine learning algorithm. It begins with the root node, storing the conditions or dataset features at the internal nodes. The leaf nodes display the outcome of the decision.
• Used in sorting algorithms as the inorder traversal of binary search tree gives us the sorted order of elements.
• B-Trees, a variation of Binary trees are used in database indexing to sort data for more optimized searching, insertion, and deletion.
• Used to compress data by Huffman coding. It is a data compression algorithm that builds a binary tree by inserting the encoding of characters in the nodes depending on their frequency.