Bubble Sort in Java

Introduction to Bubble Sort in Java

We all have seen leaderboards, and we often observe that the data on the board are arranged in decreasing order of performance, keeping the best performer on top. Have you ever wondered how such a large amount of data get arranged? This all is done using a process of ordering data in a certain fashion termed sorting. Bubble sort is a technique that can sort the data for us. It can sort the data in any order, be it increasing or decreasing.

The main idea of bubble sort is to traverse the given array multiple times, comparing two adjacent elements and swapping them if they are not in the desired sorting order until the array is sorted. It is called bubble sort because at the end of each pass, largest or smallest(based upon the desired sorting order) is pushed bubbled to its desired position in sorted order.

Algorithm of Bubble Sort

Using the bubble sort algorithm, we can sort an unsorted array A of size N in increasing order in three simple steps. Traverse the array N-1 times and follow the steps.

1. Starting with the very first element of the array, compare the current element with the next consecutive element.
2. if the current element A[i] is greater than the next element A[i+1], swap them and move to the next element and repeat step 2.
3. else move to the next element and repeat step 2.

One element of the unsorted array is pushed to its appropriate position in sorted order after one pass, meaning:

• After the 0th pass, the array's largest element will be shifted to the rightmost place (to its correct place in sorted order), leaving us with N-1 elements to sort.
• After the 1st pass, the largest element of the unsorted array will be pushed to its proper location, leaving us with N-2 elements to arrange.
• After the ith pass, we'll have N-i-1 elements to sort, which means after N-1 iterations, we will be left with 0 elements to sort. Hence, we need max N-1 passes to sort the array.
• We have N-i (index 0 to index N-i-1) elements to compare in the 'ith' pass, and we only need to iterate until the second last element of N-i elements because we will be comparing the current element to the next.

In the example below, we'll see it more clearly.

Pseudocode of Bubble Sort in Java

Since we know that the Bubble sort algorithm sorts the array in N-1 passes, we will use one (outer) for loop for N-1 passes indexed from 0 to N-2. And to be able to traverse the array to compare and swap the elements, we will use another for loop nested into it. Finally, we will use logical If to compare the adjacent elements. In other words

• Outer for loop is used for N-1 passes, making the algorithm traverse the array N-1 times.
• The inner for loop is responsible for visiting the array of elements. This goes from 0 to N-PassNum-2 because, in the ith pass (0 <= i <=N-2), we need to compare N-i elements, indexed from 0 to N-i-1 in such a manner that we always compare the current element with next consecutive element. It means if the current element is at index N-i-2 (in the ith pass), then we will be comparing it with the next consecutive element indexed at N-i-1.

Sort An Array Using Bubble sort

Let's take an unsorted array A = [7,11,9,2,4] containing five elements. We will sort it in increasing order using the Bubble sort algorithm. Our desired output is [2,4,7,9,11].

To sort the array, we will need a total of 4 (N-1) passes indexed from 0 to 3.

Let's walk through the algorithm step by step.

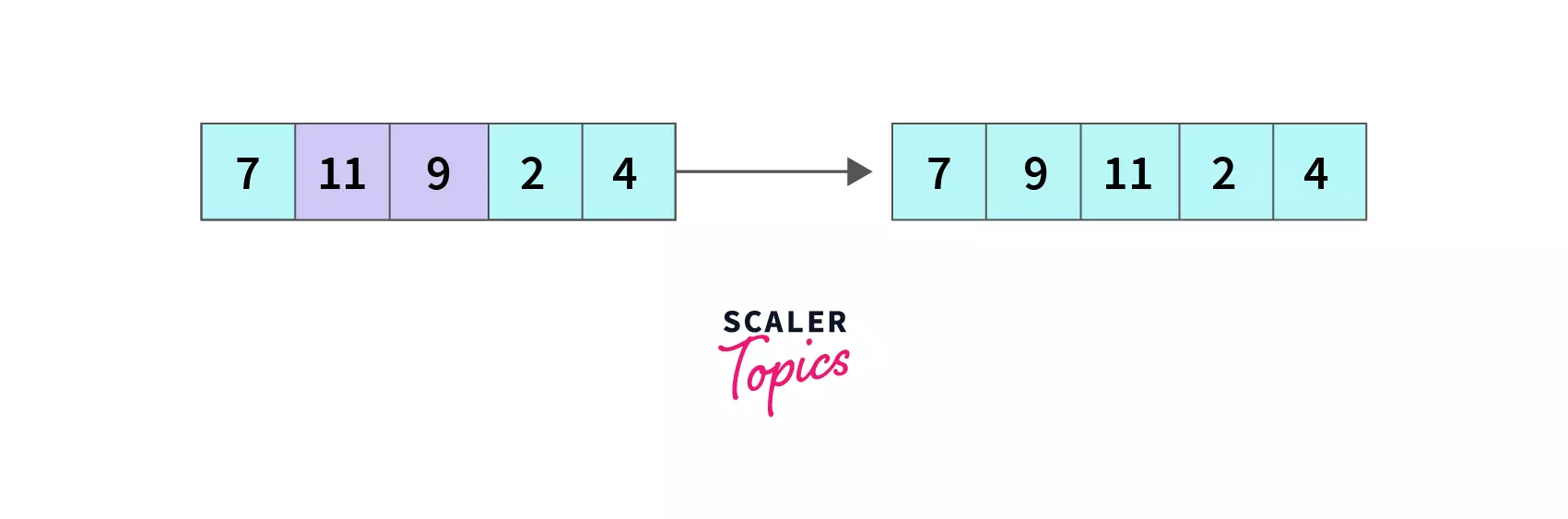
First pass (PassNum = 0)

• index = 0, we compare A[0] and A[1] since 7 < 11, so there is no change in the array, and we move to the next element.

  • 

• index = 1, A[1] which is 11 is greater than A[2] which is 9 so we swap A[1] and A[2], the array becomes [7,9,11,2,4] and we move to the next element.

  • 

• index = 2, compare A[2] with A[3], 11 > 2 so A[2] and A[3] are swapped and the array becomes [7,9,2,11,4] and we move to next element.

  • 

• index = 3, compare A[3] with A[4], 11 > 4 so A[3] and A[4] switch their places resulting the array as [7,9,2,4,11].

  • 

  End of the first pass, we have compared all 5 elements in pairs by iterating till the second last element, and as a result, 11 is pushed to its desired position, and the array is [7,9,2,4,11] now.

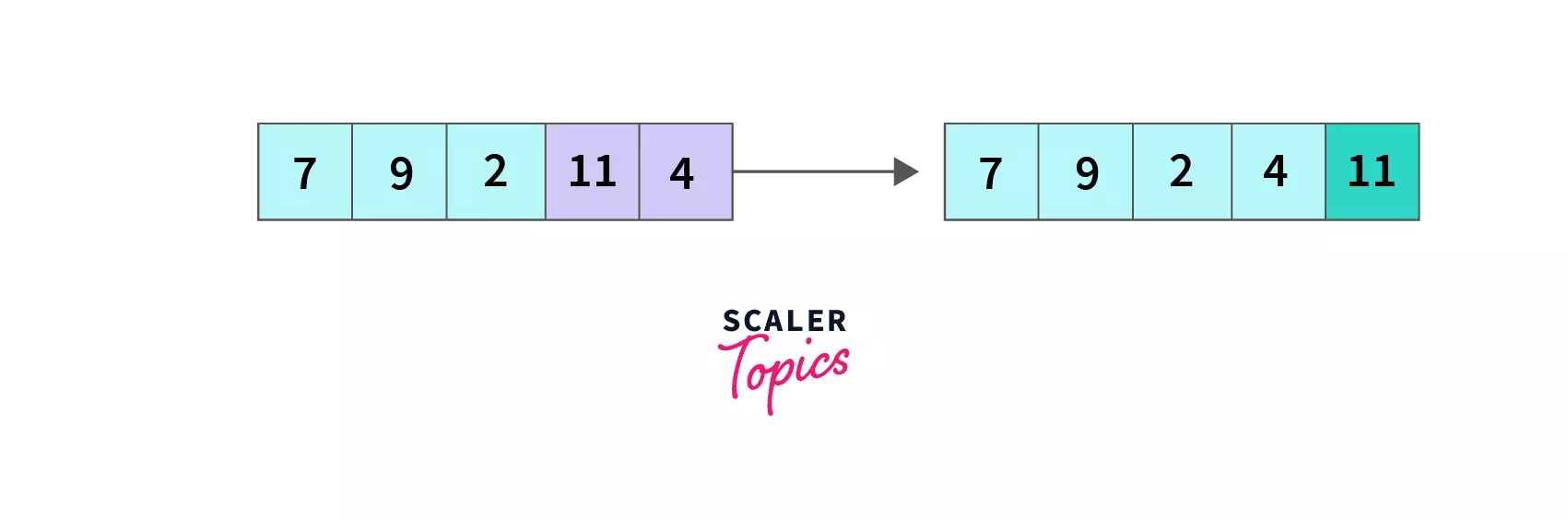
Second pass (PassNum = 1)

• index = 0, we compare A[0] and A[1], since 7 < 9, so no change in the array, we move to the next element.

  • 

• index = 1, A[1] is 9 is greater than A[2] is 2 so we swap A[1] and A[2], the array becomes [7,2,9,4,11] and we move to the next element.

  • 

• index = 2, compare A[2] with A[3], 9 > 4 so A[2] and A[3] are swapped and the array becomes [7,2,4,9,11].

  • 

  At the end the of the second pass, we have compared all 4 remaining unsorted elements (11 were sorted in the first pass) in pair by iterating till the second last element, and as a result, 9 (largest of the remaining 4 elements) is pushed to its desired position, and the array is [7,2,4,9,11] now.

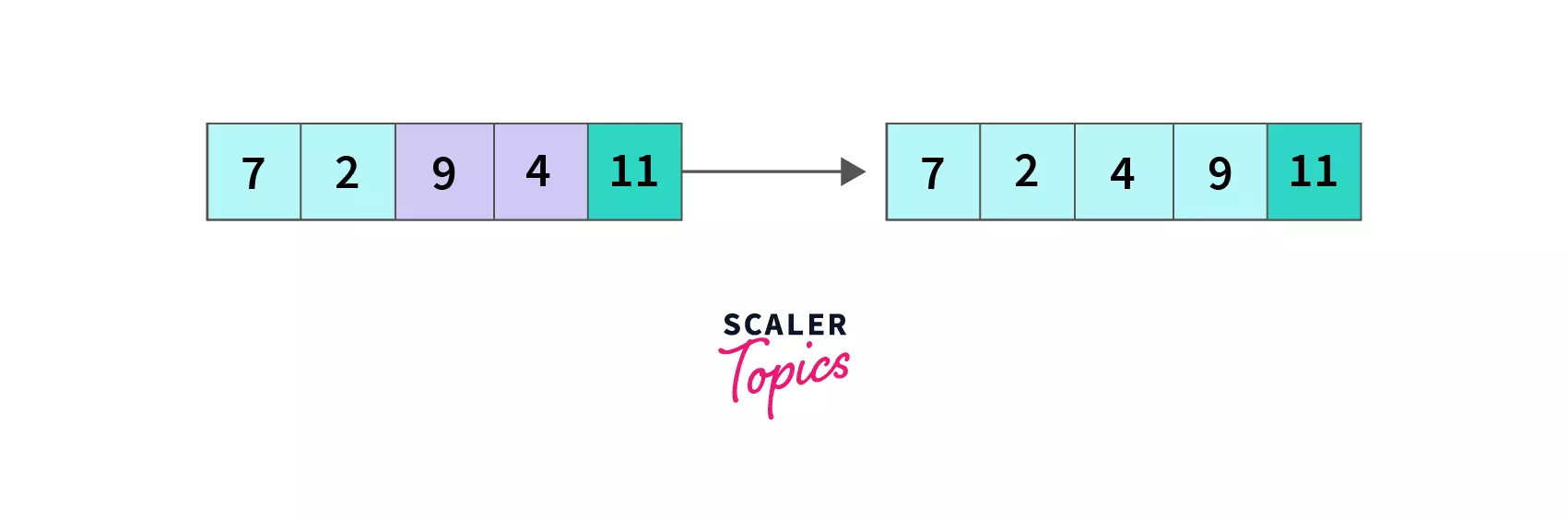
Third pass (PassNum = 2)

• index = 0, A[0] which is 7 is greater than A[1] that is 2 so we swap A[0] and A[1], the array becomes [2,7,4,9,11] and we move to the next element.

  • 

• index = 1, compare A[1] with A[2], 7 > 4 so A[2] and A[3] are swapped and the array becomes [2,4,7,9,11].

  • 

  End of the third pass, we have compared all 3 remaining unsorted elements (9 and 11 were sorted earlier) in pairs by iterating till the second last element, and as a result, 7 (largest of the remaining 3 elements) is pushed to its desired position and the array is [2,4,7,9,11] now.

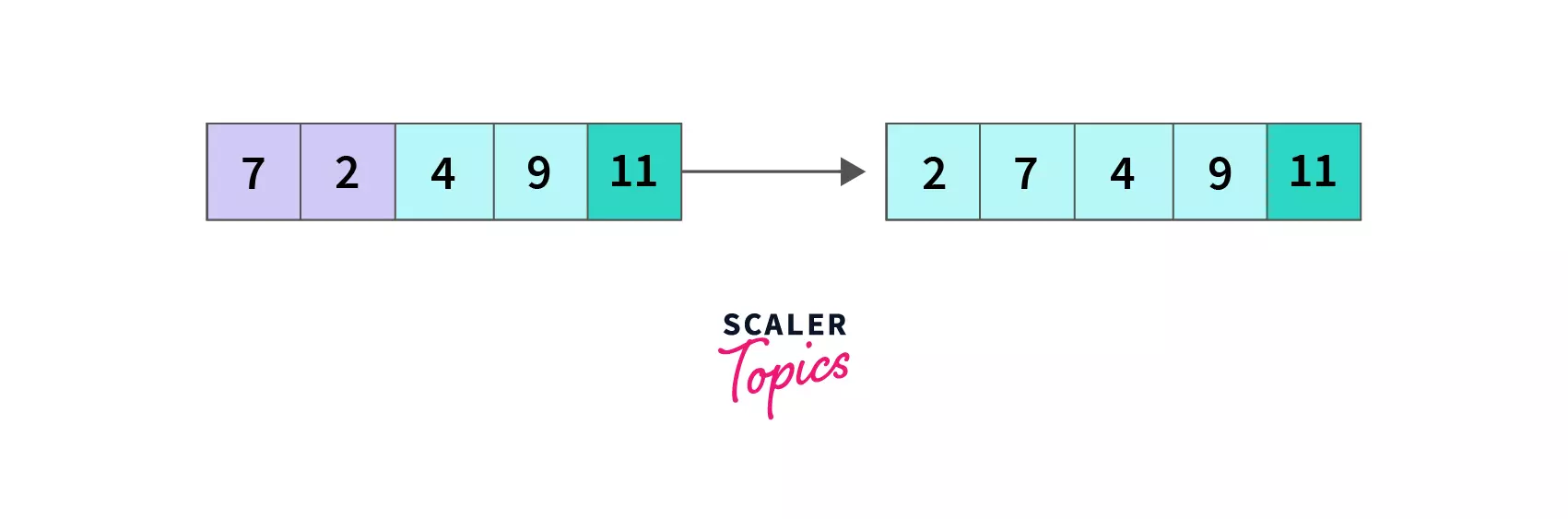
Fourth pass (PassNum = 3)

• index = 0, we compare A[0] and A[1], since 2 < 4, so no change in the array.

  • 

  End of the fourth pass, even though the array was sorted in the third pass, we don't have a way to check if it's sorted and end the loop. As a result, we had to complete the maximum number of N-1 passes possible.

Implementing Bubble Sort in Java

Bubble Sort Java Implementation in Ascending Order

• Here, we will implement the bubble sort function, which will take an unsorted integer array and an integer representing the size of the array as input and will sort the original array in ascending order.
• This function requires two for loops, one nested into another. The outer for loop is N-1 passes.
• For each pass, we will traverse the remaining unsorted elements, using the inner for loop. We will compare the current element with the next consecutive element using the logical if condition.
• Once the if condition is satisfied (A[index] > A[index+1]), we swap the values.
• To swap the values, we first save the value of the current element in a separate variable called swap, then assign the value of the next consecutive element to the current element, and then update the value of the next element with the value saved in the swap variable.

Bubble Sort Java Implementation in Descending Order

Attempt to move the smallest element to the rightmost index, which means that if the current element is smaller than the next element, the two elements should be swapped.

Optimized Bubble Sort Implementation in Java

Let's try sorting another array [8, 2, 6, 5, 9] in increasing order, using bubble sort, following a similar approach to the preceding example. Since the array size is 5, we will need 4 passes.

• First pass keep comparing and swapping as we did earlier, at the end of a pass, the array becomes [2, 6, 5, 8, 9].
• Second pass will change the array to [2, 5, 6, 8, 9].
• Third pass causes no change in the array because it was stored in the previous pass hance the elements are in order, and no swapping operation occurs.
• Fourth pass no change in the array.

The array was sorted after the second pass in this example, but we still had to go through the third and fourth passes. Consider what happens if the input array is already sorted: there will be no swapping (since neighbouring elements are always in the appropriate order), but we will have to repeat the procedure for all N-1 passes.

In such circumstances, if we can figure out if the array is sorted or not and then stop the execution if it is, we can avoid those unnecessary passes.

Close examination of the preceding example reveals that if no swapping occurs in a given pass, this indicates that the array has gotten sorted, and we should omit the remaining passes.

For this, we can have a flag variable that is set to False before each pass and is made True when swapping is performed. If this flag is False at the end of any pass, meaning the array got sorted and we can terminate the further execution of the code.

Below, we have coded the optimized bubble sort in Java to sort the array in increasing order. We employ two for loops, one nested into the other, similar to the original Bubble sort. The outer for loop makes us repeat the procedure N-1 times, while the inner for loop traverses the array.

• We used a boolean variable called isSwapped in each iteration, initially set to false.
• And traverse the array by comparing adjacent elements. If the current element is greater than the next consecutive element, then we mark isSwapped True and swap those elements.
• After traversing the array in every pass, we check if isSwapped is False or not; if it's false, meaning there was no swapping in that pass, indicating the sorted array, and we break the outer loop, which stops the execution of the code.

Time and Space Complexity

We must perform N-1 iterations in the bubble sort algorithm. Each iteration includes a comparison and, if necessary, swapping. The first iteration compares N-1 elements in an array of size N. N-2 comparisons are performed in the second iteration. As a result, the total number of comparisons will be as follows:

which is nearly $N^2$, therefore, the average case time complexity of the bubble sort algorithm is $O(N^2$).

Worst Case Time Complexity of Bubble Sort

The worst-case scenario occurs when we sort in ascending order and the array is ordered in descending order. Since all the elements are in the opposite order, therefore, there will be swapping in each pass, in this case, all N-1 passes are required to sort the array, which required total N(N-1)/2 comparison operations. Hence, the worst-case complexity, in this case, will be $O(N^2)$.

Best Case Time Complexity of Bubble Sort

When we sort in ascending order, and the array is already ordered in ascending order, we have the best-case scenario because the array is already ordered, and our flag variable can break the loop in one pass. The best-case complexity, in this case, will be O(N).

Space Complexity of Bubble Sort in Java

Because we don't need any additional space to sort the array with bubble sort, the space complexity is O(1).

Benefits of Bubble Sort in Java

• The bubble sort's main advantage is that it is widely used and simple to implement.
• In its best-case scenario, which is to check whether the array is already sorted, the optimized algorithm is extremely efficient.
• Bubble sort is an in-place sorting technique, which means it does not require additional space to sort the array, it can modify the original array.

FAQs

1. What is a sorting algorithm? List down the Sorting Algorithms in Java. A sorting algorithm is a method for sorting elements into a predetermined order, such as alphabetical, highest-to-lowest value, or lowest-to-highest value.

   Sorting algorithms in Java are:-

   • Quick Sort
   • Merge Sort
   • Insertion Sort
   • Selection Sort
   • Heap Sort
   • Radix Sort
   • Bucket Sort

2. What is the best Sorting Algorithm in Java? The best sorting algorithm is Merge sort, which has a time complexity of O(NlogN). However, there is no such comparison; different sorting algorithms may perform best in different scenarios.

3. When Can We Use Bubble Sort? Bubble sort is a quick way to see if an array is sorted or not. It's also useful for sorting small-size arrays.

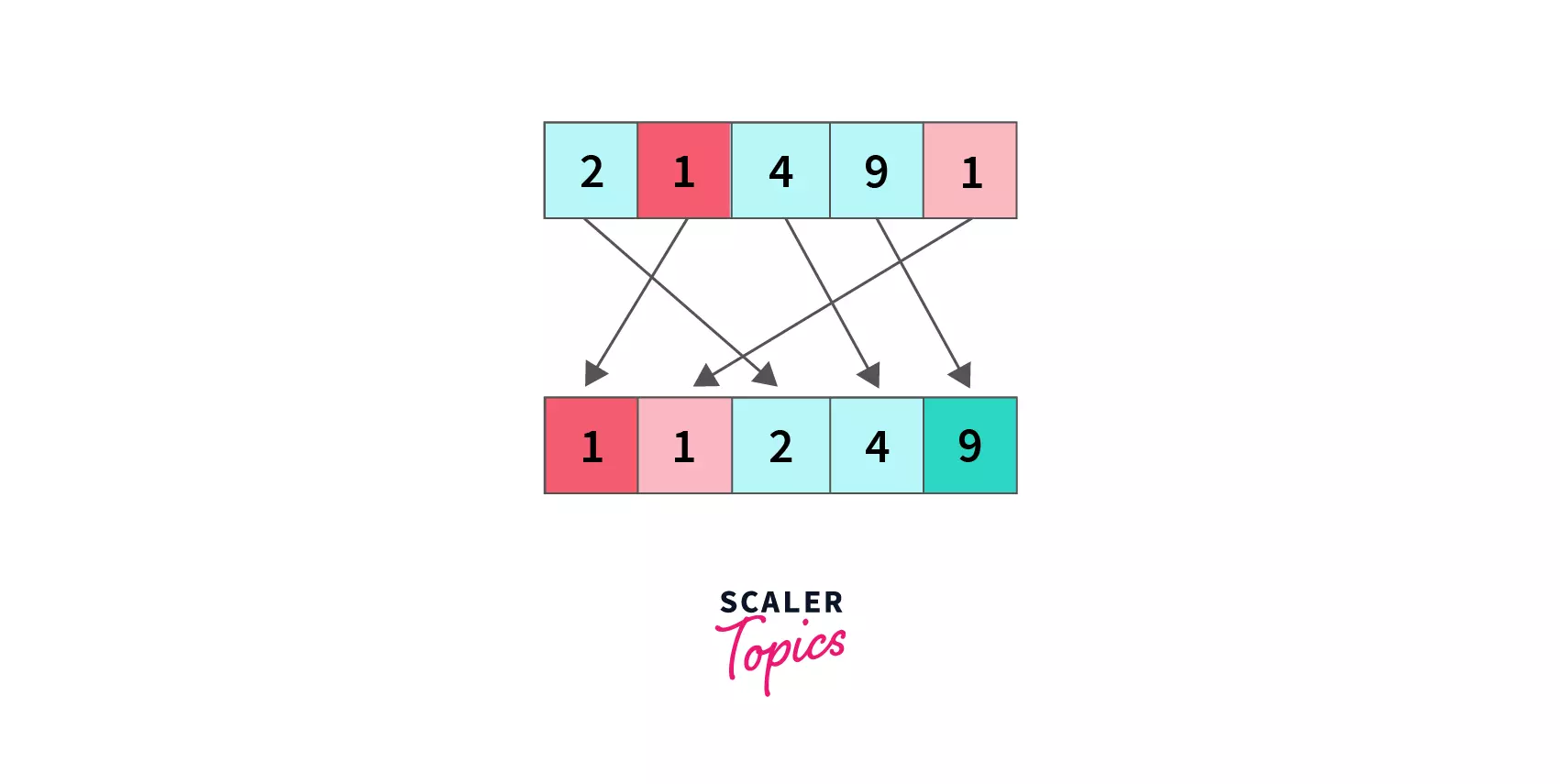
4. Is Bubble Sort Stable Sorting Algorithm?

   Stable algorithms are those that preserve the relative order of equal elements even after sorting.

   As we can see in the example below, 1, which is at the rightmost index initially, will always be on the right of 1 on its left, even after the sorting is done. Hence bubble sort is a stable sorting algorithm.

   • 

5. What are the disadvantages of bubble sort in Java?

   The main downside of the bubble sort approach is the amount of time it takes. With an $O(N^2)$ running time, it is inefficient for large data sets. As the number of elements in the array grows, so does the average time complexity of the Bubble sort algorithm.