Bubble Sort in JavaScript
Learn via video course

Overview
Bubble sort is a sorting algorithm that compares adjacent elements and swaps them if they do not follow the desired order. This algorithm is stable and follows in-place sorting. Easy-to-understand and implement, bubble sort in JavaScript takes O(n^2) time complexity to sort and is not the most optimal sorting algorithm possible.
Scope of Article
- In this article, you'll understand the bubble sort algorithm and see how it is implemented in the case of numbers.
- You'll understand the logic and see the dry run using an example.
- This article explains the loopholes in the bubble sort algorithm and puts light on the areas of improvement of the algorithm.
- This follows by the optimized solution of this algorithm.
- The best-case, average, and worst-case time complexity are discussed in detail, along with its space complexity.
- Alternatives to the bubble sort algorithm are explained.
Introduction - Sorting, bubble sort
Sorting stands for arranging elements in a certain order. For example, arranging numbers in ascending or descending order or arranging strings in alphabetical order. Bubble sort is a way of sorting elements by comparing each adjacent element and swapping them if they are out of order. Let us look at the bubble sort in detail in the next section.

How does the Bubble sort Algorithm Work?
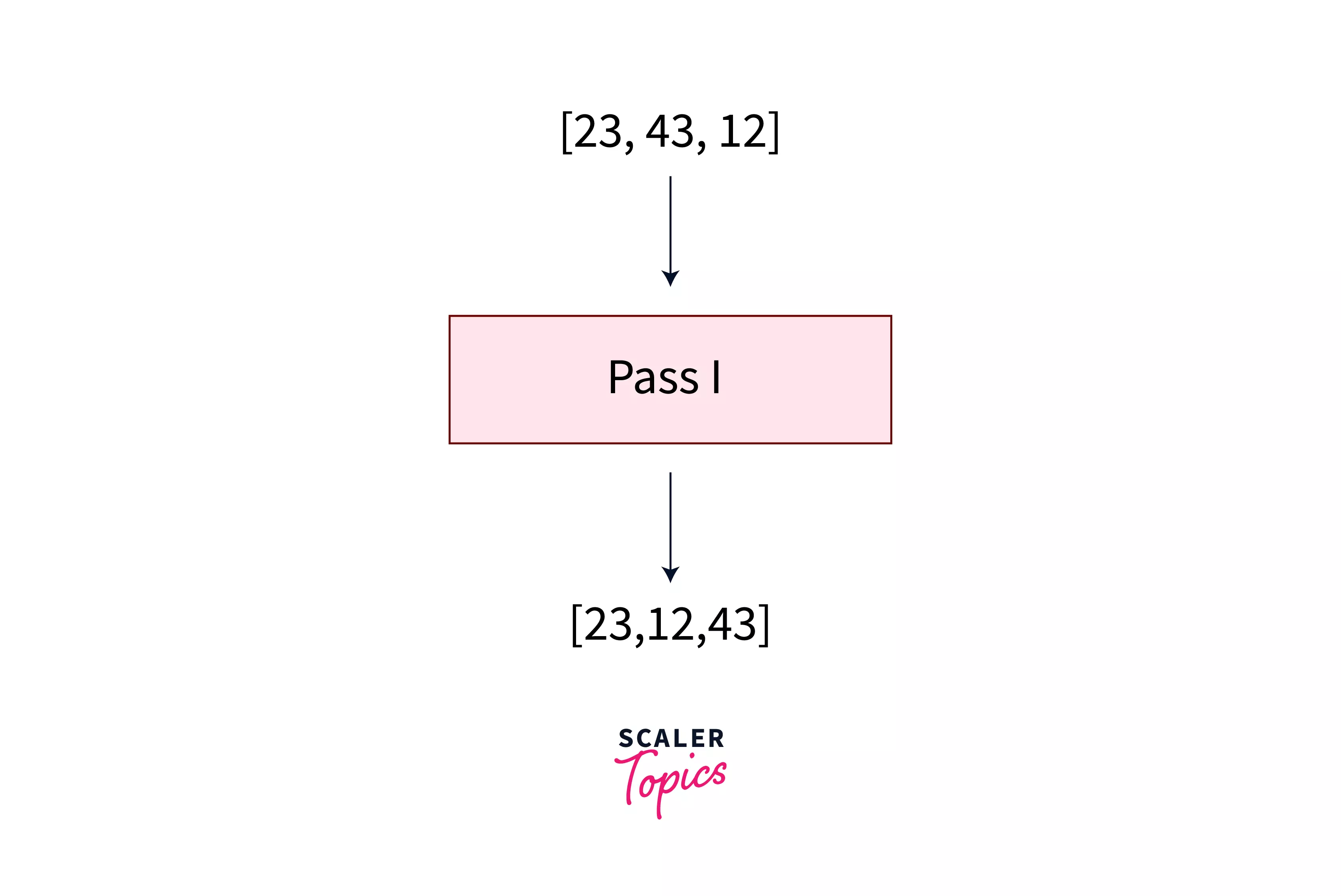
Let us take an example of numbers. Bubble sort in JavaScript works by comparing each adjacent number and swapping them if the numbers are not in the required order. Consider the array [23, 43, 12], and we want to sort the numbers in ascending order.
Pass I:
-
Compare - 23 and 43. We do not need to swap them since they are in the required order, i.e., ascending. Array - [23, 43, 12]
-
Now, compare - 43 and 12. Since the first number is greater than the second one, we will have to swap them, and hence they become - 12 and 43. Array - [23, 12, 43]
This was the first pass. This ensures that the largest number is placed on the last index of the array. If we continue doing this for each number inside a loop, we'll finally get the required numbers in the ascending order.
Pass II:
- Compare - 23 and 12. Since the first number is greater than the second one, we will have to swap them, and hence they become - 12 and 23. Array - [12, 23, 43]
Note: No need to compare the last element now because the last one already came to its correct position after the first pass.

Hence, bubble sort in JavaScript primarily works by comparing each adjacent number and swapping them if they are out of the required order, else leaving them as it is.
Bubble Sort logic
Now, let us look at the bubble sort algorithm in more detail:
Consider the array - [23, 43, 12, 56, 35], and order be ascending order. Let us start by comparing each element and swapping the second element is greater than the first one.
Pass 0:
Let i be the pass/loop Number Let n be the total array length
- We will make (n-i-1) = (5-0-1) = 4 comparisons in the zeroth pass.
- After the zeroth pass, the largest element reaches the last position in the array.
- Part of the array [0:3] is to be sorted in the next pass. The last element needs no comparison.

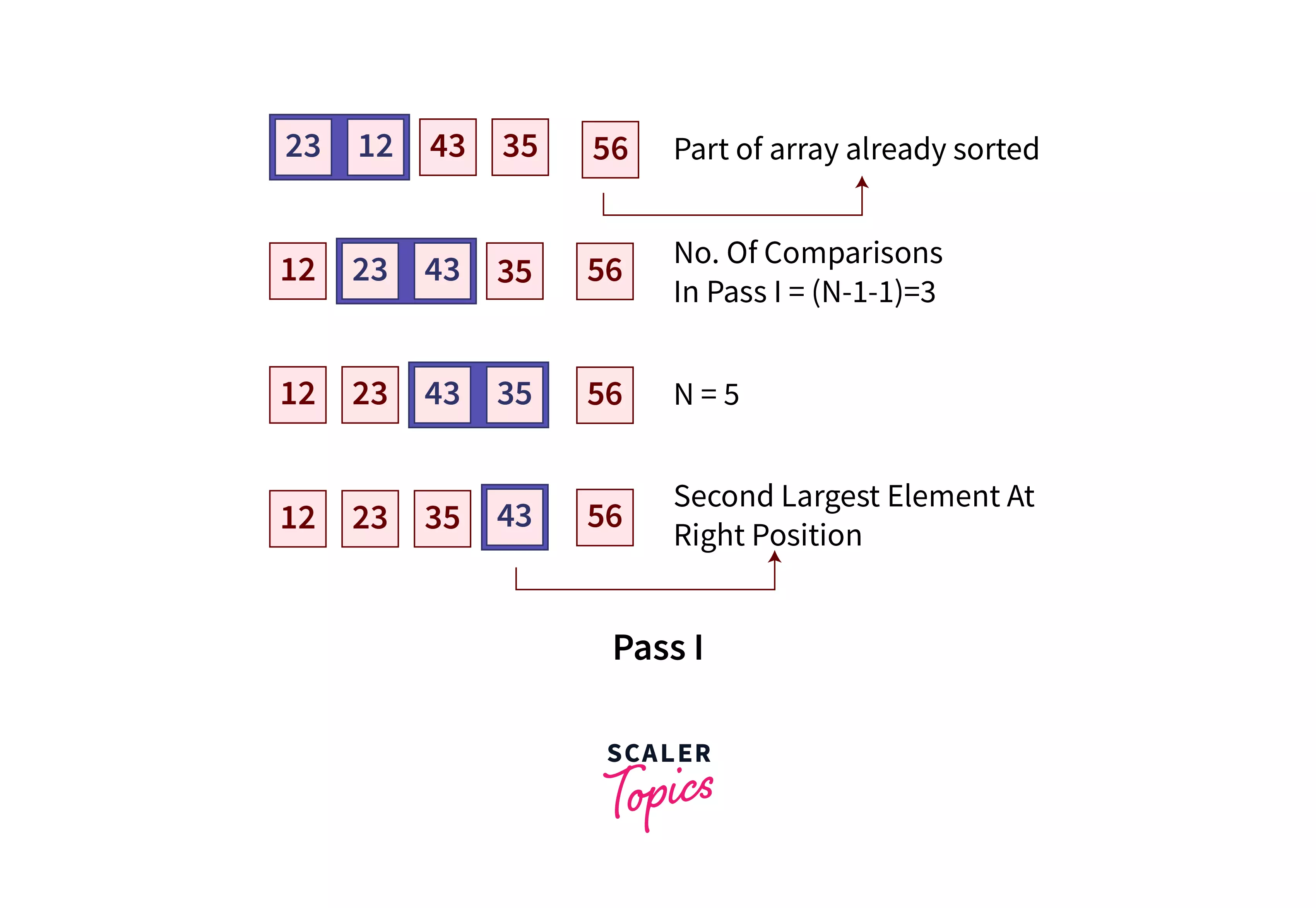
Pass I:
- The last i elements are already sorted. For Pass I, i=1. Rest 4 elements are to be sorted.
- We will make (n-i-1) = (5-1-1) =3comparisons in this pass.
- After this loop, the second largest element reaches the second last position in the array.
- Now, the array [0:2] is to be sorted. The last two element needs no comparison.
Pass II:
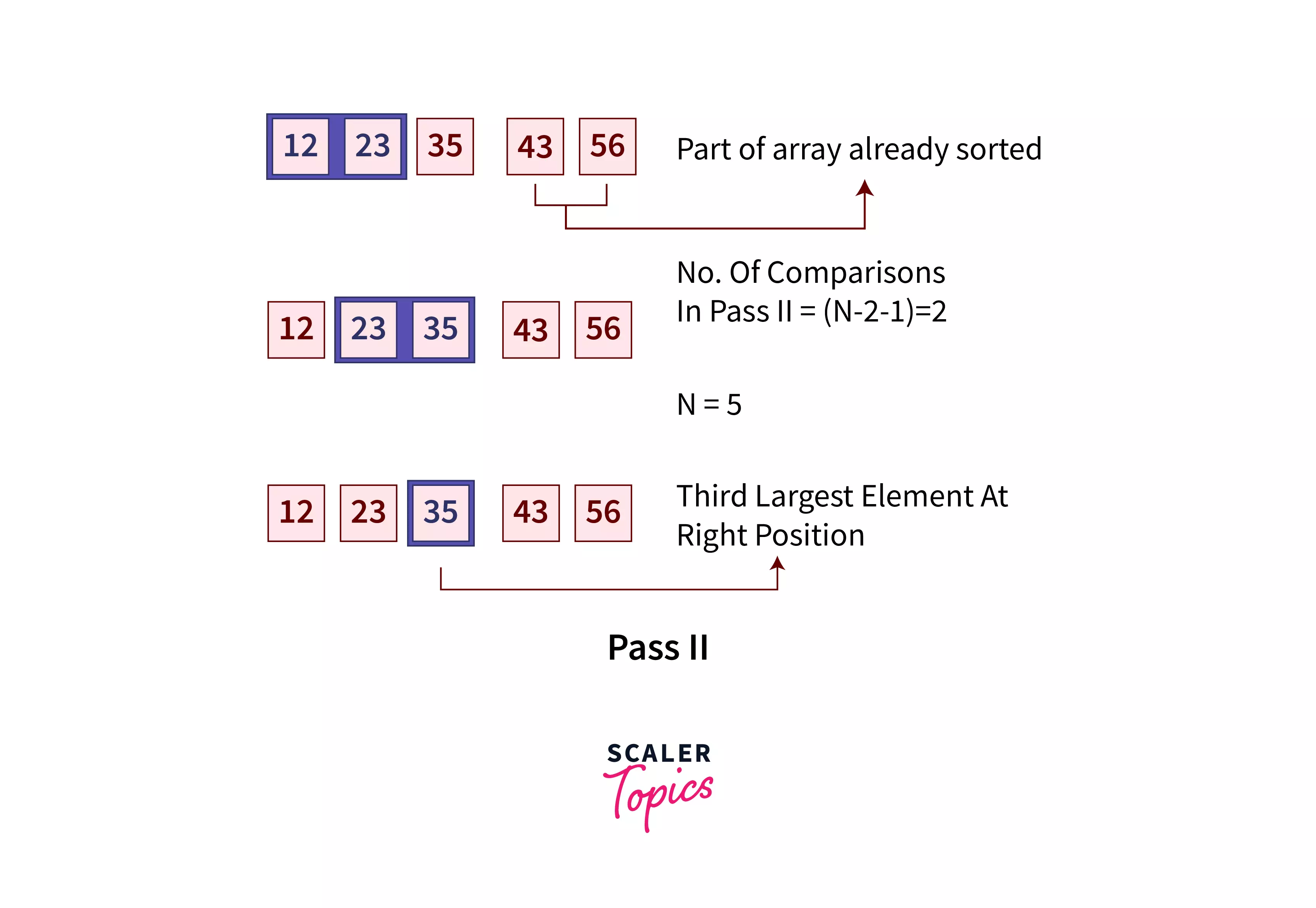
- The last i elements are already sorted. For Pass II, i=2. The first 3 elements are to be sorted.
- We will make (n-i-1) = (5-2-1) = 2 comparisons in this pass.
- After this loop, the third-largest element reaches the third last position in the array.
- Now, the array [0:1] is to be sorted. The last three element needs no comparison.
Pass III:
- The last i elements are already sorted. For Pass II, i=3. The first 2 elements are to be sorted.
- We will make (n-i-1) = (5-3-1) = 1 comparisons in this pass.
- After this loop, the fourth largest element reaches the fourth last position in the array.
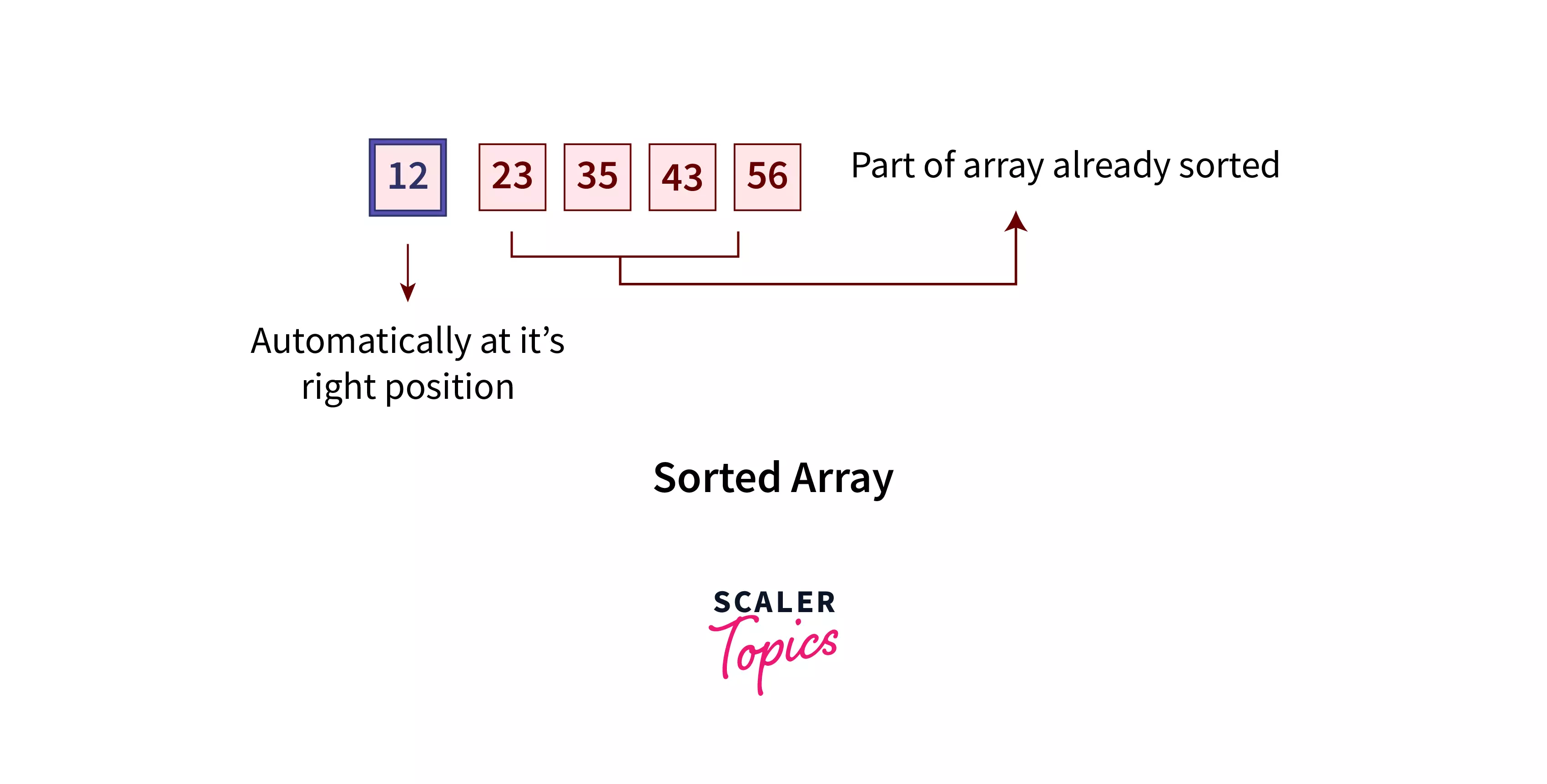
- Now, the array [0:0] is to be sorted. The last four element needs no comparison.

Four elements of the array are already at their correct positions according to the specified order, i.e., ascending. So, the last remaining element is automatically at its correct position. Hence, we get the sorted array.
Points to be noted:
- If arrLength is the number of element in the array, we need to run (arrLength-1) loops, i.e from loop = 0 to loop = 5-1 = 4
Note: Since after each pass/loop, one element comes to its right position, after n-1 passes/loops, n-1 elements will be positioned right. The last one left will automatically be in its right position. So, total (n-1) passes are required to sort the entire array.
- For each loop, we need to perform (arrLength - loopNumber - 1) comparisons.
- After pass/loop - I, one element will be in its right position. Likewise, after nth pass/loop, n elements will be rightly positioned. We do not need to perform comparisons on these rightly positioned elements, i.e. on loopNumber number of elements. In other words, perform comparisons on (arrLength - loopNumber) number of elements.
- For Zero based indexing, loop number starts from 0 to (n-1), no. of comparisons are calculated as (arrLength - loopNumber - 1)
-
For loop 0: No. of comparisons: (5 - 0 - 1) = 4.
-
For loop 1: No. of comparisons: (5 - 1 - 1) = 3.
-
For loop 2: No. of comparisons: (5 - 2 - 1) = 2.
-
For loop 3: No. of comparisons: (5 - 3 - 1) = 1.
- In each comparison, we swap the numbers if the second number is greater than the first number and do not touch the order if they are in the correct order.
- After all the comparisons in the first loop, the largest element will be present at the last array position.
- After all the comparisons in the second loop, the second largest element will be present at the second-largest position, i.e., the last two elements will be sorted.
- This way, after each loop, we start getting the last (loopNumber+1) number of elements in the right position; for example, after pass 0, we have 1 element in its correct position.
- Hence, we get the final sorted array after n-1 loops.
- Did you notice that the last two loops got wasted? This is a loophole in this method. We'll look into an optimized solution that solves this problem in the later section.
Syntax
BubbleSort(array){
arrLength <- array.length
for i -> 0 to arrLength - 1
for j -> 0 to (arrLength - i - 1)
if arr[j] > arr[j + 1]
swap(arr[j], arr[j + 1])
}
Implementation
:::
Optimized Solution
We saw in the above section that the last two loops did nothing. The array was already sorted, but we ran the loop for two more times. This increased the time taken for no reason.
To optimize this approach, we can keep a check on the comparisons in each loop using the flag variable. If no swaps are made during a loop, i.e., all the elements are already sorted, mark flag as true. There is no need for the subsequent loops now. This will optimize our solution.
The syntax for Optimized solution
Implementation
Complexities
Let us discuss bubble sort's worst-case, average-case, and best-case time complexities and its space complexity.
Worst-Case time complexity
Consider the elements of the array are in reversed order. In that case, for all the adjacent elements, we'll have to swap them, and this will be for all the n loops. n comparisons for n loops. Hence, the worst-case complexity becomes -> O(n^2).
Average case time complexity
The average case is somewhere in between the worst-case (sorted in reverse order) and the best-case (almost sorted in the right order). Taking the mean of both, we might need (n/2) passes/loops to sort in the average case.
If the array elements are randomly sorted, this forms our average case, where we might need (n/2) number of loops and n comparisons in each loop. This forms our average-case time complexity of O(n/2 * n) -> O(n^2^)
Best case time complexity
In the best case, the elements of the array are almost sorted. We need to run a single loop, make all the n comparisons, break out of the loops and return the final sorted array because of no swaps.
Since, in this case, only one pass and n comparisons in that pass are made, the best-case time complexity becomes O(n).
Bubble Sort space complexity
During each loop and after every comparison, we swap the array elements if they are out of order. We do not use any new memory location to store the sorted array. The original array is modified.
Also, only three variables, namely i,j (iteration variables), and the flag (check variable), are used. Hence, the space complexity for the bubble sort algorithm becomes - O(1).
Bubble Sort Performance summary table
| Cases | Complexities |
|---|---|
| Best-case Time complexity | O(n) |
| Average-case Time complexity | O(n^2^) |
| Worst-case Time complexity | O(n^2^) |
| Space complexity | O(1) |
When to use Bubble Sort?
Bubble sort in JavaScript is a very easy to understand and simple sorting algorithm but is considerably heavy because of its high worst-case and even best-case time complexity. Many other sorting algorithms are much better than bubble sort, for instance, Merge Sort and Quick Sort.
They take up the worst-case time complexity of O(n*logn), which is better than that of the bubble sort. We can consider using bubble sort in two cases:
- If the length of the array is too small to worry about the performance issues: Bubble sort has a high time complexity, i.e., O(n^2^). If the array is too small, this time, complexity will also come out to be considerably small. Hence, we can use bubble sort for smaller arrays.
- If the array is almost sorted, i.e., the best case: Bubble sort's best-case time complexity is O(n), which is better than the best-case time complexity of even the best sorting algorithms, like merge sort and quick sort, i.e., O(n*logn). Hence, for almost sorted arrays, bubble sort is best suited.
Even for the smaller arrays, insertion sort has proved to be a better algorithm. Hence, you'll probably never use bubble sort in real-life projects.
Alternatives to Bubble sort
There are many alternatives to bubble sort, which work with lesser time complexities. The best sorting algorithms are Merge sort and Quick Sort, which work on divide and conquer and have the worst-case time complexity of O(n*logn), which is way better than the time complexity of bubble sort.
Conclusion
- Bubble sort in JavaScript is used to sort elements of the array in a certain way, for example, numbers in ascending or descending order, strings in alphabetical order, etc.
- Bubble sort works by comparing each adjacent elements of the array and swapping them if the elements are out of order.
- We can optimize the algorithm by keeping track of the swaps made. If inside a loop, no swaps are made, which means the elements are in their correct order, we can break out of the loops and return the sorted array.
