C++ Program to Implement Selection Sort
Learn via video course

Overview
Sorting algorithms are used to sort or arrange a particular array or list in ascending or descending order. Selection sort in C++ is a simple sorting algorithm used to rearrange or sort an unsorted array or list in ascending order by considering a minimum element in each iteration and placing that minimum element in its actual position so that the given array becomes sorted after the iteration.
Scope
In this article, we will learn about the following:
- What is Selection sort, and how it works in C++ along with its implementation?
- Time and Space complexity analysis of selection sort algorithm and its Characteristics.
Each topic is explained and elaborated on using detailed examples wherever necessary.
Introduction to Selection Sort
Before learning about selection sort C++, let's learn a bit about Sorting algorithms. Sorting algorithms are used for rearranging the elements of an unsorted array or list so that all of its elements are either in ascending order or descending order. Different kinds of sorting algorithms exist that do the same thing, such as rearranging the elements but using different techniques.
Types of sorting algorithms are as follows:
- Selection Sort
- Insertion Sort
- Bubble Sort
- Merge Sort
- Quicksort
- Counting Sort
- Radix Sort
- Bucket Sort
- Heap Sort
- Shell Sort
Any of the above-mentioned sorting algorithms can be used to rearrange the elements depending on the requirement. Every sorting algorithm has its efficiency, which is determined by the complexity analysis: time and space complexity.
To learn more about sorting algorithms, refer to the article What is Sorting?.
Let's now discuss the Selection sort C++ algorithm.
Selection sort is a sorting algorithm that uses in-place comparison to rearrange elements in several rounds or iterations. In each round, the algorithm selects the smallest element from the given list or array. It places the smallest element at the beginning of the list by swapping after comparison from every element of the list or array. Therefore, if we have n elements inside an array, it takes (n-1) iterations or rounds to be fully sorted.
In selection sort, the smallest element is initially selected and placed on the first index (0th index). The second smallest element is selected and placed on the second index (1st index), and so on.
How does Selection Sort Work?
The selection sort algorithm works in a way that it divides the list into two different lists, one is the unsorted list, and the other one is the sorted list. The sorted list exists on the left side, and the unsorted list exists on the right side. Initially, the sorted list will be empty, and the unsorted list will be filled with elements.
Let's discuss the actual working of Selection sort in C++ step by step with detailed illustrations:
- STEP 1- First, we have to consider the first element of an array or list as the minimum element.

- STEP 2- Now, we have to compare the first element, the minimum element, with the second element. If the second element is less than the current minimum element, we will consider the second index element as the smallest; otherwise, we will move forward.
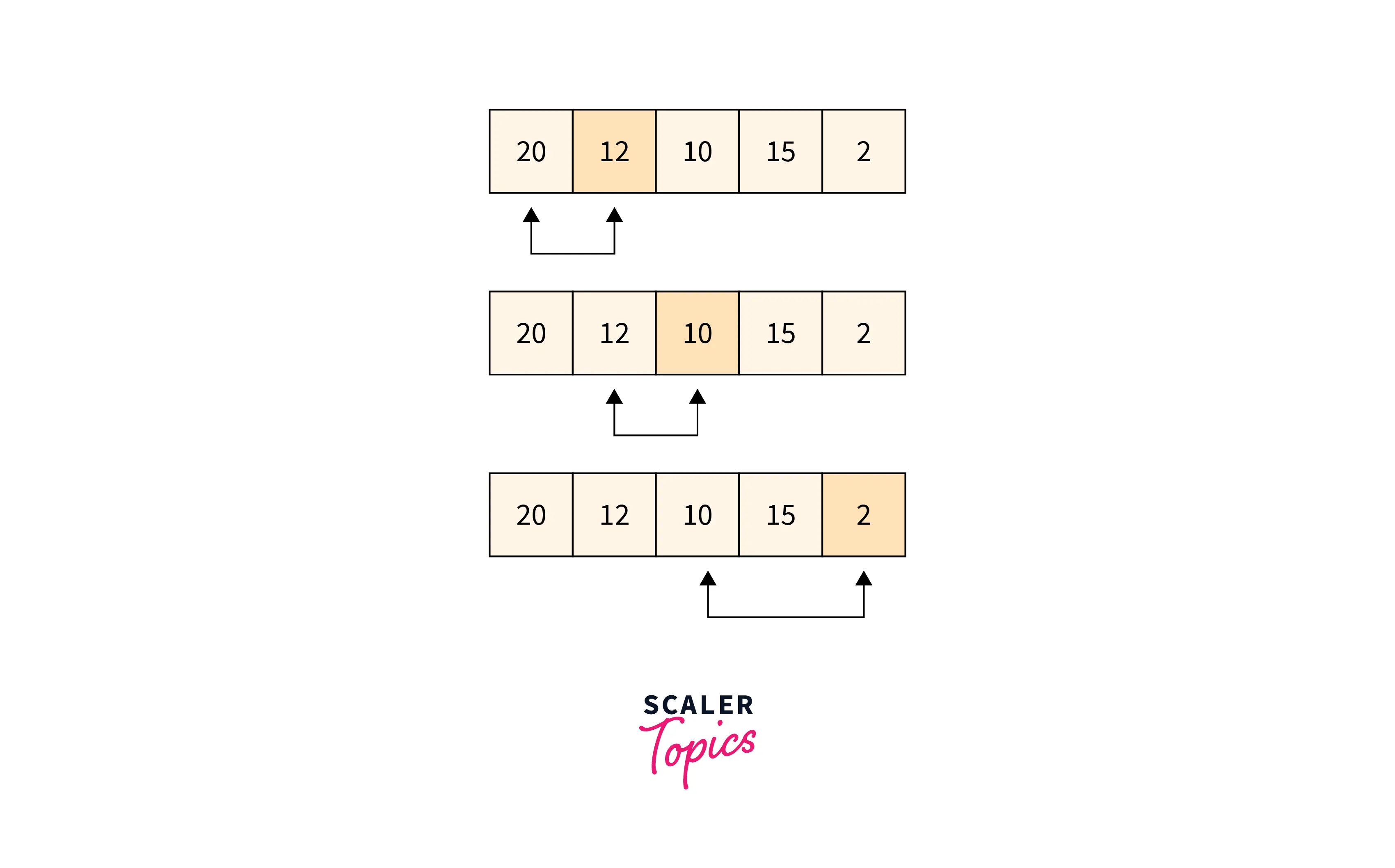
- STEP 3- Again, the same step of comparing the second element, that is, the minimum element, with the third element, and if the third element is lesser than the current minimum element, then we will consider the same element as the minimum element otherwise we will move forward. This process will continue until the last element of the array or list.
- STEP 4- After traversing through the entire array, we will assign the minimum element to the first position of the array, or in other words, we will swap the first element with the first minimum element of the array.
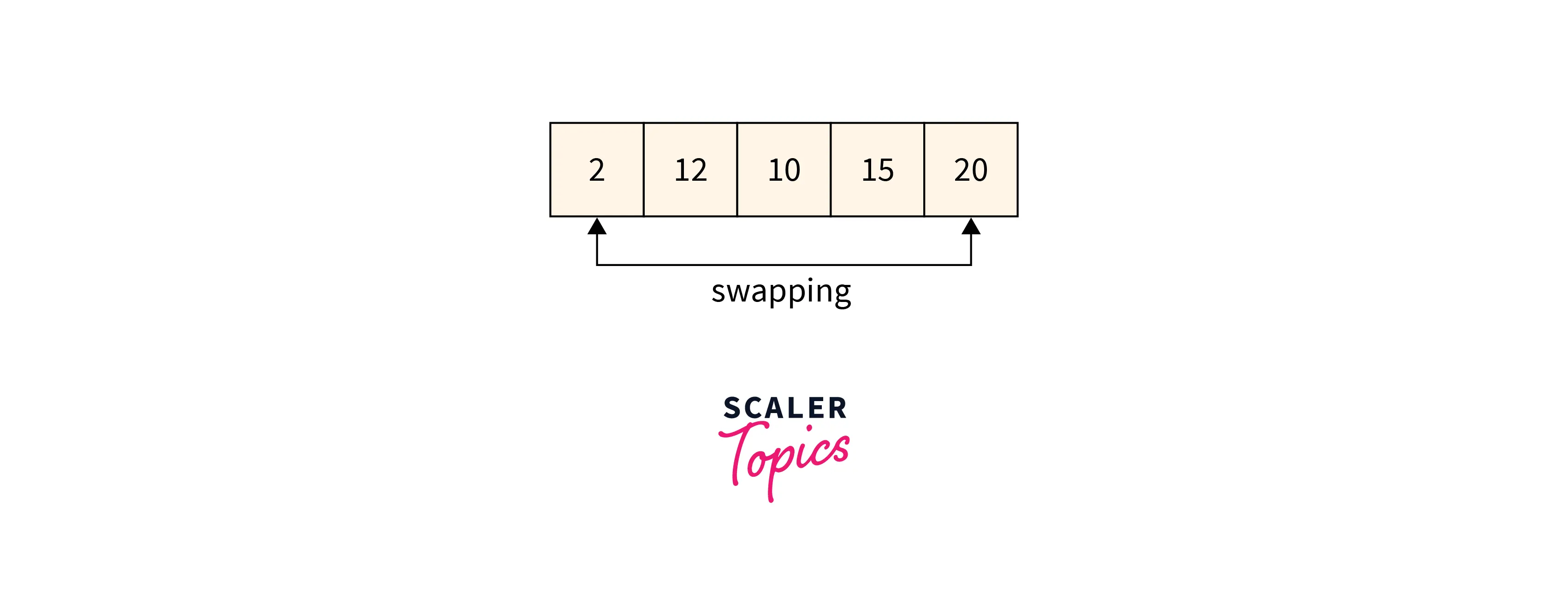
- STEP 5- The indexing always starts from the first unsorted element (Since previous elements are placed at their correct position, they are sorted, and the remaining are unsorted) so that each element of the list can be placed at its correct index. The above step will be repeated until all the elements get placed at their correct position in the list.
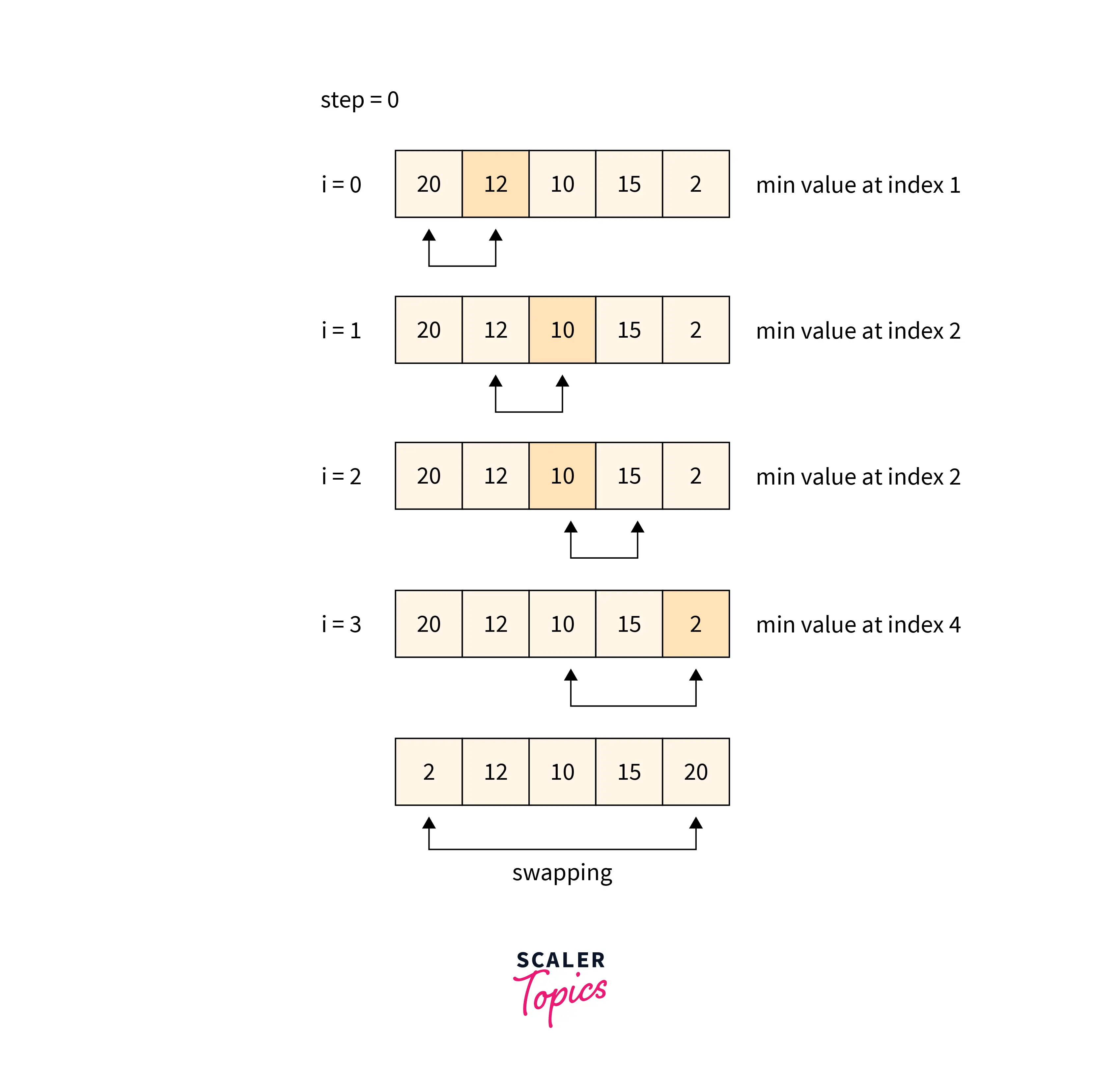
- The above image shows how every element is compared to its adjacent element, and then the smallest element is swapped to the first position.
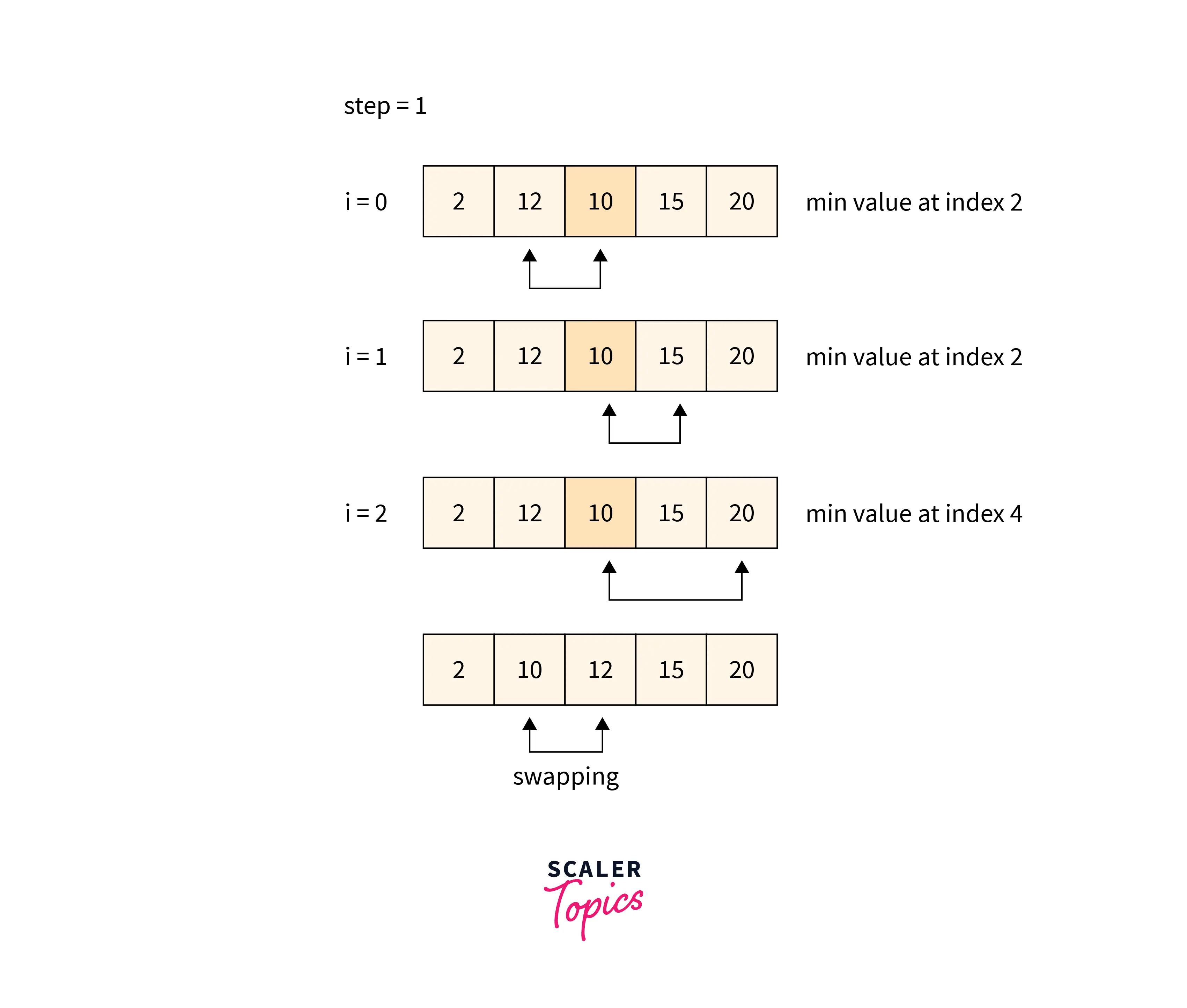
- The above image shows that the iteration starts from the second position, and after comparisons, the second smallest element is swapped into the second position.
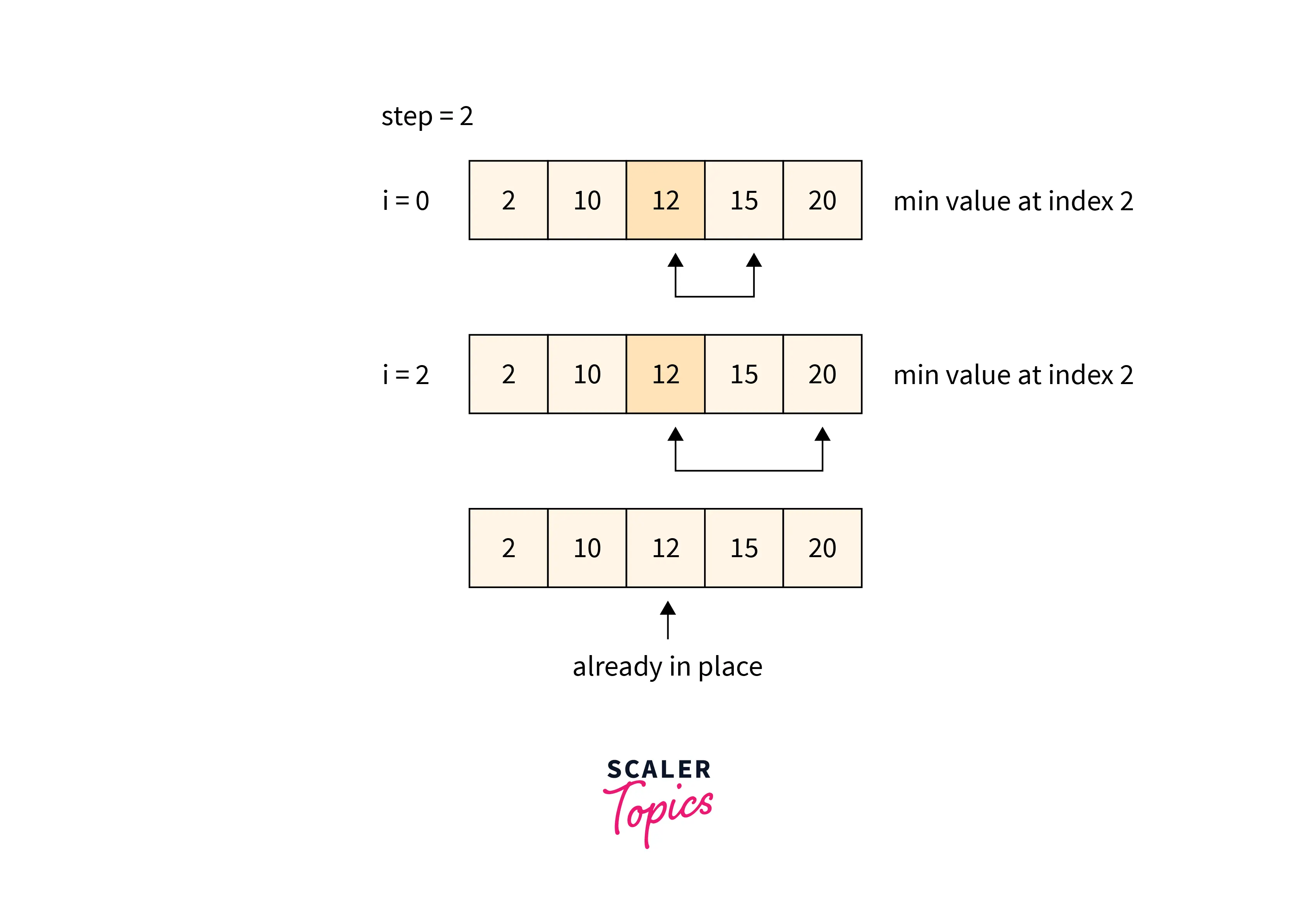
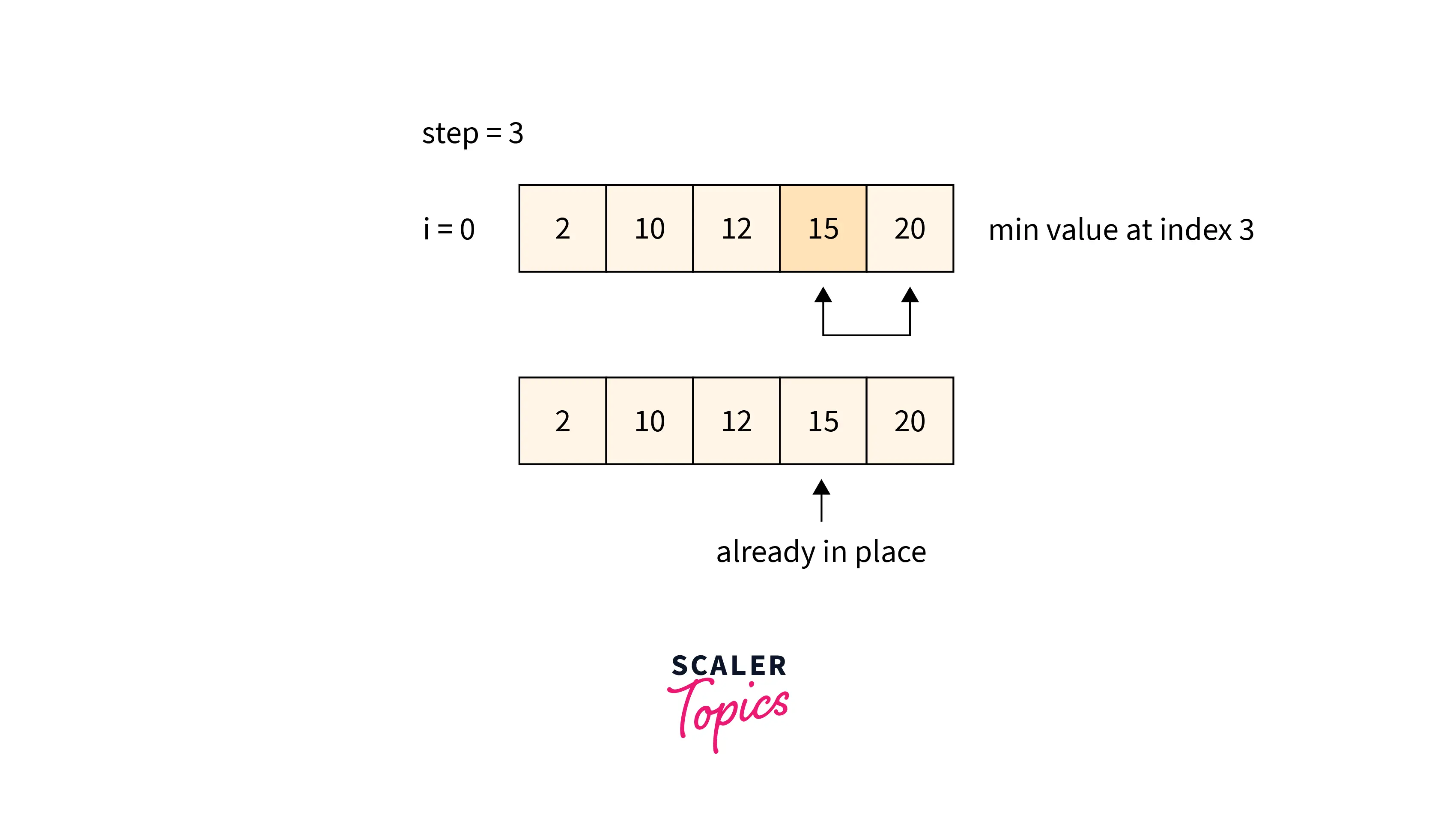
- Similarly, the above two images also show the iterations until sorting the whole array means every element is placed at its correct position.
Selection Sort Algorithm
The Selection sort algorithm consists of the following steps:
- First, we have to initialize the first index as the minimum (indexMin; Here, indexMin represents the current minimum element of the array).
- After that, we traverse the remaining array to find the first minimum element of the array.
- As discussed, if any value is smaller than the current minimum element, we will swap their values. After swapping, we will update indexMin to point to the next element.
- We will repeat all the steps until the entire array becomes sorted.
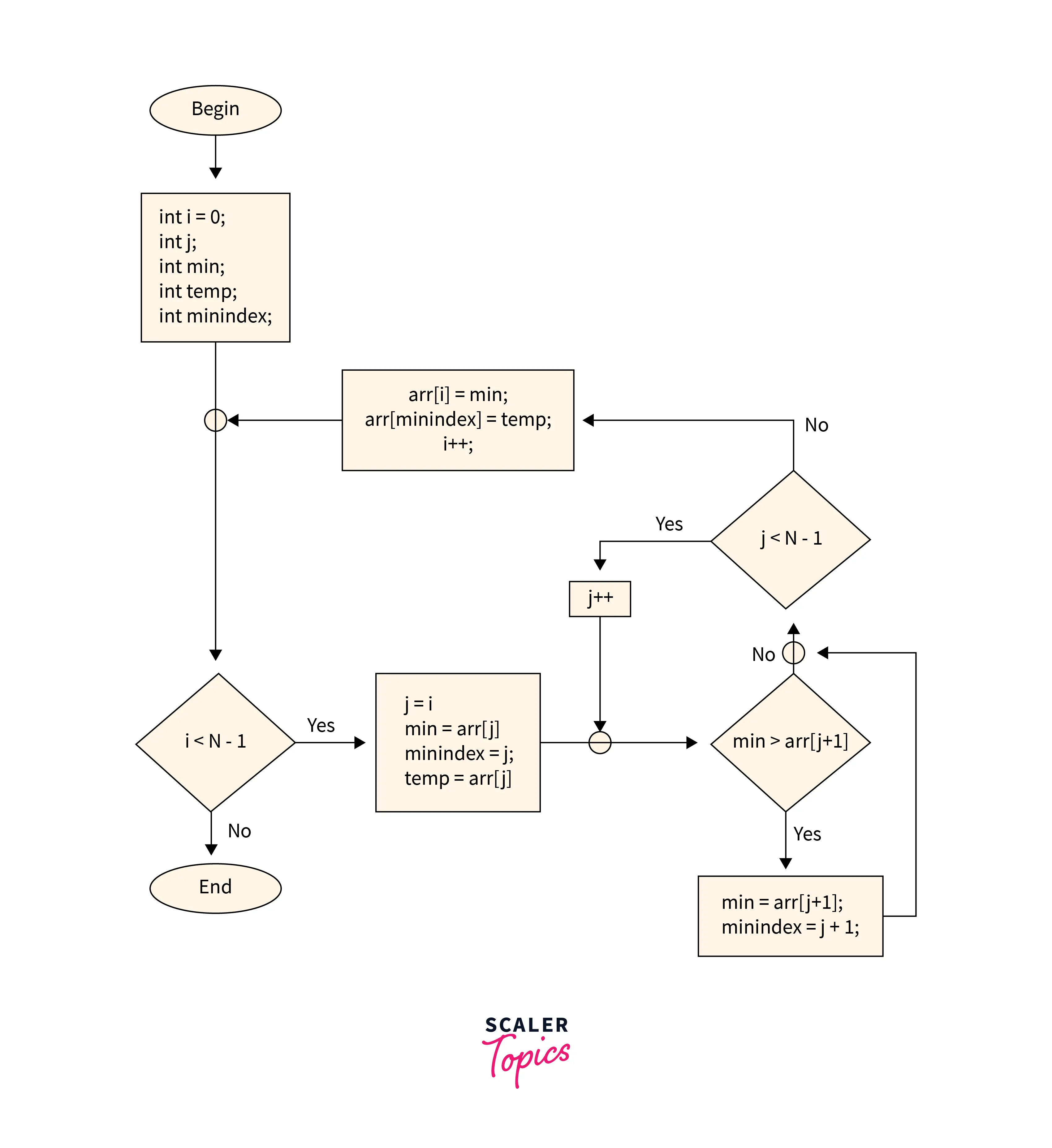
Now, let's look at the flowchart of working of selection sort C++.
Flowchart
In the following flowchart, we can see the program flow of the Selection sort algorithm in C++ and how the above-mentioned steps are implemented in the actual program.
Algorithm
Now, let's discuss the actual algorithm of the selection sort C++:
Implementation of Selection Sort
After going through the algorithm of the selection sort in C++, let's now look at the implementation of the selection sort in C++.
Let's take a look at an example:
Code:
Output
Explanation In the above program, we have initialized an array array with its elements. After that, we initialized a variable named size that shows the size of the given array. We have called the selectionSort() function from the main function, which will sort the array passed as an argument.
In the selectionSort() function, we have two for loops in which one is responsible for the selection of elements (Outer loop) and the other one is responsible for the comparison(Inner loop). Inside the outer for loop, we have initialized a variable indexMin, which initially considers the first index as a minimum. If any element is found smaller than the current minimum, then the indexMin variable is updated. When the smallest element of the array is found, we swap the first element's position with the minimum element's position. This swapping will continue until every element of the array gets placed at its correct position. At last, we printed the sorted array using a for loop.
Complexity Analysis of Selection Sort
Now, let's discuss the efficiency of the selection sort algorithm, which is done by analyzing the algorithm's complexity: Time (Worst, Average, and Best) and Space complexity.
Time Complexity
The Time Complexity of the Selection sort algorithm comes out to be O(n^2) according to the number of comparisons it takes to sort an entire array.
There are two loops involved in the algorithm. One loop selects elements inside the array one by one, which takes O(n) time. The other loop compares the selected element with other array elements, taking O(n) time. Therefore, the overall time complexity of the algorithm comes out to be O(n^2).
Let's discuss the algorithm's best, worst, and average time complexity.
Best Case Complexity
The best case occurs in selection sort when the given array or list is already sorted. But even after being a sorted array still, we have to make the same number of comparisons, and therefore, the best-case time complexity also comes out to be O(n^2).
Worst Case Complexity
The worst case occurs in selection sort when the given array is in descending order, and we have to arrange its elements in ascending order. Again, according to the comparisons, the worst-case time complexity also comes out to be O(n^2).
Average Case Complexity
The average case occurs when the array or list elements are randomly arranged rather than in ascending or descending order. Hence, the average case time complexity is** O(n^2)**.
The Time complexities of selection sort c++ are the same for every case possible, that is **O(n^2)**because we have to find the minimum element and place it at the correct place every time. We must traverse the entire array in the above cases to find that minimum element.
The Time complexity of the selection sort algorithm is O(n^2), which makes it inefficient for large data sets. Instead, it can be used for sorting small arrays or lists.
Space Complexity
The Space Complexity of the selection sort algorithm comes out to be O(1), which is Constant Space, as there is no extra space or data structure used in the algorithm other than the temporary variables used for swapping values of the array.
Characteristics of Selection Sort
Let's discuss some of the characteristics of selection sort C++:
- The selection sort algorithm is used when the size of an array is small, the cost of swapping elements does not matter, and the checking of each element inside the array is compulsory.
- In the selection sort, the time complexity is the same regardless of different cases and arrangements.
- In selection sort, the number of overall swapping or operations is less. Therefore, using it when swap operations are memory-consuming in the system is advisable.
Is Selection Sort Algorithm Stable?
No, selection sort is not stable as it works by finding the minimum element from the array and placing it at its correct position with the help of swapping with the element at the position of that minimum element.
Is Selection Sort Algorithm in Place?
Yes, the selection sort algorithm is in place because we don't need extra space to implement it on any list or array.
Conclusion
- Selection sort is an in-place comparison sorting algorithm that rearranges elements in rounds or iterations.
- If we have n elements inside an array, the array takes (n-1) iterations or rounds to fully sort.
- The Time Complexity of the Selection sort algorithm is O(n^2) according to the number of comparisons it takes to sort an entire array.
- The Space Complexity of the selection sort algorithm comes out to be O(1), which is Constant Space as no extra space or data structure is used.
- The Time complexities of selection sort c++ is the same for every case possible (Best case, Average case, and Worst case) is O(n^2) because we have to find the minimum element and place it at the correct place every time.
- The selection sort algorithm is used when the size of an array is small, the cost of swapping elements does not matter, and the checking of each element inside the array is compulsory.
- Selection sort is not a stable algorithm compared to other sorting algorithms.
