Priority Queue in C++
Learn via video course

Overview
Priority Queue is a standard template library (STL) container in C++, in which the top element is either the largest or the smallest of all the elements(depending on the type of the priority queue). However, the highest element is always the default in the C++ STL.
Generally, The time complexity of operations like insertion and deletion in the priority queue in C++ is .
Scope
- In this article, we will learn what a priority queue is, when, and how to use it.
- We will learn the internal working of the priority queue and different operations.
- Also, We will learn about different STL functions that can be used in the priority queue with examples.
Introduction
We are familiar with queues as one of the fundamental data structures taught in our classes. A priority queue is a special type of queue. A queue works on the principle of FIFO; A Priority Queue in C++ works on the principle of giving priority to the max(or min) element.
Basic Syntax
The general syntax of Priority Queue in C++ is:
Let us understand this with code:
In the above code, we have created a Priority Queue in C++ where we insert three elements, i.e., 5, 15, and 10. After inserting the elements, we display all the elements of a priority queue by using a while loop.
Output:
Operations of Priority Queue in C++
The basic operations of a priority queue are inserting, removing, and peeking elements.
1. Inserting an Element into the Priority Queue
The steps below add an element to a priority queue (max-heap).
- At the bottom of the tree, add the new element.
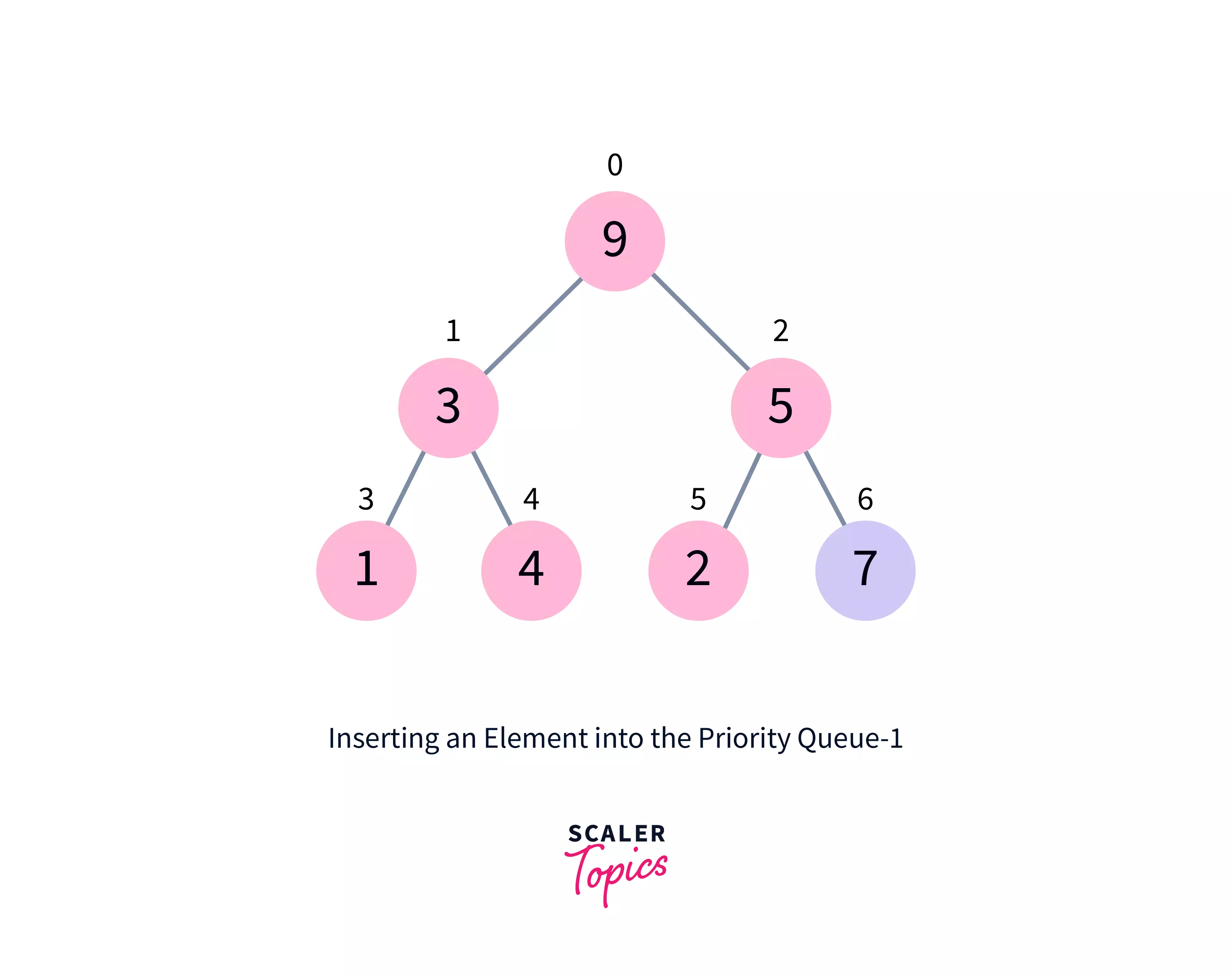
-
Heapify the tree.
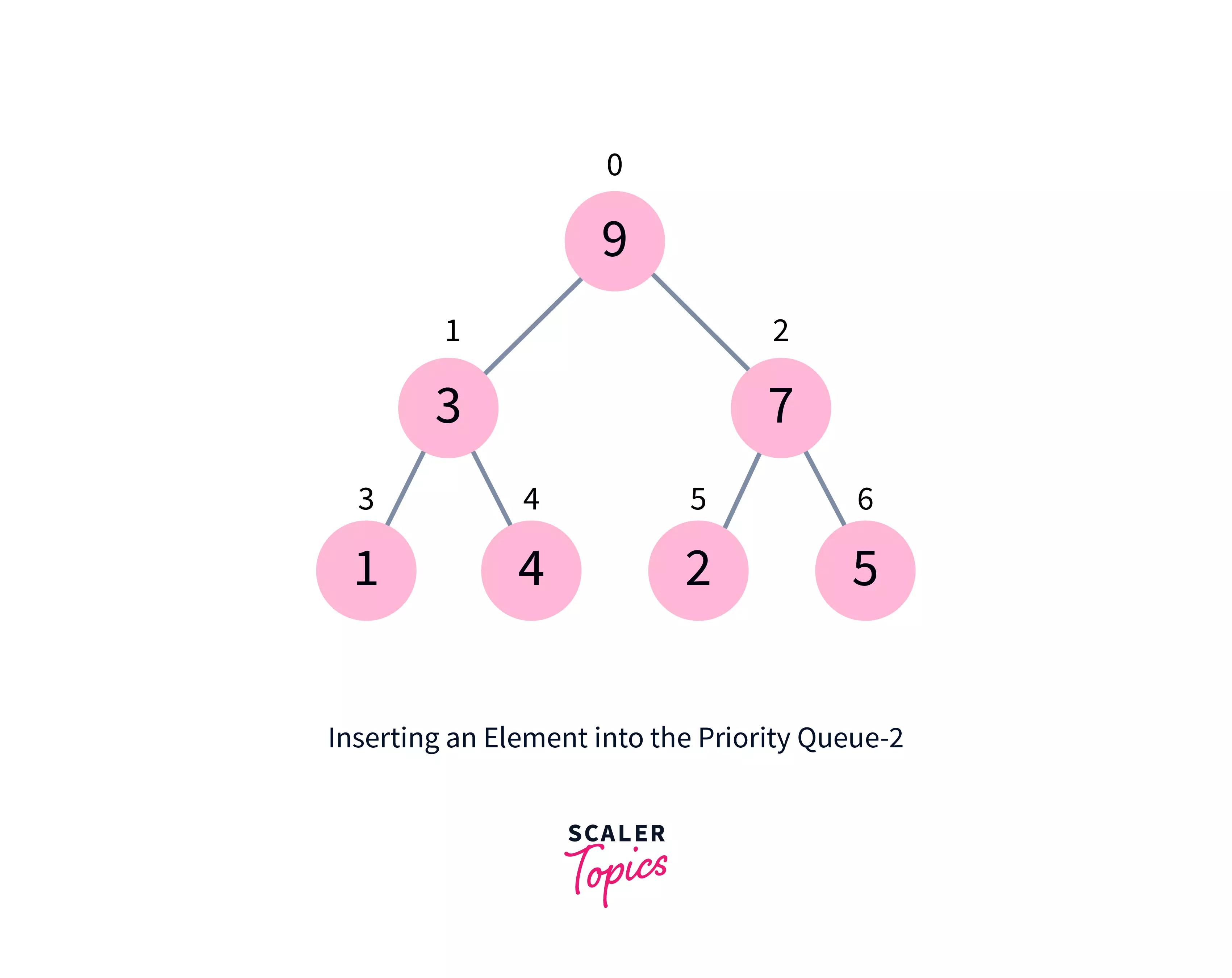
-
An algorithm for adding a new element to a priority queue (max-heap)
-
For Min Heap, the above algorithm is modified so that parentNode is always smaller than newNode.
-
Generally, The time complexity of insertion in the priority queue in C++ is .
2. Deleting an Element from the Priority Queue
The following is how to remove an entry from a priority queue (max-heap):
- Choose the element to be removed.
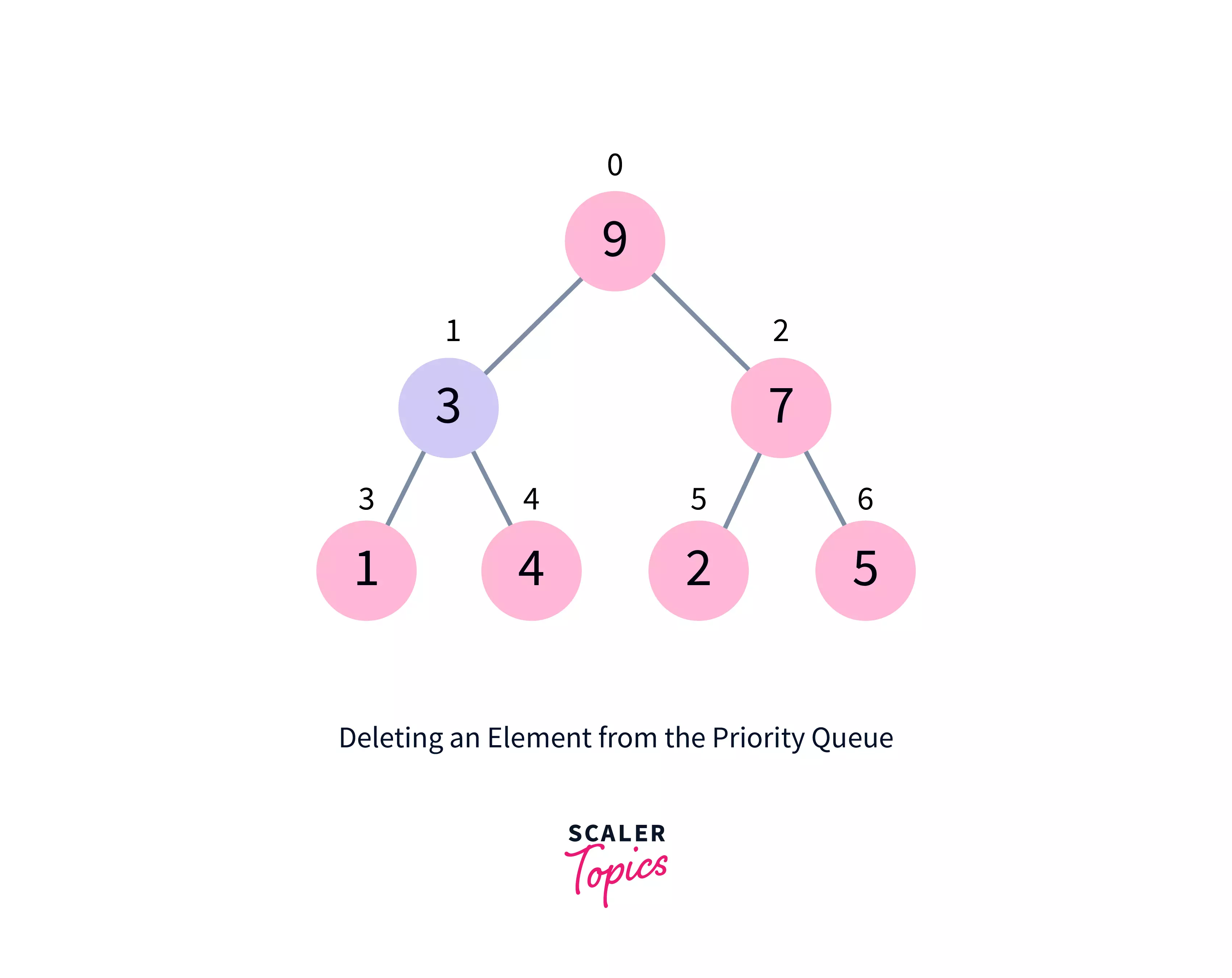
- Replace it with the last element.
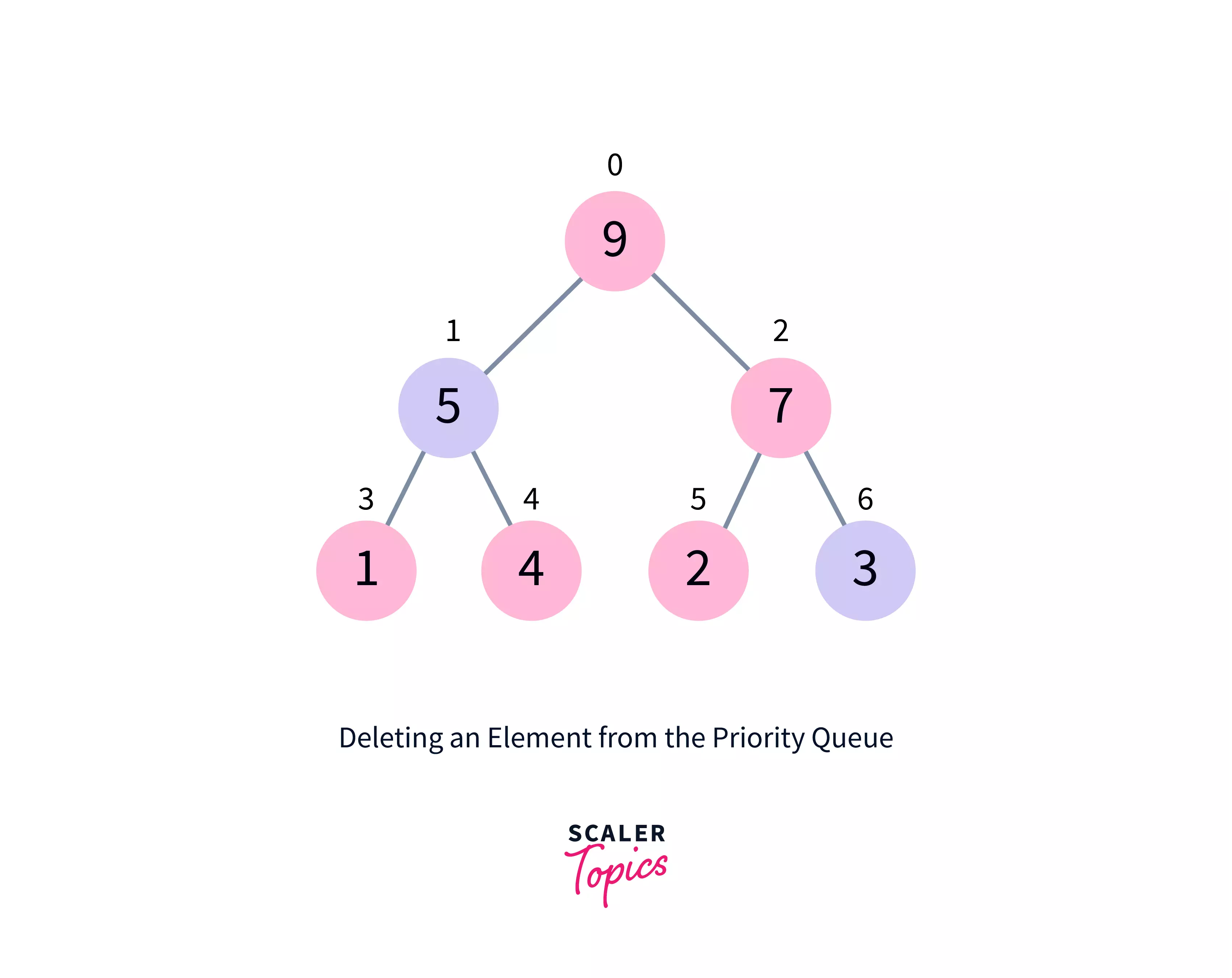
- Remove the final element.
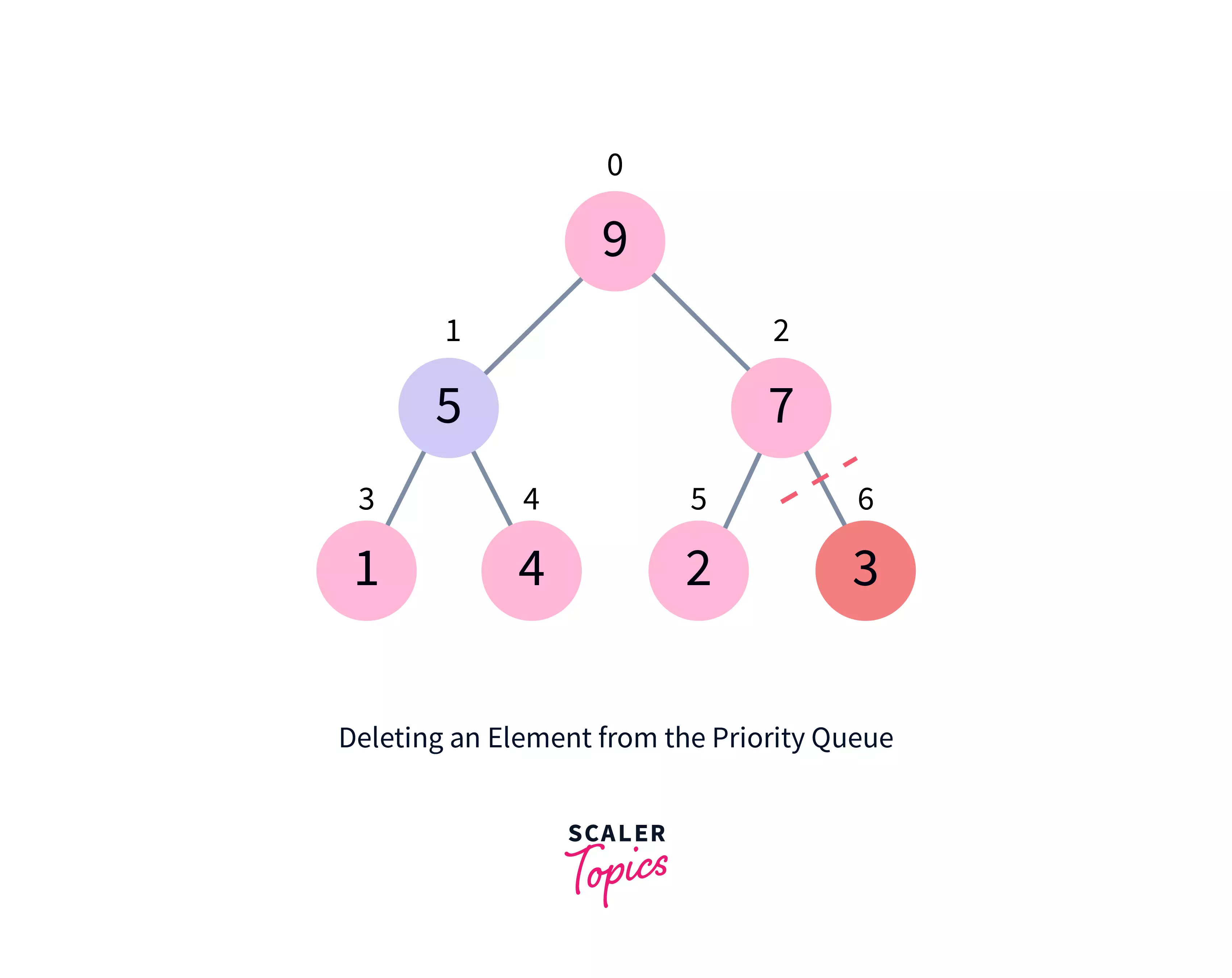
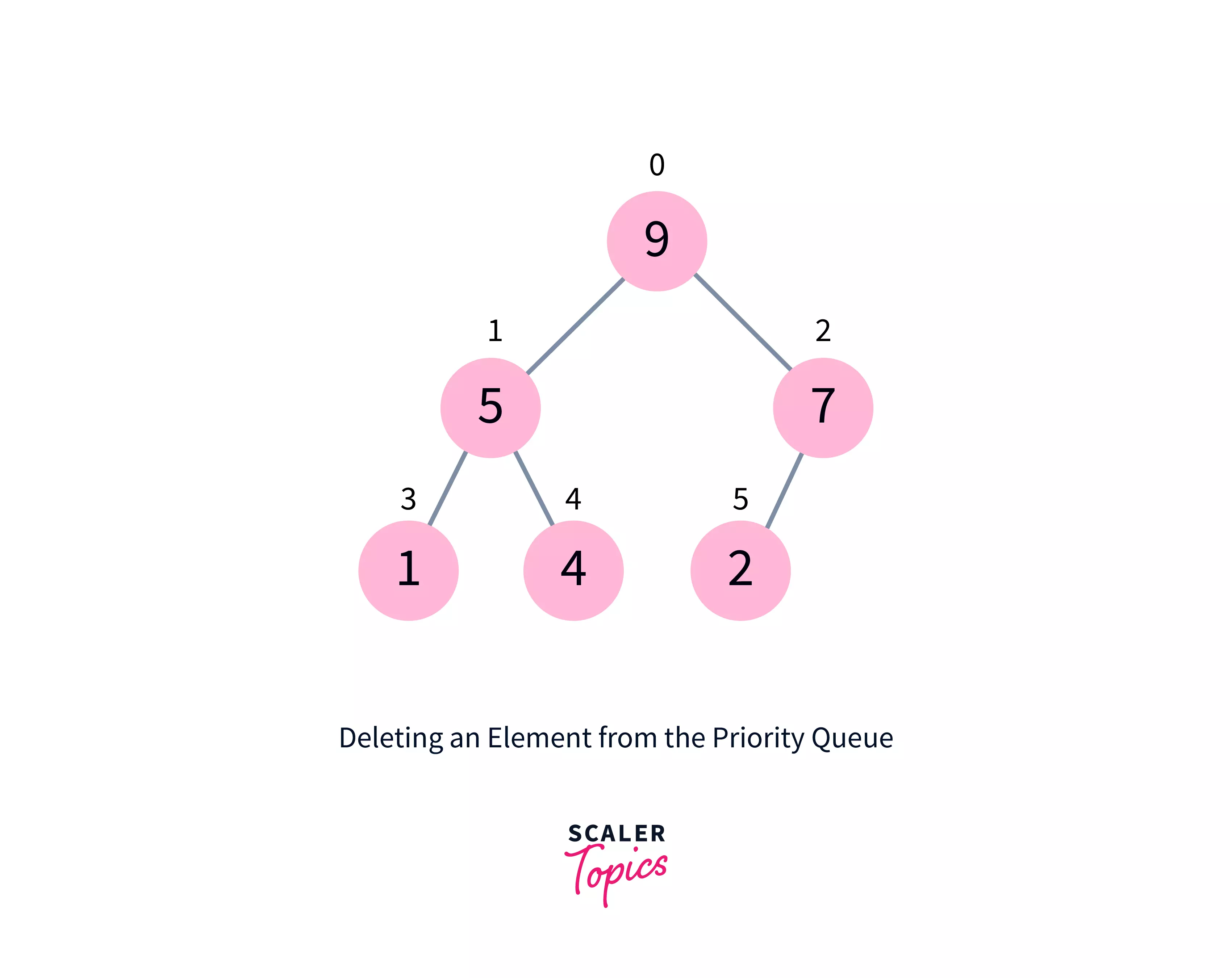
- The tree should be heapified.
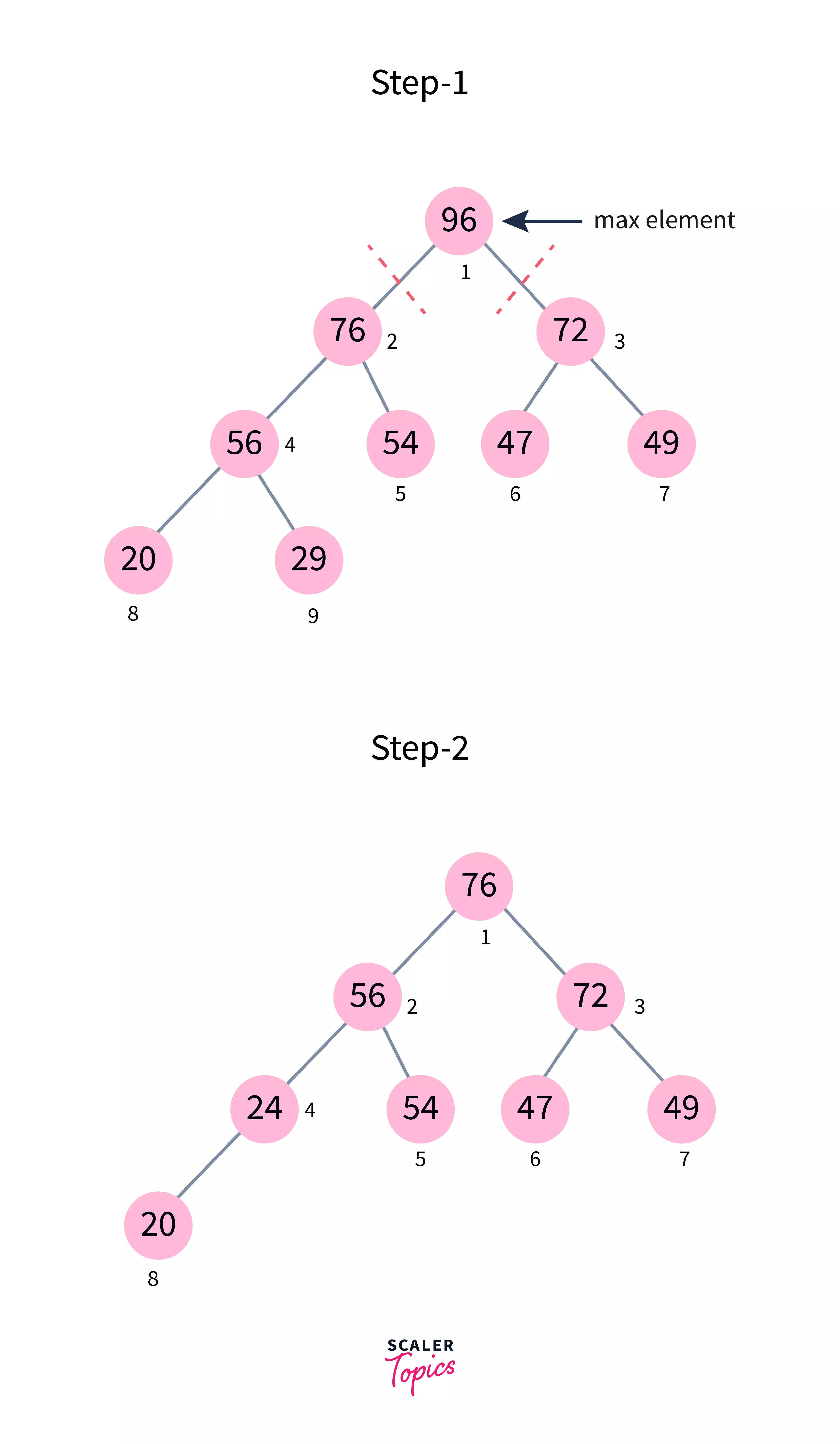
- Algorithm for deletion of an element in the priority queue (max-heap)
- For Min Heap, the above algorithm is modified so that both childNodes are smaller than currentNode.
- Generally, The time complexity of deletion in the priority queue in C++ is .
3. Peeking from the Priority Queue (Find max/min)
Without removing the node, the Peek operation returns the maximum element from Max Heap or the minimum element from Min Heap.
For both the maximum heap and the minimum heap
Generally, The time complexity of peek in the priority queue in C++ is .
4. Extract-Max/Min from the Priority Queue
Following the removal of a node from a Max Heap, Extract-Max returns the node with the highest value, whereas Extract-Min returns the node with the lowest value.
Priority Queue STL Functions
| Method | Definition |
|---|---|
| empty() | Returns whether the queue is empty. |
| size() | Returns the size of the queue. |
| top() | Returns a reference to the topmost element of the queue. |
| push() | Adds the element ‘g’ at the end of the queue. |
| pop() | Deletes the first element of the queue. |
| swap() | Used to swap the contents of two queues if they are of the same kind; however, their sizes may vary. |
| emplace() | Used to insert a new element into the priority queue container. |
Example Explaining all Important Priority Queue Functions
Inserting Elements in a Priority Queue:
Output
Accessing elements in a Priority Queue:
Output:
Deleting Elements in a Priority Queue
Output:
Program demonstrating every STL Method of a Priority Queue
Output:
Difference Between Priority Queue and Queue
| Priority Queue | queue |
|---|---|
| Priority Queue Works on the principle of the highest priority element will be deleted first | Queue Works on the principle of FIFO(First In First Out) |
| The queue is a data structure with a front and back where insertion takes place from the back and removal takes place from the front | A Priority queue does not have specified ends, so insertion doesn’t happen at a specific end. Deletion also does not happen at a specific end. |
Applications
-
Priority queue for Dijkstra's Shortest Path Method: While the graph is represented as an adjacency list or matrix, the priority queue may be utilized to extract the minimum efficiently when implementing Dijkstra's algorithm.
-
Prim's algorithm: It's used to build Prim's Algorithm, which stores node keys and extracts the smallest key node at each step.
-
Data compression: It is used in Huffman codes to compress data.
-
Artificial Intelligence: A Search Algorithm*: The A* search algorithm searches for the shortest path between two vertices in a weighted network, prioritizing the most promising paths. The priority queue (also known as the fringe) keeps track of undiscovered routes, with the one with the shortest lower bound on the overall path length receiving the most attention.
-
Heap Sort: Heap sort is commonly accomplished using Heap, a Priority Queue implementation.
-
System software: It's also used in operating systems for load balancing (server-side load balancing) and interrupt management.
Conclusion
- We learned about the basics of the priority queue in C++, like definition, operations, and functions.
- We also learned about the implementation of Priority Queue in C++ and its real-life use cases of Priority Queue.
- We also did a comparative study on Priority Queue and Queue.
