Combinatorics

Overview

Combinatorics is the area of mathematics that is concerned with counting as well as understanding the different arrangements of objects of a set under given constraints. Combinatorics in itself is a pretty large domain and is often used in solving problems of other domains too, such as topology, probability theory, etc.

Scope of Article

This article is meant to be an introduction to basic combinatorics. Thus, we will be discussing some basic rules of combinatorics, namely the sum and product rules of combinatorics, followed by a discussion on permutation v/s combinations of objects.

In the later half, we also discuss the Pascal's Triangle, alongwith some useful combinatorial identities. Towards the end we see some applications of combinatorics.

Takeaways

Combinatorics techniques are needed to count, enumerate, or represent possible solutions in the process of solving application problems.

What Is Combinatorics?

Suppose you're watching the IPL. 8 teams are going to play this season. There are no sub-groups, and all groups are meant to play with each other at least once before the quarter-finals.

Since you are planning to watch this entire season with your flat-mates, you all want to pre-plan the budget for pre-quarterfinal matches (all matches starting from quarter-finals will be watched at another friend's house who possesses a bigger screen television).

Now you want to know how many such matches will be played by the teams. Luckily, you remember the concept of combinations that you learnt in the 11th standard in school. Therefore, you understand that this problem reduces to finding the number of ways you can choose two teams from the set of eight teams. The final answer will be obtained by multiplying the last result by 2 since all teams will play with each other twice.

Therefore, the final answer will be

2\times{{}^{8}C_{2}} = 2\times \frac{8!}{2!\times6!} = 56

This small example shows how the concepts of combinatorics can be used in the daily life of any person. More such problems can be found in poker games, wedding arrangements, etc.

But what exactly is combinatorics?

Combinatorics is the branch of mathematics that concerns itself with counting. This counting often refers to the study of arrangements of objects of a given set under some defined constraints, but that is not all. The number and variety of topics that are generally studied under the umbrella of combinatorics is so large, there is no strict definition of what exactly a combinatorial problem is.

Most generally, the combinatorial problems deal with:

enumeration (counting)
proving (or disproving) the existence
construction
optimization

of given structure(s) within given constraints/properties.

Note: Structures are nothing but sets with some defined properties.

For example, the set of integers belong to the algebraic structure ring, in which rules like associativity of addition and multiplication, the existence of additive inverse, etc. hold true.

The exact meaning of a structure would depend on the context.

The reader should not worry themselves with such rigorous definitions, since this is an introductory article. We will be discussing the enumeration or the counting part of combinatorics in this article. Exploring further literature on various domains of combinatorics is up to the interest of the reader.

Basic Rules of Combinatorics

There are some basic rules/principles which are very frequently used while solving combinatorial problems. These principles are:

Addition Principle (sum rule)
Multiplication Principle (product rule)

These rules/ principles are often used together in conjunction with one another. We will see all of them with appropriate examples which will help you understand the rules much better.

Sum Rule

The sum rule can be stated as follows:

If one task A can be accomplished in $a$ ways and another completely separate task B can be accomplished in $b$ ways, then we can accomplish either of those tasks in $a+b$ ways.

Let us understand this with the help of an example.

Example 1: Suppose you want to buy a chocolate bar. The shopkeeper asks you whether you want to buy a Nestle chocolate or a Cadbury chocolate. You want to see the choices that the shop has to offer, so you look at the shelf. You find there are 5 different Nestle chocolates and 7different Cadbury chocolates.

Solution: Choosing any chocolate can be broken down into two mutually exclusive and exhaustive sub-tasks; choosing a chocolate from the Nestle shelf or choosing a chocolate from the Cadbury shelf.

Task A: Choosing a bar of chocolate from Nestle brand can be done in $a = 5$ ways

Task B: Choosing a bar of chocolate from the Cadbury shelf can be done in $b = 7$ ways.

Therefore, the task of choosing one chocolate from either of these shelves (equivalent to performing either task A or B) can be done in

a + b = 5 + 7 = 12 \ \text{ways}

In some texts, the sum rule is often described using the set notation in the following manner.

If we have pairwise disjoint partitions $S_1, S_2, S_3....,S_n$ of a set S, the cardinality of the set S can be found out using the cardinalities of the given partitions. That is

\big|S\big| = \big|S_1\big|+\big|S_2\big|+\big|S_3\big|...+\big|S_n\big|

This is just a generalized form of the sum rule we defined above. In any counting problem, we break down the objective task into mutually exclusive (that is pairwise disjoint) and exhaustive possibilities for the ways the given task/problem can be solved. Then we individually count the ways of these sub-tasks, and finally, add them to get our final answers.

To understand it, let us make a few changes to the example we used above.

Example 2: Suppose instead of just two brands, there were five such brands available for you to choose from. The brands and the kinds of chocolates available in them are as follows:

Nestle : 3 chocolates
Cadbury: 5 chocolates
Ferrero Group: 4 chocolates
Hershey: 5 chocolates
Amul: 4 chocolates

Now, in how many ways can you buy 1 chocolate?

Solution: The goal of buying a chocolate can be accomplished by completing exactly one of the following 5 tasks:

Task 1: Choosing a bar of chocolate from Nestle brand, can be done in $s_1 = 3$ ways. Task 2: Choosing a bar of chocolate from the Cadbury brand, can be done in $s_2 = 5$ ways. Task 3: Choosing a bar of chocolate from the Ferrero brand, can be done in $s_3 = 4$ ways. Task 4: Choosing a bar of chocolate from Hershey brand, can be done in $s_4 = 5$ ways. Task 5: Choosing a bar of chocolate from the Amul brand, can be done in $s_5 = 4$ ways.

That is, you could either only complete task 1, or only complete task 2, or task 3, and so on.

Using the sum rule, we say that our goal can be accomplished in

s_1+s_2+s_3+s_4+s_5 = 3+5+4+5+4 = 21 \text{ ways}

Product Rule

The product rule can be stated as:

If one task A can be accomplished in $a$ ways and another completely independent task B can be accomplished in $b$ ways, then we can accomplish both of those tasks in $a\times b$ ways.

This statement can be further generalized for n tasks as follows:

If you're given a list of pairwise independent tasks $(T_1, T_2, \cdots T_n)$ , and the $i^{th}$ task can be done in $a_i$ ways, then the number of ways of accomplishing all the given tasks will be

a_1 \times a_2 \times a_3...a_n

Notice the difference between the product rule and the sum rule. The sum rule counts the number of ways of doing exactly one task from a given list of tasks. Meanwhile, the product rule counts the number of ways of doing all the tasks. We will understand this better with the same example we used above, but with a slight change.

Example 3: Suppose you're at that shop, and suddenly four of your siblings call you and they demand a bar of chocolate each. But since each of your siblings have their own unique favourite brand of chocolates, you have to buy the chocolates from each of the five available options (Nestle, Cadbury, Ferrero, Hershey, and Amul). In how many ways can you do it?

The number of varieties of chocolates given under each brand is the same as the previous example.

Solution: The solution is pretty straightforward. You have to choose one chocolate from Cadbury, and one chocolate from Nestle, and one chocolate from Ferrero, and one chocolate from Hershey, and one chocolate from Amul.

Therefore, according to the product rule, we can make $m$ combinations of 5 chocolates, where

m = s_1 \times s_2 \times s_3 \times s_4 \times s_5 = 3 \times 5 \times 4 \times 5 \times 4 = 1200

Please note how we have defined our solution. In the discussion of the example in the sum rule, we used the keyword or to separate the different solution classes, while in this solution, we used the keyword and since all of them must be performed together to accomplish our goal (that was to buy 5 chocolates of different brands).

:::

Combinations of Objects

Combination of objects refers to the selection of $k$ objects from a set of $n$ objects and is given by

{}^nC_k = \frac{n!}{k!\times (n-k)!} = \binom{n}{k}

where $n!$ (read as n factorial) is defined recursively as:

n! = \begin{cases} 1 & n = 0 \\ \ n\times (n-1)! & n\gt0 \end{cases}

The combination of objects merely performs a selection, that is, the exact arrangement of the object chosen is not important here. Also, all the $n$ objects must be distinct to apply this formula.

Example: Suppose you went to an ice-cream parlor, and since you were their 100th customer today, you will get one different ice-cream free along with the one you order, therefore 2 ice-creams in total. In how many ways can you choose 2 ice-creams? There are 7 flavors on the menu today.

Solution:

Choosing any 2 ice-creams from the given 7 can be termed as a combination problem. Since the order doesn't matter here, we can safely use the formula we described above. Therefore, the number of ways we can choose ice-creams is:

{}^7C_2 = \frac{7!}{5!\times2!} = \frac{1\times 2\times 3\times 4\times 5\times 6\times 7}{(1\times 2\times 3\times 4\times 5)\times (1\times 2)} = \frac{42}{2} = 21

Therefore, we can make 21 pairs of ice-creams.

Combination With Repetitions

Imagine that in the previous example, if we were allowed to choose one particular ice cream more than once. Then, would the answer still be valid? No.

Why?

Because the combination formula described above is used to choose $k$ distinct objects from a set of $n$ distinct objects (without any ordering of course). But what if we want to select some particular $i^{th}$ object more than once? Then we will use the result described below.

If you're given a set of N distinct objects, and each object has an infinite supply. Therefore, you can choose any item of this given set any number of times you want. Now, in such a situation, if you want to choose/collect $k$ (not necessarily distinct objects), the number of ways you can do it is:

{}^{n+k-1}C_k = \frac{(n+k-1)!}{k!\times (n-1)!}

Let's two examples to understand the kind of situations where this result would be used.

Example: You've recently discovered a cave where there are 4 boxes filled with an infinite number of gems: one kind of gem in one box. The gems are diamonds, rubies, emeralds, and blue sapphires. You want to make a gauntlet of precious stones like the one Thanos had, but with these 4 kinds of stones. You've 6 slots in your gauntlets. In how many ways can you decorate your gauntlet? Note that you can use one stone more than once in your gauntlet.

Solution: Since repetitions are allowed, and the order of stones does not matter to us (for the sake of discussion), we will use the result we stated above.

Here: $n$ = Number of kind of stones = $4$
$k$ = Number of stones to choose = $6$

Therefore, the number of ways to decorate our gauntlet would be:

{}^{n+k-1}C_k = {}^{4+6-1}C_6 = \frac{9!}{6!\times 3!} = 84

Hence, we can make our gauntlet in 84 ways.

Note: Here, $k>n$ . Therefore, the formula for the combination without repetition $({}^nC_k)$ would not have been valid.

Example: You're given a set of 4 elements, that is, $\{a,b,c,d\}$ . From this set, you can choose any element at most 5 times. In how many ways can you form unordered triplets? Please note that the order of the elements of triplets won't matter here. Some examples of valid triplets are $abc, bbc, ccd, cdd,$ etc.

Solution: Since again we have to choose multiple copies of items that are identical in nature, we have to use the result we mentioned above. Here

$k = 3$
$n = 4$

So, the answer to the proposed problem would be:

{}^{n+k-1}C_k = {}^{4+3-1}C_3 = \frac{6!}{3!\times 3!} = 20

Interestingly enough, suppose if all the letters had been non-identical, that is, the set would have been like $\{a_1,a_2,..a_5, b_1...b_5, c_1...c_5, d_1...d_5\}$ , then the answer to our problem would have been

{}^{n}C_k = {}^{20}C_3 = \frac{20!}{3!\times 17!} = 1140

Permutations

Permutation (of objects) refers to an arrangement (or relative order) of objects. For example,

ab

and

ba

are two different permutations of letters $a$ and $b$ . Similarly, for letters $a$ , $b$ , and $c$ , the possible permutations are

abc, acb, bac, bca, cab, \text{ and } cba

Many combinatorial problems consist of counting permutations of some (possibly identical) objects.

Important Results: Suppose if there are $n$ distinct items, then there are

$n!$ ways to arrange them in a line.
$(n-1)!$ ways to arrange them in a circle

Let us use this concept in a simple example:

Example: How many words can be formed using the vowels of the English alphabet, that is, { $a,e,i,o,u$ } using each letter exactly once. Please note that it is not necessary for the word formed to be a valid English word.

Solution: Since we have to use each letter exactly once, therefore, we can say that this problem reduces to counting the distinct permutations of the vowels.

Since there are five vowels, the number of words that can be formed is:

5! = 5\times4\times3\times2\times1 = 120

Thus, we can form 120 words using the letters a,e,i,o,u exactly once.

Permutation With Repetition

If you see carefully, the result we described above is for distinct objects. What if all the objects are not distinct? Then if we use the $n!$ formula, we will overcount. Let's see an example to understand this case.

What is the number of ways to arrange the letters $a, a, b$ ? Since $n = 3$ , one could say that using the previous formula, the answer would be $3!=6$ . But is it so? Let us see the possible arrangements for $a,a,b$ :

aab, aba, baa

Why does this happen? To understand that, first let us consider that both the $'a'$ are different, that is $a_1$ and $a_2$ . In that case, the possible permutations are:

a_1a_2b,\ a_1ba_2,\ ba_1a_2,\ a_2a_1b,\ a_2ba_1,\ ba_2a_1

But since $a_1$ and $a_2$ are same, the following permutations are equivalent:

$a_1a_2b$ = $a_2a_1b$
$a_1ba_2$ = $a_2ba_1$
$ba_1a_2$ = $ba_2a_1$

To prevent this overcounting, we perform a division operation. We state the following result without any proof.

If there are $n$ items, out of which some items are of identical type $a_1$ , some items are of type $a_2$ , and so on. Then, the number of unique arrangements of these $n$ items are:

\frac{n!}{a_1!\ a_2!\ a_3!...a_n!}

Let's use this result in our previous example. The $n=3$ items, in this case, are $a, a, b$ , where the two items $'a'$ are identical. Therefore, the unique number of arrangements in that case are:

\frac{3!}{2!\ 1!} = 3

This is the same as the count we got after listing out the arrangement explicitly. :::

Applications Of Combinatorics

Combinatorics cover a wide range of applications.

Enumerative Combinatorics is widely used in counting problems, such as analyzing sequences, tree constructions, etc.
Other combinatorial techniques are used to study areas such as: a. Partition Theory b. Graph Theory c. Design Theory d. Finite Geometry and many more.
Combinatorics is also used in the field of probability theory to understand the occurrences of structures of certain features.

Pascal Triangle

While discussing the topic of combinations, we described the following notation for choosing $k$ out of $n$ items, that was, ${}^nC_k$ . This $C$ is called the binomial coefficient.

A table of binomial coefficients as shown below is popularly known as Pascal's triangle (sometimes also called Pascal-Pingala Triangle, or Pingala's Meruparastara).

pascal triange

This triangle shows the first 6 rows of the triangle. But how is this triangle generated? The rules are as follows:

Every row starts with 1 and ends with 1
The other in-between elements are just the sum of elements present in right and left in the previous row.

The image below shows the flow of the calculation:

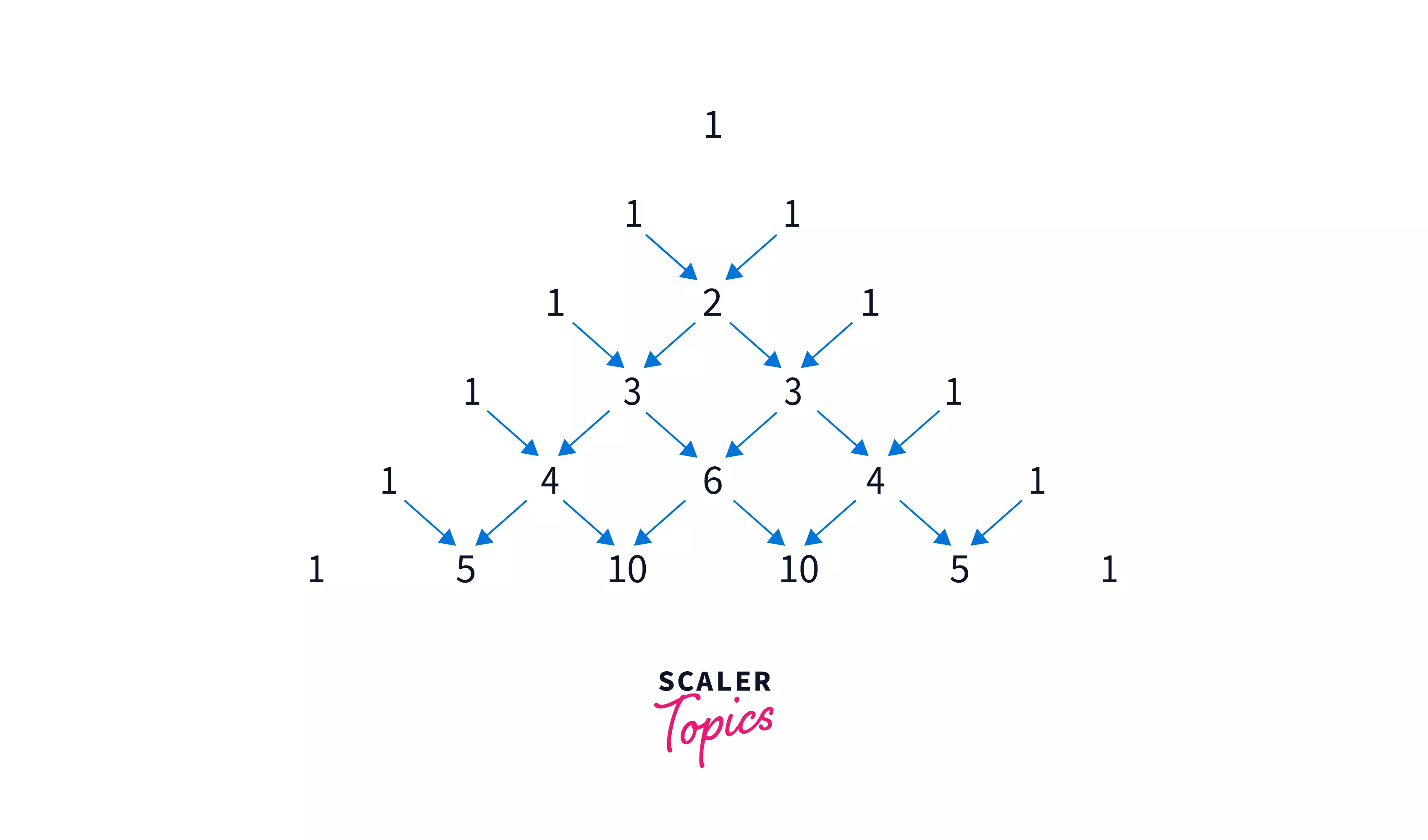
flow of calculation

But we still haven't seen how this relates to binomial coefficients. It's as follows:

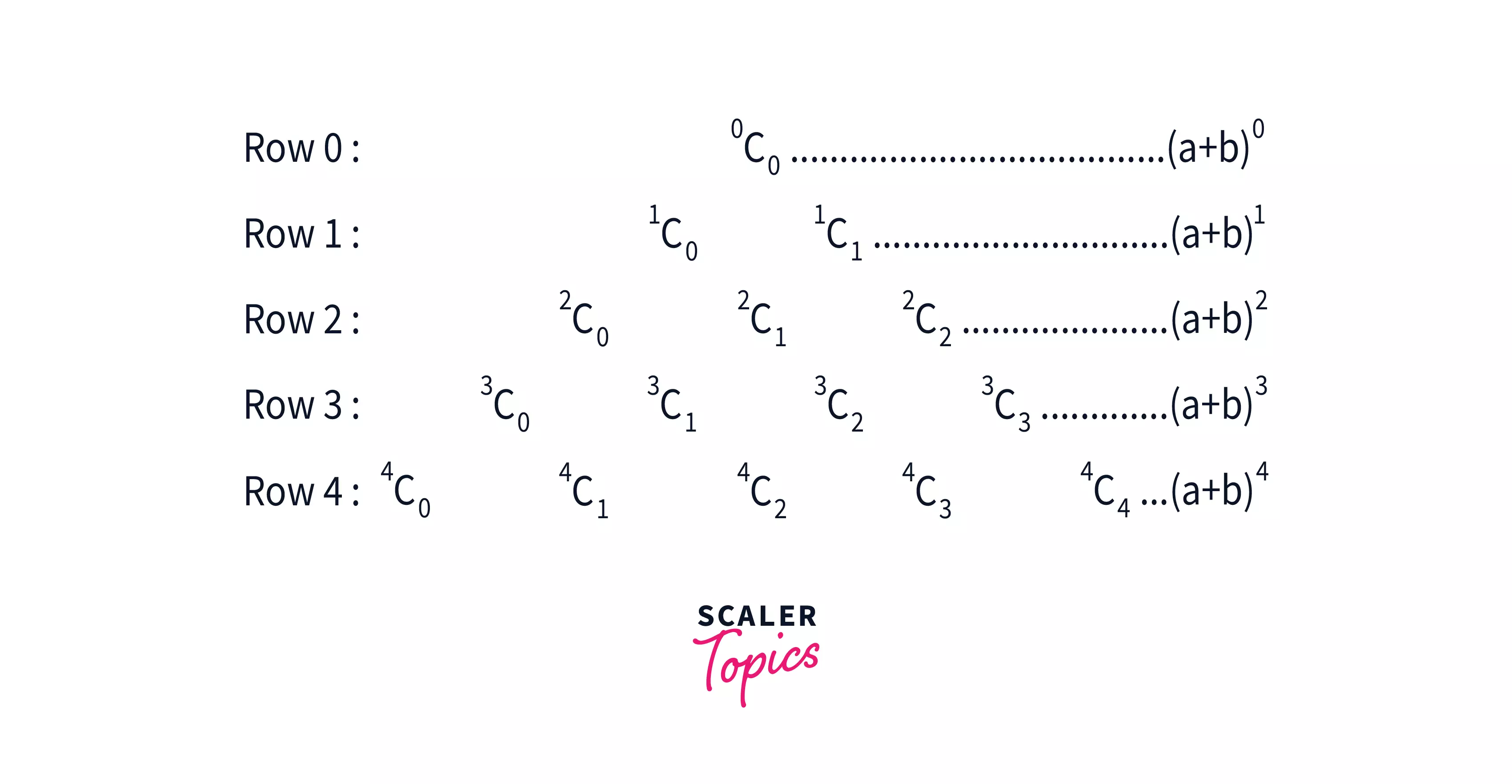
binomial coeffcient

As shown above, row $n$ provides us with the coefficients of binomial terms $a^ib^j$ upon expansion of $(a+b)^n$ , that is, ${}^nC_i$ .

For example, on expansion of $(a+b)^3$ , we get

a^3+3a^2b+3ab^2+b^3 = {{}^3C_0}a^3+{{}^3C_1}a^2b+{{}^3C_2}ab^2+{{}^3C_3}b^3

The coefficients are 1, 3, 3, 1, which are the same as the contents of row 3.

Interesting Properties of Binomial Coefficients

Below listed are some interesting properties of binomial coefficients, many of which could be verified using Pascal's triangle we showed above. 1.

\binom{n}{0} +\binom{n}{1}+\binom{n}{2}...\binom{n}{n} = 2^n

\binom{n}{0} +\binom{n}{2}+\binom{n}{4}... =\binom{n}{1} +\binom{n}{3}+\binom{n}{5}...= 2^{n-1}

1\cdot\binom{n}{1} +2\cdot\binom{n}{2} +3\cdot\binom{n}{3} +...n\cdot\binom{n}{n} = n\cdot2^{n-1}

\binom{n}{0}-\binom{n}{1}+\binom{n}{2}-\binom{n}{3}\dots(-1)^n\binom{n}{n} = 0

The following result is known as the Hockey Stick Identity:

\sum_{i=r}^{n}{\binom{i}{r}} = \binom{r}{r}+\binom{r+1}{r}+\binom{r+2}{r}...\binom{n}{r} = \binom{n+1}{r+1}

The following result is known as the reduction formula:

\binom{n}{r} = \frac{n}{r}\binom{n-1}{r-1}

Similarly, the following result is called increment formula:

\binom{n+1}{r+1} = \frac{n+1}{r+1}\binom{n}{r}

\binom{n}{r}+\binom{n}{r-1} = \binom{n+1}{r}

Conclusion

Combinatorics is a branch of mathematics that concerns itself with enumerating structures, proving (or disproving) their existence, constructing, and optimizing them.
Sum Rule (binary version): If one task A can be accomplished in $a$ ways and another completely separate task B can be accomplished in $b$ ways, then we can accomplish either of those tasks in $a+b$ ways. This can easily be extended to $n$ tasks.
Product Rule (binary version): If one task A can be accomplished in $a$ ways and another completely independent task B can be accomplished in $b$ ways, then we can accomplish both of those tasks in $a\times b$ ways. This can be also be extended to $n$ tasks.
$n!$ (read as n factorial) is defined a. recursively as:

$n! = \begin{cases} 1 & n = 0 \\ \ n\times (n-1)! & n\gt0 \end{cases}$

b. Iteratively as:

$n! = 1\times2\times3\cdots n$
Combination of objects refers to the selection of $k$ objects from a set of $n$ objects, and is given by

{}^nC_k = \frac{n!}{k!\times (n-k)!} = \binom{n}{k}

If some objects are present in amounts more than the count of total objects we have to select (that is $k$ ), then, the number of ways we can make the selection is:

{}^{n+k-1}C_k = \frac{(n+k-1)!}{k!\times (n-1)!}

Permutation (of objects) refers to an arrangement (or relative order) of objects. if there are $n$ distinct items, then there are: a. $n!$ ways to arrange them in a line. b. $(n-1)!$ ways to arrange them in a circle
If there are $n$ items, out of which some items are of identical type $a_1$ , some items are of type $a_2$ , and so on. Then, the number of unique arrangements of these $n$ items are:

\frac{n!}{a_1!\ a_2!\ a_3!...a_n!}

Pascal's triangle (sometimes also called Pascal-Pingala Triangle, or Pingala's Meruparastara) is a triangle of binomial coefficients. The $n^{th}$ row (numbering starts from $0$ ) gives the coefficients for $a^ib^j$ in expansion $(a+b)^n$ , that is, ${}^nC_i$ .
1. The following result is known as the Hockey Stick Identity:

\sum_{i=r}^{n}{\binom{i}{r}} = \binom{r}{r}+\binom{r+1}{r}+\binom{r+2}{r}...\binom{n}{r} = \binom{n+1}{r+1}

The following result is known as the reduction formula:

\binom{n}{r} = \frac{n}{r}\binom{n-1}{r-1}

Similarly, the following result is called increment formula

\binom{n+1}{r+1} = \frac{n+1}{r+1}\binom{n}{r}

Basics of Combinatorics

Learn via video course