Divide and Conquer Algorithm

Introduction to Divide and Conquer Algorithm

One of the most peculiar things, when it comes to problem-solving, is that a single problem might have a variety of algorithmic approaches to its solution. Owing to this fact, there exist thousands of known algorithms in the world of computer science as of now, with the possibility of new additions to this tally always on the table.

For the sake of understanding and studying these algorithms in a generalized, and hence efficient manner, computer scientists have over time developed some classes these algorithms can be grouped under.

One such paradigm in the world of algorithms is known as the “divide and conquer” algorithm. As the name itself signifies, the divide and conquer algorithmic approach involves breaking down a given problem into smaller sub-problems, post which these sub-problems are individually solved before being merged again into the output solution.

The logic behind this is that instead of performing a one-shot solution of a significant, particularly complex problem, it is generally easier to break down the problem into simpler, smaller problems which tend to be easier to solve.

While the above-given definition gives you a vague idea about what divide and conquer algorithms are, we aim to dive deeper into it and establish a thorough understanding of the subject using this article, where we are going to learn how the divide and conquer algorithms work.

Let us look at the same in the next section.

How Does the Divide and Conquer Algorithm Work?

As we read earlier, while following the divide and conquer algorithmic approach, one breaks down the given problem at hand into smaller sub-problems, which are then solved individually, before being merged back into the final solution.

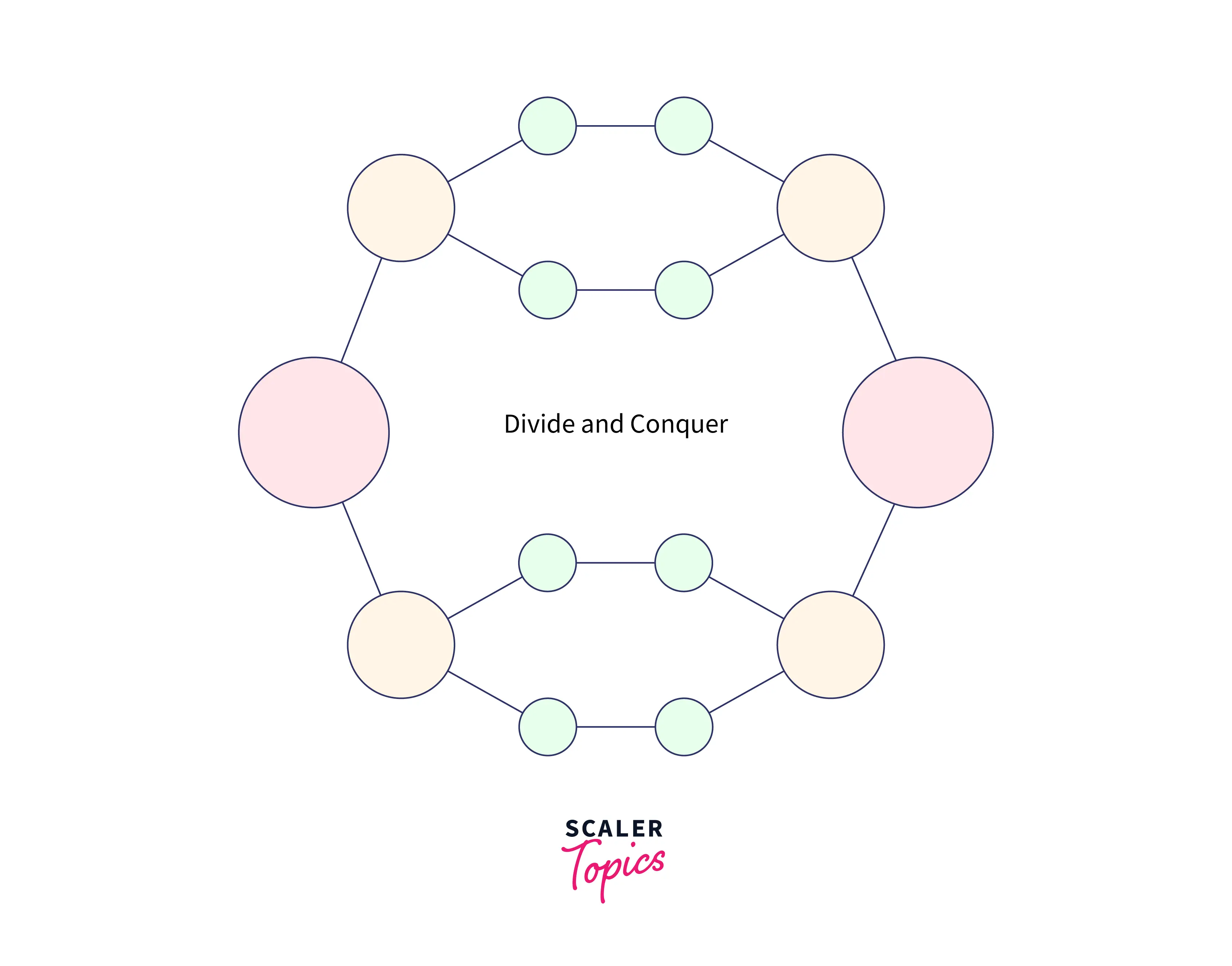
The divide and conquer algorithms work on the principle of atomicity. The notion here is that it is easier to study (and hence, solve) the smallest unit of a problem than the whole problem altogether. Following this principle, in the divide and conquer algorithm, we keep dividing the given problem into smaller problems to the point that these smaller sub-problems can no longer be further divided.

This stage is known as the atomic state of a problem. The algorithm then solves these “atoms” individually, and then finally, the solution of all the sub-problems is merged into the final output solution. The entire process can be illustrated with the help of the diagram given below :

Let us now take a look into each one of the individual stages of the divide and conquer algorithms, namely :

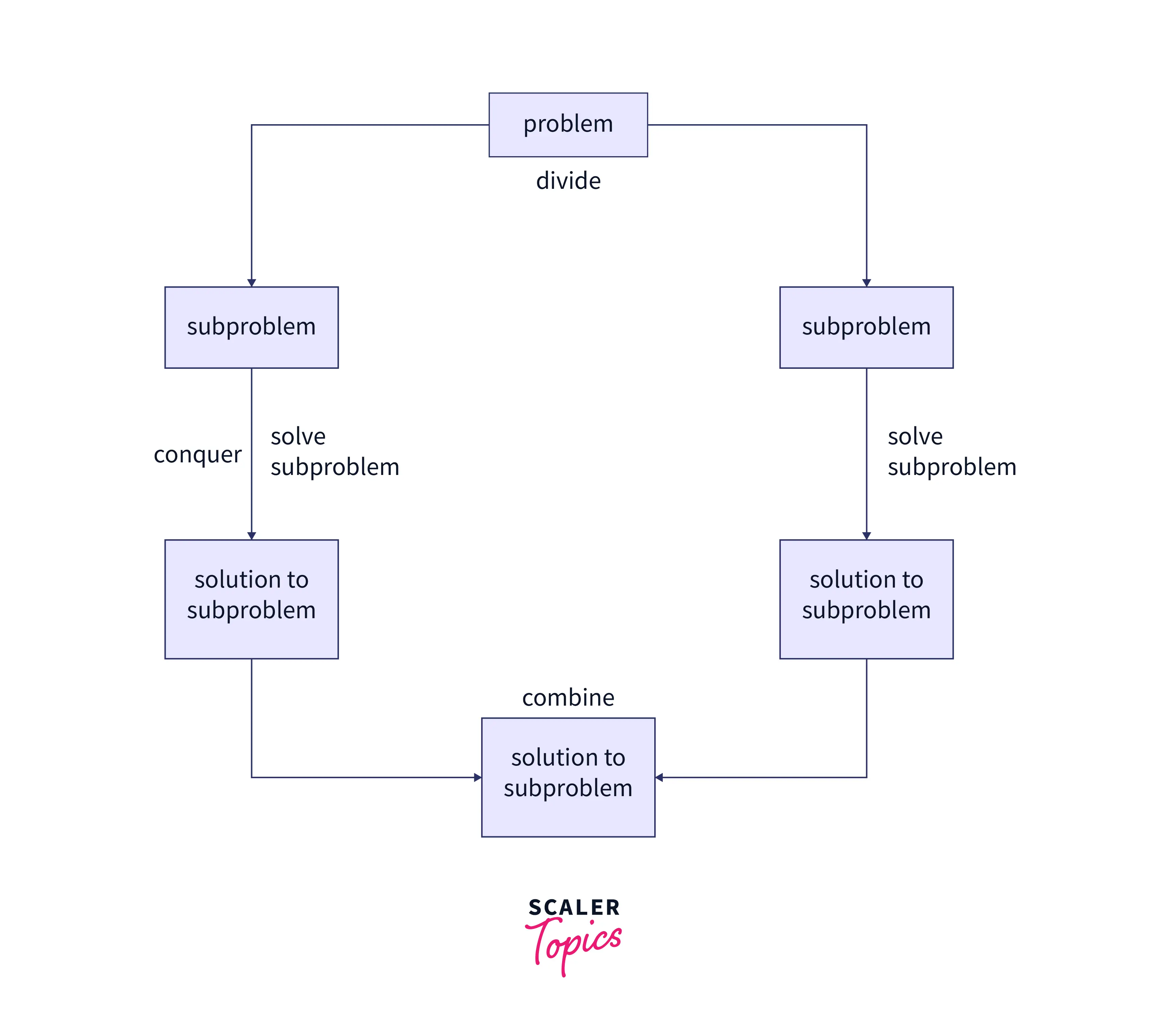
• Divide :
  This step constitutes dividing the problem at hand into smaller, atomic problems. An inherent rule here is that these atoms must be representative of the original problem, which simply implies that these sub-problems have to be a part of the original problem. The divide component of the divide and conquer algorithm follows a recursive approach for breaking down the problem until none of the sub-problems are further divisible. The output of the algorithm, after this step, are atoms of the original problem that can now be worked upon for deriving a solution.

• Conquer :
  This is the intermediary step within the divide and conquer problem-solving approach, where in theory, all the individual atomic sub-problems are solved and their solutions are obtained. However in practice, generally the original problem has already been broken down in the last stage (i.e., the dividing stage) to a level that the sub-problems are considered “solved” on their own.

• Merge :
  Merge constitutes the final stage of the divide and conquers algorithm, where the individual solutions obtained from the previous stage of the algorithm are recursively merged till the solution of the original problem is formulated. The output derived after this stage is the required solution for the problem.

As we can see from the description of the above-mentioned steps, recursion is at the core of the divide-and-conquer algorithms. Whether it is breaking down the original problem into sub-problems or merging the individual solutions into the final output, both tasks are done recursively. Thus, to establish a strong understanding of the divide and conquer approach, a good understanding of recursion is mandatory.

Now let us further strengthen our understanding of the algorithm with the help of an example. We will take a look at merge sort, which is a sorting algorithm based on the divide and conquer approach.

For example, we will be considering the following unsorted array of integers.

The output of the algorithm will be a sorted array with the values arranged in increasing order.

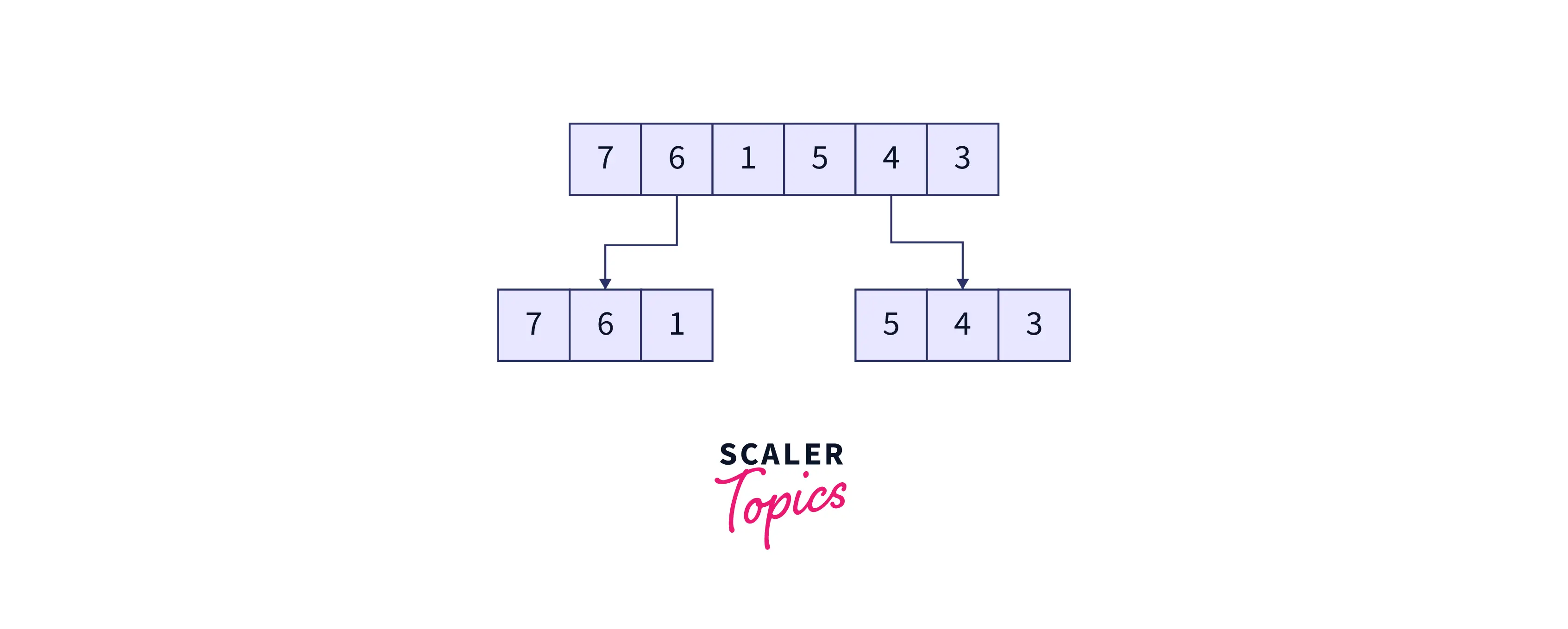
1. As we read earlier, the first step of the algorithm will be to divide the problem at hand into atomic sub-problems. In merge sort, we keep dividing the initial array (and thereafter the sub-arrays) into two halves recursively till the subarrays are no longer divisible, i.e., the size of the sub-arrays is one. This process can be visualized as follows :

   • Divide the original array into two parts.

   • Divide the two sub-arrays, and hence the subsequent sub-arrays further until the size of all the sub-arrays equals one.

   The resultant sub-arrays will be as follows.

2. Now, we enter the conquer step of the algorithm where, as per the definition, these sub-arrays will be sorted individually. However, in practice, an array of sizes does not need any sorting. So this step is complete by default.

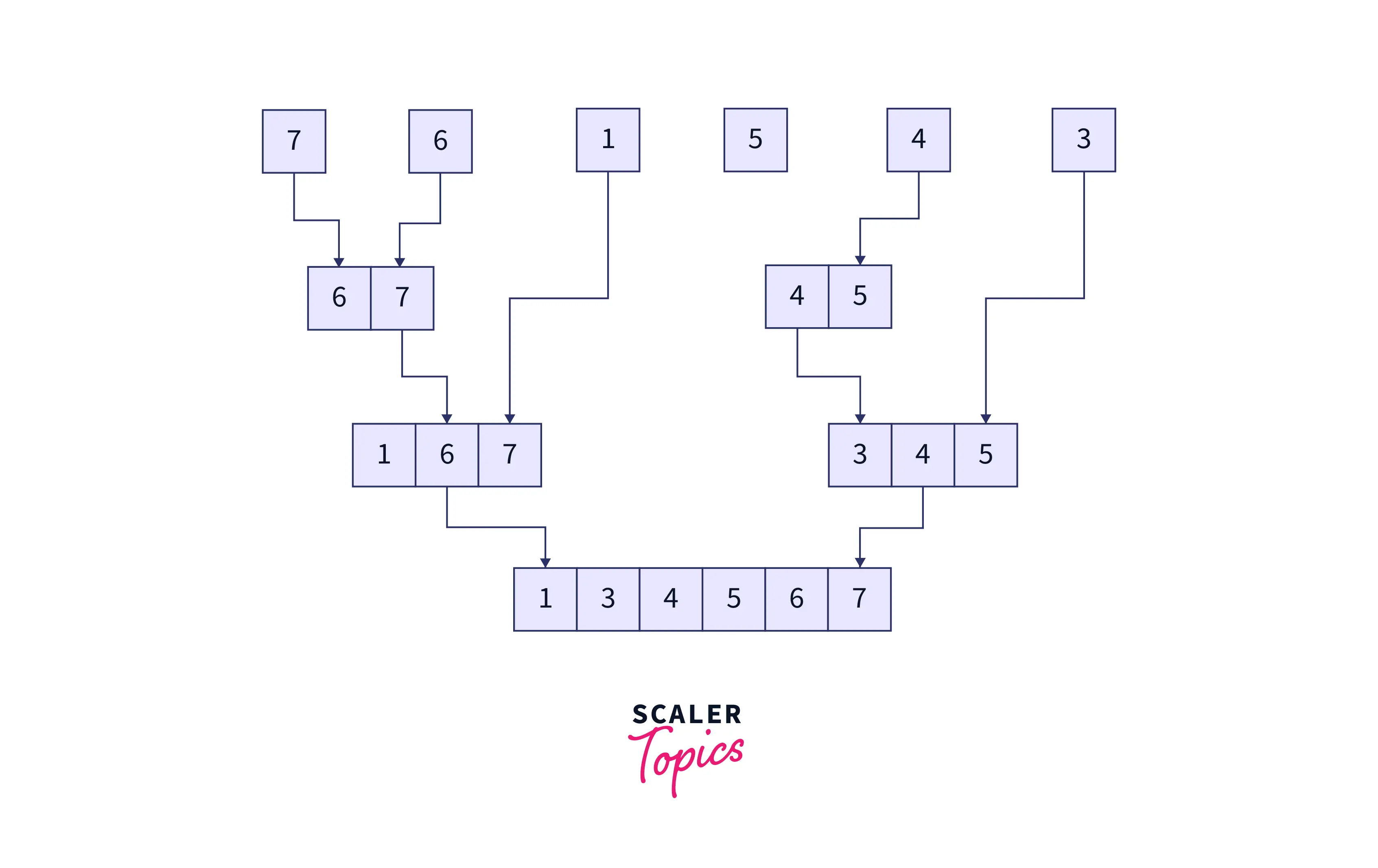
3. Finally, we arrive at the merge stage of the merge sort algorithm. Here, we will recursively combine the subarrays in a sorted manner until we are left with just one array. Here’s how the merging is done. We take two sorted subarrays, with a pointer at the left end of both subarrays. We keep adding whichever value (as denoted by both the pointers) is the smallest, to the solution array (and hence incrementing the pointers) until all the elements in both the subarrays are traversed. The following graphic explains the merge step.

How Merging Works :

This final array will be the required, sorted array.

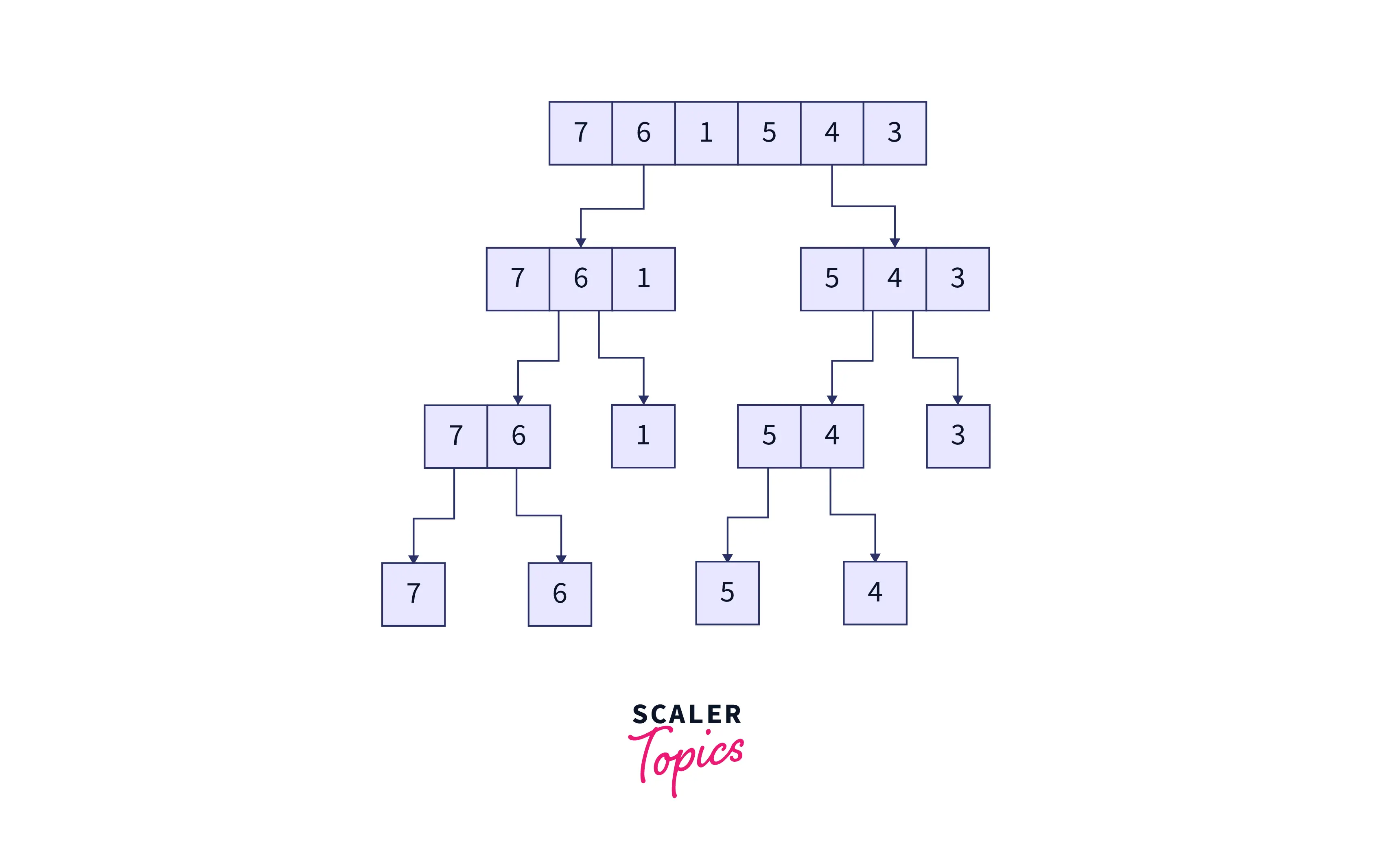
Arguably, since we are sorting and combining two sub-arrays at a time in this step, one can also say that this step involves conquer and merge stages of the divide and conquer algorithm running concurrently.

Now, let us perform the time-complexity analysis of the merge sort algorithm to find out how efficient this approach is as compared to other sorting algorithms like the bubble sort, insertion sort, etc.

Merge sort has primarily three kinds of operation, as we discussed earlier.

• Divide operation :
  The divide operation is a constant time operation $(O(1))$ regardless of the size of the subarray since we are just finding the middle index of the subarray $(mid = (start + end) / 2)$ and thereafter dividing the subarray into two parts based on this middle index. During the entire divide operation, we keep on dividing the initial array into 2 subarrays at each level, till we get subarrays of size 1. In total, there are going to be approximate $log2n$ levels of division operations.
• Conquer operation :
  As we discussed earlier, upon breaking down the initial array to sub-arrays of size 1, these sub-arrays get sorted by default. Hence, the conquer operation has a constant time complexity of $O(1)$.
• Merge operation :
  The merging operation at each level, where we sort and merge 2 subarrays at a time recursively, is a linear time operation, i.e., $O(n)$. As we discussed earlier, since there are $log2n$ levels in the division process, the merge step, on average, will take around $n.log2n$ steps.

Therefore, considering all three kinds of operations, merge sort results out to be an $O(n log2n)$ operation.

Comparing this to insertion sort or bubble sort, both of which have a quadratic time complexity of $O(n2)$, merge sort proves to be a relatively faster sorting algorithm, especially for large input sizes.

Thus, we understood how the divide and conquer algorithm works in practice. Next, let us compare the divide and conquer approach against the dynamic programming approach for problem-solving.

Divide and Conquer vs the Dynamic Programming Approach

When it comes to how a problem is tackled during problem-solving, both the divide and conquer as well as the dynamic programming algorithms share a common characteristic:

Before solving it, the initial problem is atomized into smaller sub-problems, and then the final output is generated in a bottom-up approach where the individual sub-problems are solved and their resultant outputs are merged into the final solution.

However, the difference between these two algorithmic approaches only becomes evident after the atomization or division step. The difference lies in how the sub-problems are solved and merged into the final solution.

When it comes to divide and conquer algorithms, as we saw earlier, the sub-problems are solved and merged recursively, without storing the results of individual sub-problem at each stage for any sort of future reference.

On the other hand, dynamic programming algorithms store the result of each sub-problem for the sake of future reference.

This distinction in the problem-solving approach of these two classes of algorithms originates from the use case of these algorithms in real-world scenarios.

• Divide and conquer algorithms are often used as single-shot solutions where we don’t require re-calculations on the same problem or sub-problem data. As a result, storing the keys of the individual sub-problems will just result in the wastage of memory resources.
• On the other hand, we use dynamic programming algorithms when we tend to require the solution of the same sub-problems multiple times in the future. Thus saving the output for future reference will save some computation resources and help eliminate redundancy.

Let us take an example that will help us visualize the difference better. We will consider a problem where we want to find the nth Fibonacci number in the Fibonacci sequence.

Divide and conquer algorithm :

The above-given solution is based on the divide-and-conquer algorithmic approach. For every nth Fibonacci number in the Fibonacci sequence, we keep breaking it down as the sum of $(n-1)th$ and $(n-2)th$ Fibonacci numbers. This breakdown keeps occurring recursively until we reach the base case $(i.e.$,index $n = 0$ or $n = 1)$. After reaching the base cases, we keep solving the individual subproblems and merging their solutions till we get the final solution, which is the nth Fibonacci number. The following example for deriving the 4th Fibonacci number will help us understand things better.

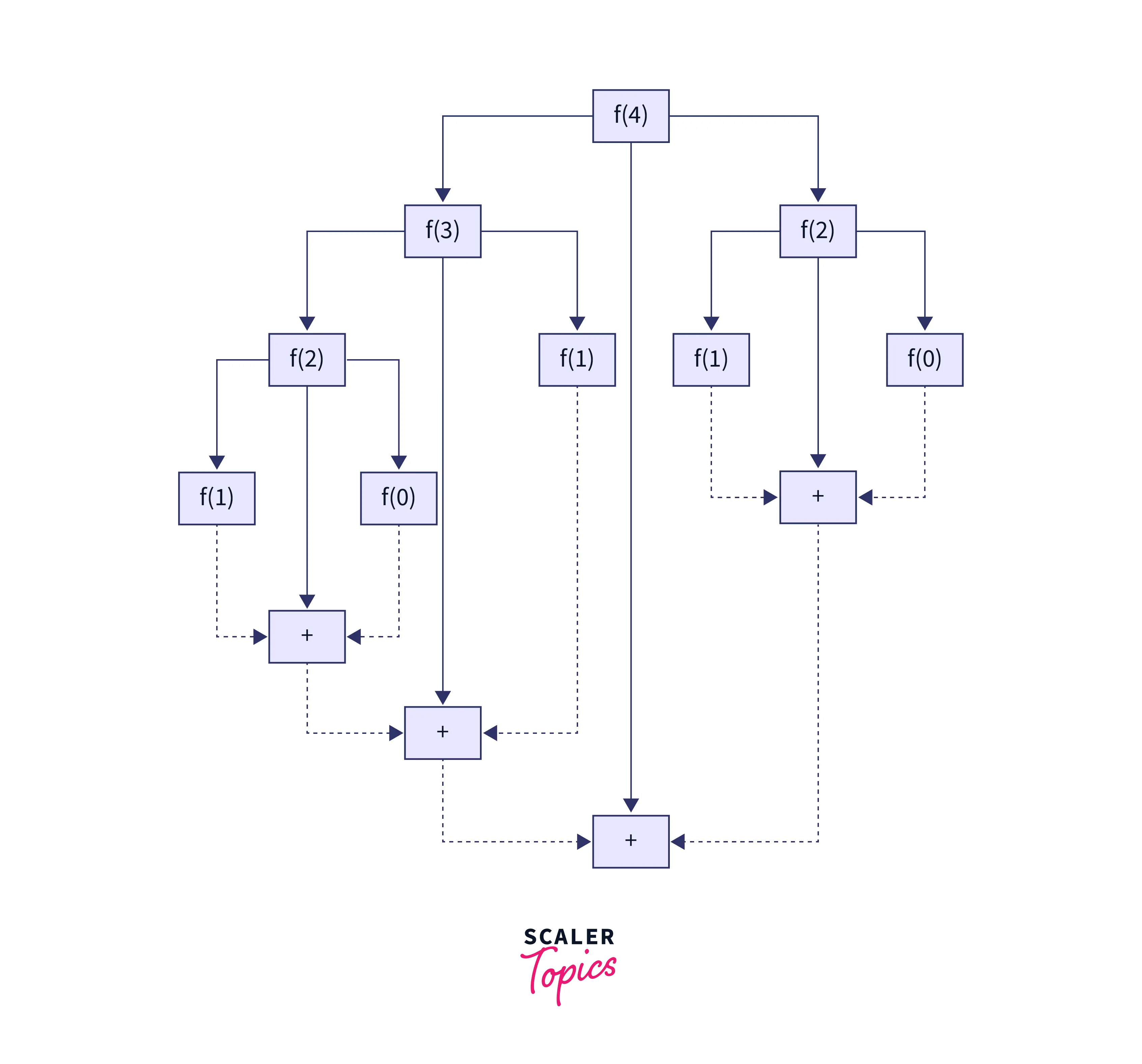
As you can see in the solution above, we aren’t storing any individual sub-problem results.

Dynamic programming algorithm :

In the solution given above, we are storing the result of each sub-problem in the memory array. These stored solutions can then be referenced and reused in the future as we are further solving the problem. This saves us some repeated calculations down the line.

So now that we know how the divide and conquer algorithms work and how they differ from dynamic programming algorithms, let us now take a look at the advantages that the divide and conquer algorithms provide over the other classes of algorithms.

Advantages of Divide & Conquer Algorithms

For some specific problem types, divide and conquer algorithms are known to render better efficiency as compared to their other counterparts. It is important to understand which areas the divide and conquer algorithms tend to perform better in so that when it comes to problem-solving, we can leverage their potential efficiently.

Therefore, let us discuss some advantages of divide-and-conquer algorithms.

• For sorting the values in an array, merge sort and quicksort are two of the fastest known sorting algorithms with the average-case time complexity of $O(n log2n)$. Both these algorithms are based on the divide and conquer algorithmic approach. Upon head-to-head comparison with sorting algorithms like insertion sort or bubble sort $($time complexity $= O(n2))$, an array of 1M elements $(106$ elements$)$ will require around 19.9M $(roughly 2 × 107)$ steps on an average to sort using quicksort. On the other hand, bubble sort will take around 1012 steps, which is a massive computation difference.

• The brute force approach of matrix multiplication is an $O(n3)$ operation, which is computationally very expensive. On the other hand, using a divide and conquer approach for the same (eg.- by using Strassen's matrix multiplication), this time complexity can be reduced to $O(n2.8074)$. Comparing this to matrices with a million elements (106 elements), this operation will take around 1018 steps for the brute force method, which is significantly higher than the roughly $7 × 1016$ steps required for the divide and conquer approach.

• For other problems too like the famous Tower of Hanoi or searching an element within a sorted array, the divide and conquer approach is known to give the optimal solution.

• Divide and conquer algorithms are known for making efficient use of memory caches, and are suitable for multi-processing systems.

Finally, now that we are well aware of some of the advantages of the divide-and-conquer paradigm, we’ll go ahead and take a look at the application of these algorithms in the field of computer science.

Application of Divide & Conquer Algorithms

Here are some of the most common applications of the divide-and-conquer algorithmic approach.

• Binary Search :
  Binary search is a search-based algorithm that follows the divide and conquers approach and can be used for searching a target element within a sorted array. While searching for an element within an array, binary search divides the array into two halves at each step, discarding one of the halves based on the value of the middle element. The algorithm can search for the target element with an $O(log n)$ time complexity, as compared to the $O(n)$ complexity in linear search.

• Merge Sort :
  Earlier, we saw the working of merge sort, which is a divide and conquer-based sorting algorithm, with the worst-case time complexity of $O(n log2n)$.

• Quick Sort :
  Quick sort, as we saw earlier, is another divide-and-conquer-based sorting algorithm that is often regarded as one of the fastest sorting algorithms, especially for large array sizes.

• Strassen's Matrix Multiplication :
  While dealing with matrix multiplication for large matrix sizes, Strassen’s matrix multiplication algorithm tends to be significantly faster as compared to the standard matrix multiplication algorithm.

• Karatsuba Algorithm :
  The Karatsuba algorithm is a highly efficient algorithm for the multiplication of n-bit numbers. It is a divide and conquers algorithm that performs the multiplication operation with a time complexity of $O(n^{1.59})$ as compared to the $O(n^2)$ of the brute force approach.

Apart from the above-mentioned algorithms, there exist several other algorithms within the divide and conquer paradigm too that can be used to solve a multitude of problem types.