Doubly Linked List

Introduction to Doubly Linked List

As you can guess, Doubly Linked List is an enhancement done on top of Linked List Data Structures. I would suggest going through the Linked List concepts before jumping ahead with Doubly Linked List.

But to summarise, say we have 3 elements,
If we go with Arrays, those will be represented as {1, 2, 3} Whereas in Linked lists, each element has a pointer to next element, so linkedList would be
represented as: 1 → 2 → 3 → Null It comes with its own advantages and disadvantages over Arrays, and are covered in detail in the above Linked Document.

In a linked List, we have a head node, which points to the first Node in the Linked List, and then we have the Null at the end, marking the end of the Linked list, as shown above. To transverse the list completely, we need to start from the head till the Null.

If you would look carefully, in any LinkedList, it is not easy to go to the previous Element. E.g. if we have a LinkedList = 1 → 2 → 3, then we can traverse it from 1 to 2 and from 2 to 3, following the Next pointers, but what if we want to go back to 1 from 2?

Unfortunately, in such scenarios, there is no easy such way out in linked Lists, and the only thing we can do is to iterate the LinkedList from start and keep moving ahead until we see the the next of current element = 2, here 1 → 2, so we would know that previous of 2 is 1.

And consider the time it would take if we need to find the previous element of the 1000th Element in the LinkedList. We basically need to iterate from the 1st element, up until the 999th Element to find such an element. And this is not good.

So to tackle such complexities in the LinkedList where we need to transverse in both directions, we can use Doubly Linked Lists.

What is Doubly Linked List?

Doubly Linked List is a Data Structure, which is a variation of the Linked List, in which the transversal is possible in both the directions, forward and backward easily as compared to the Singly Linked List, or which is also simply called as a Linked List.
You might be aware of the Tabs in Windows/Mac. You can basically loop over all the opened applications, and can switch between these applications in both the directions.
This can be thought of as all these Applications are linked via a Doubly Linked List Data structure, and you can switch to the applications on both sides of the current application.

So if a Linked List ⇒ A → B →. C
Then a Doubly Linked List ⇒ A ⇆ B ⇆ C

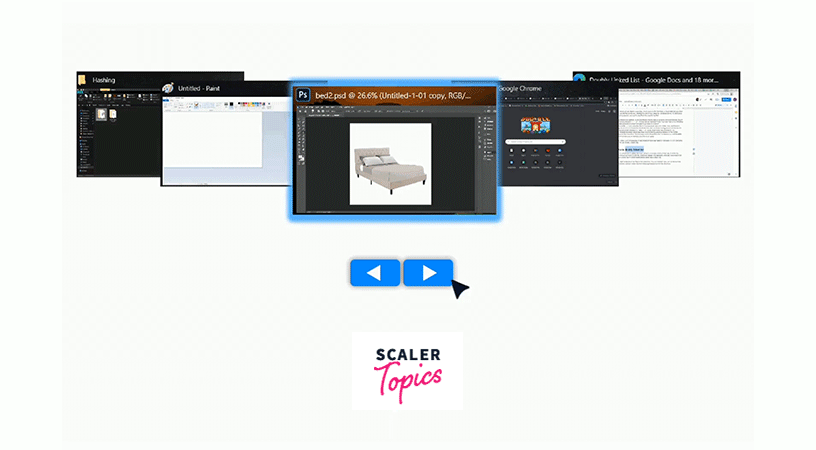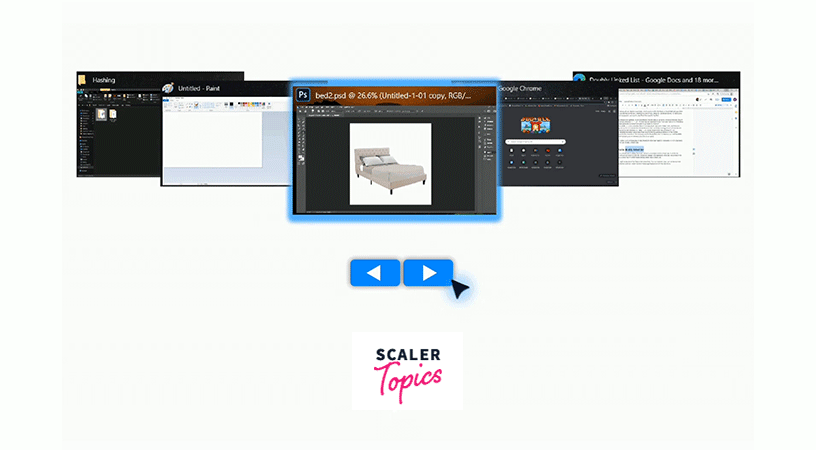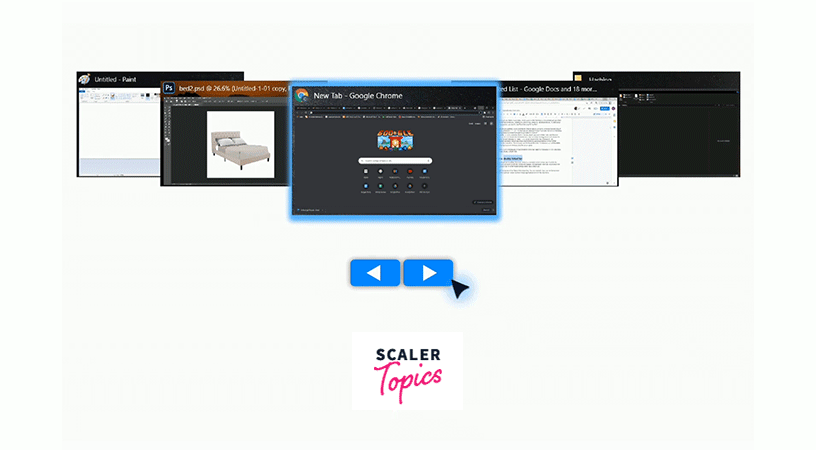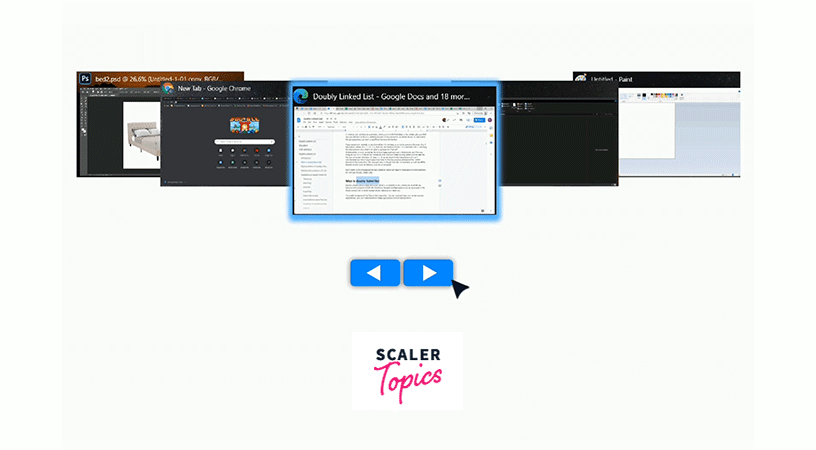
Representation of Doubly Linked List in Data Structure

If you can recall how the Linked List was represented using 2 parts: Value and the next pointer.
The Doubly Linked List has 3 parts: Value, Next pointer, and the Previous pointer.

The Previous pointer is the fundamental difference between the Doubly Linked List and the Linked List, which enables one to transverse back also in the Doubly Linked List.

As per the above illustration, following are the important points to be considered.

• Each Doubly Linked List Element contains pointers to next and Previous Elements and the data field.
• The First Element will have its Previous pointer as Null, to mark the start of the List.
• The Last Element will have its Next pointer as Null, to mark the end of the List.

From the Code Perspective, the Doubly Linked List can be represented as:

We also use the concept of “head” node, which points to the first Node in the Doubly Linked List. Using the head node we know where the Doubly Linked List starts from.

Memory representation of a Doubly Linked List in Data Structure

A Doubly Linked List is represented using the Linear Arrays in memory where each memory address stores 3 parts: Data Value, Memory address of next Element and Memory Address of the previous Element.
This can be picturised as:

In the above image, -1 is being used to represent NULL.

Here 1000, 1051, 1052 etc represents the addresses in the memory, and we traverse the Doubly Linked List until we find -1 in the Next of the Node. This Memory representation shows that the Values need not be stored contiguously.

As shown above, Element A has previous = -1 i.e. NULL, so it is acting as the first Node in the Doubly Linked List.

A’s Next points to memory address 1052, where B is stored, so this represents that B is to the next of A. Similarly B’s Next has a memory address of 1059 where C is stored.

Similarly D has its Next as -1, meaning its the last Node of this Doubly Linked List.
So it forms the DLL like: -1 ← A ⇆ B ⇆ C ⇆ D → -1.

Operations on Doubly Linked List

Traversing

Since the Doubly Linked List has both next and previous pointers, this allows us to transverse in both the directions from the given Node.
We can go to the previous node by following the previous pointer, and similarly go to the next nodes by following the next pointers.

Transverse from B:

And Transverse Back from C:

Algorithm:

Searching

To search in the given doubly linked list, we would basically need to traverse the entire doubly linked list from the first node, and keep moving to next nodes using the next pointer. We can compare each transversed element against the one we are searching for.

Please note that this is the same as the Singly Linked List searching algorithm.

Insertion

Insertion into the Doubly Linked List is fast and can be done in constant times, as we just need to change the pointers of adjacent elements we are inserting this element between.

We will see how this works in the below sections, but one thing to note is that like Linked List, insertions are faster in Doubly Linked List over Arrays, as here we need to shift any elements forward, and hence it takes Constant time to insert.

E.g. if Array = {1, 2, 3} and to insert 10 at 1st Index, we need to move 2 and 3 one step forward to make space for 10, to get: {1, 10, 2, 3}
But this shifting of rest of the elements is not required if the inserting is to be done inside the doubly linked list.

There can be 4 different ways of inserting a new Element inside a Doubly Linked List, and we will see each of these ways in detail below:

Insert First

A Node can be inserted as the first element in the Doubly Linked List.
Earlier Doubly Linked List: A ⇆ B ⇆

Now after we insert X inside this Doubly Linked List: X ⇆ A ⇆ B ⇆ C

So as we can see, to insert an element at front, we need to change pointers of A Node.

Earlier: Head points to A and A.previous points = NULL.

After Insertion:

X.previous points to NULL, and X.Next points to Head or to A.

Update A.previous = X.
Update Head to now point to X.

As we can see, we are only updating the pointers of adjacent Nodes, so it takes Constant time to insert a new Element at the front of the Doubly Linked List.

Insert After a Node

If we are given a Node(say C) and we want to insert a new Node(say X) after it, then the algorithm would look like:

DLL Before ⇒ B ⇆ C ⇆ D ⇆ E

After Insert X after C⇒ B ⇆ C ⇆ X ⇆ D ⇆ E

So as we can see, we need to change :

C.next to now point to X.
D.Prev now points to X.
And X.prev points to C and X.next points to D.

As we can see, we are only updating the pointers of adjacent Nodes, so it takes Constant time to insert a new Element after a given node in the Doubly Linked List.

Insert Before a Node

If we are given a Node(say C) and we want to insert a new Node(say X) before it, then the algorithm would look like:

DLL Before ⇒ B ⇆ C ⇆ D ⇆ E
After Insert X after C ⇒ B ⇆ X ⇆ C ⇆ D ⇆E

So as we can see, we need to change :
C.prev i.e. B has its Next changed to X.
C.prev to now point to X.

And X.prev points to B and X.next points to C.
But there is another scenario, what if there was no B? I.e. C was the first Node. In that case head will now point to X instead of C.

As we can see, we are only updating the pointers of adjacent Nodes, so it takes Constant time to insert a new Element before a given Element of the doubly linked list.

Insert last

If we want to insert a new Node(say X) at the end of the Doubly Linked List, then the algorithm would look like:

DLL Before ⇒ A ⇆ B ⇆ C
After Insert X at end ⇒ A ⇆ B ⇆ C ⇆ X

So as we can see, we need to change :
C.next is changed to X from Null.
And X.prev points to C and X.next points to Null.

Algorithm:

This has 2 other scenarios to handle:

1. If the Doubly Linked List is Empty, then X must be a new Node which will have both prev and next pointing to null. And Head should now point to this new Node X.
2. To find the last node, we need to iterate the doubly linked list from the start. Once we find the last node i.e C, then we can insert X after it.

As we can see, to insert the new node at the end of the Doubly Linked List, we might need to transverse the entire list, so this Insertion would take O(N) time, as we would need to transverse all the N nodes in the Doubly Linked List.

Deletion

Similar to Insertion, deletion in a Doubly Linked List is also fast, and can be done in Constant time by just changing the pointers of its adjacent Nodes.
We will again see some ways of deleting the Node below:

Delete any Given Node

To delete the Node if its the last node in the Doubly Linked List:

DLL Before: A ⇆ B ⇆ C
DLL After Deleting B: A ⇆ C
By updating A.next to C and C.prev to A.

Lets see the algorithm first and understand what all scenarios can it cover:

Lets see if this can handle the 3 different scenarios:

Scenario 1: Node to Delete = Head node i.e. A

Then earlier Head points to A, and after A is deleted head points to A.next i.e. B.
B.Previous earlier pointed to A, and after A is deleted B.previous should point to Null or A.previous which was Null.
This is taken care of in 2nd and 3rd If blocks.

Scenario 2: Node to Delete = Last node i.e. C

Then earlier B → C, and after C is deleted B → null as now B becomes the last Node.
This is taken care of in the 4rd If block.

Scenario 3: Node to Delete = anywhere in between the Doubly Linked List:

If we want to delete B,
And Update C to point to B.previous i.e. A.
This is handled in the 3rd If Block.
Update A to point to B.next i.e. C
This is handled in the 4th If block

As we can see, first if condition handles the base Null cases.
Second If handles the case where NodeToDelete is the head node.
Third If handles the case where NodeToDelete lies anywhere in between the Doubly Linked List and takes case of
Fourth If handles the case where NodeToDelete is the last Node.

NOTE - The deletion is faster than a Singly Linked list as to delete a Node in a Singly Linked list e.g. A → B → C → D, and say we want to delete C.

Then we need to set B → D. But when we want to delete C, we won't have a pointer to B to update it next to D. So to delete C in the Singly Linked list we would need to traverse the list from start to reach B, and then update B.next=D.

But in case of Doubly Linked list, we can get the pointer to B directly using the C.previous pointer, and it prevents the transversal from the start.

Delete a Given Position

If instead of the nodeToDelete, a position is given at which we want to delete the Node, then unlike in Arrays we don’t have a random access to a given pointer inside the doubly linked list.

So in a doubly linked list we would basically need to transverse till this position, retrieve the Node at that Index, and can then call the above delete method passing in the node we want to delete.

So as we can see, to delete a Node at a given position, we need to transverse till a given position and then delete it by updating the pointers of its adjacent elements.

Since transversal takes O(N) time to transverse till Nth element, deletion at a given index is a costlier operation than in arrays, where we know which element exists at a given index directly.

See Also

1. Doubly Linked List in C
2. Doubly Linked List in C++