Euclidean Algorithm for GCD
Learn via video course

Overview
The formula for computing GCD of two numbers using Euclidean algorithm is given as GCD (m,n)= GCD (n, m mod n). It is used recursively until zero is obtained as a remainder.
Takeaways
- Complexity of Euclidean algorithm
- Time complexity - O(log(min(a, b)))
Introduction
Imagine while remodeling your house, for some reason, you want to cover an entire floor with the minimum number of square-shaped tiles such that these tiles are all equal in size.
Naturally, the question begs, what sized tiles do you ought to pick? 🤔
As human beings, we can often intuitively arrive at a solution when the problem is simple enough. However, in not so simple scenarios, we might want to leverage an Augmented Reality application to do the job for us.
Have you ever wondered what kind of algorithm we might need for developing such apps in the first place?
In our case, it turns out that such an algorithm already exists. And it is known as the Euclidean Algorithm! 😇
The Euclidean algorithm efficiently calculates the greatest common divisor (GCD) of two non-negative integers. By finding the GCD, it helps solve various problems like cutting square towels from a rectangular cloth or placing square tiles on a rectangular floor. The algorithm's intuition reflects the manual method we used to find the GCD by hand, making it a reliable and efficient tool.
Basic Euclidean Algorithm for GCD
Given two non-negative integers, a and b, the Euclidean algorithm states that the GCD(a, b) can be described as follows:
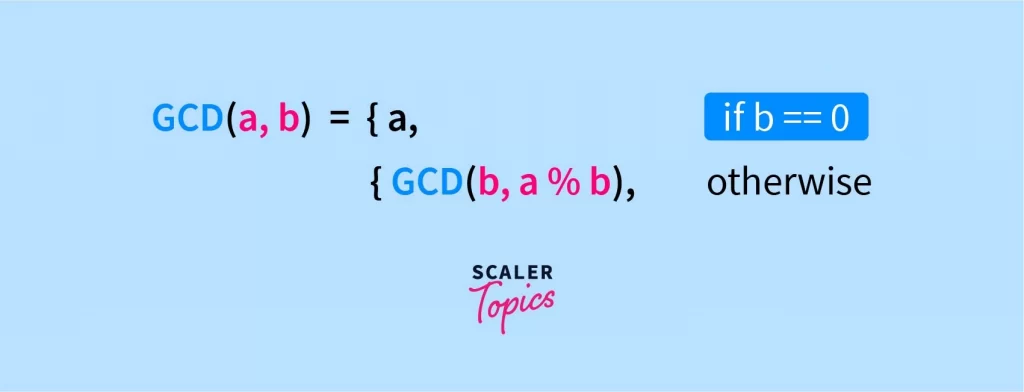
Here % denotes the modulus operation, and GCD(a, b) refers to the largest integer that divides both a and b without any remainder.
In order to make the above Euclidean algorithm complete, we must enforce an additional constraint, GCD(a, b) <= min(a, b). 🔐
Take for example, a = b = 0. Then, without the above constraint, any arbitrarily huge number can divide zeros. Think about it, 17 can divide both a and b without any remainder, but so can 1237829 and a Googleplex!
So, if we had a floor of size 0 x 0, then fitting an infinitely huge tile in that space doesn’t make sense now, does it?!!
That’s why the GCD of two non-negative integers should be at most equal to the smaller of the two.
The implementation of the above Euclidean algorithm in C and C++ is pretty straightforward due to its recursive nature;
Also, a one-liner Python implementation of Euclidean Algorithm would look something like this;
Here’s a Java implementation;
In all the cases, gcd is a function that takes two non-negative integers a and b and calls itself recursively.
Now, I could go on with various language-based implementations, but we still haven’t explored why the Euclidean algorithm works! 🪄
So, let’s build on that intuition…

Example of the Euclidean Algorithm
We’ll expand upon our previous example of choosing a tile so as to minimize the required number of such tiles to cover a given floor. Imagine, we have an infinite supply of square shaped tiles of all sizes starting from 1 x 1.
Excluding igloos, I would say most houses have a rectangular floor. So let’s assume the length as 6 units and breadth as 4 units.

We can always fit 1 x 1 tiles irrespective of the length and breadth, but that would maximize the required number of tiles to around 24.

Let’s do better.
How about 2 x 2 tiles? In this case, we only need 6 tiles to cover the entire floor. Much better.

Let’s keep going and check for 3 x 3. Unfortunately, we are unable to fit all 3 x 3 into our given floor. And it turns out that 2 x 2 is the best we could do while following all the constraints.
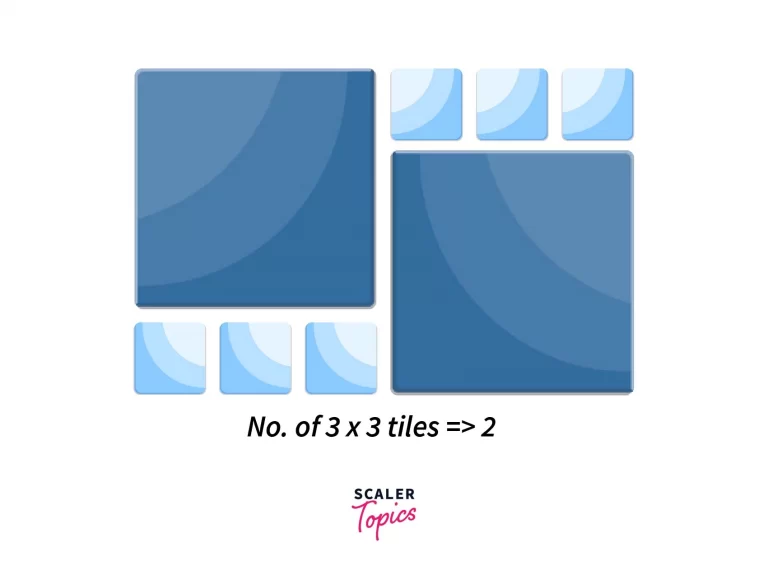
Since we’ll never be able to fit 5 x 5 or 6 x 6 sized tiles into a space of 6 x 4, the checks would stop at around 4 x 4.
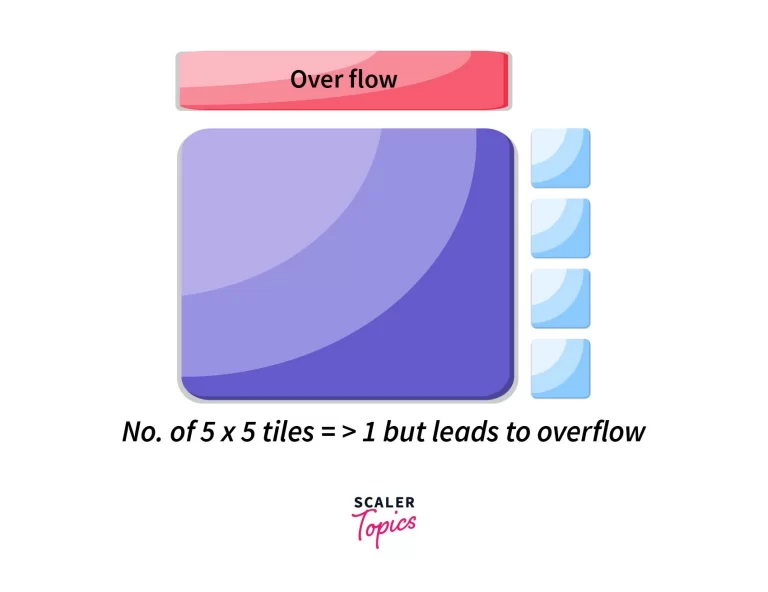
Hence the brute force would look something like this,
Basically, we check for perfect divisibility of both numbers considering all divisors starting from 1. And, since our search for the divisor starts from the minimum value, the last divisor that divides both numbers perfectly would also be the greatest common divisor.
In the end, "ans" holds this greatest common divisor, which in our case happens to be 2. More formally, GCD(6, 4) = 2.
And the time complexity of the above approach becomes O(min(a, b)) since we are only exploring until the smaller of two integers a and b.
Now, the Euclidean algorithm improves this time complexity by having a more noble insight. 💡
The intuition would sound something like this – if we want to minimize the number of tiles required, we should first try to maximize the size of the squared tile without overflowing.
In our case, a 4 x 4 tile is the biggest tile that can fit inside a 6 x 4 floor. Mathematically, it originates from the fact that min(6, 4) = 4.

Now the leftover space is 4 x (6 - 4) = 4 x 2. Notice it’s four times two. I repeat FOUR times two.
So, think about it, if we can fit certain sized tiles perfectly in our leftover space then it guarantees that the side of those tiles divides 4 and 2 perfectly.
Because, if it doesn’t, then the problem again reduces to finding the maximum tile we can fit in 4 x 2, and we can simply repeat the procedure recursively.
Fortunately, in our case, there exists a tile of size 2 x 2 (since min(4, 2) = 2) that divides both 4 and 2. Naturally, those tiles can fit the leftover space like so,

Notice our previous space was 4 x 4, implying that square tiles of 2 x 2 can also fit inside the previous space because we just saw it can divide 4.

Therefore the answer to our original problem is a 2 x 2 tile. In other words, GCD(6, 4) = GCD(4, 2) = GCD(2, 0) = 2.
Let’s take another example of the Euclidean Algorithm to drive the point home, a = 21 and b = 13. But this time give it a shot and try to find the GCD of a and b by hand.
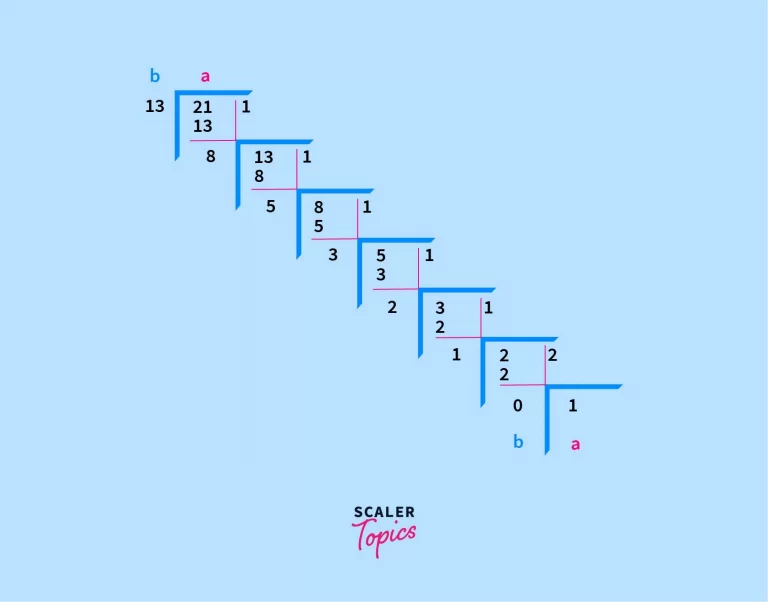
In every step, we are considering the current remainder as the next divisor, and the current divisor as the next dividend, like so;
b' = a % b
You see, we used to leverage the Euclidean algorithm during high school without even realizing it.
In the end, remainder zero signifies that the last divisor 1 divides both 21 and 13. And it just happens to be the greatest as well as the only such divisor in this case.
That’s why the base case b == 0 returns a, the leftover space is calculated by the remainder of a division, and that’s why the Euclidean algorithm looks the way it looks,
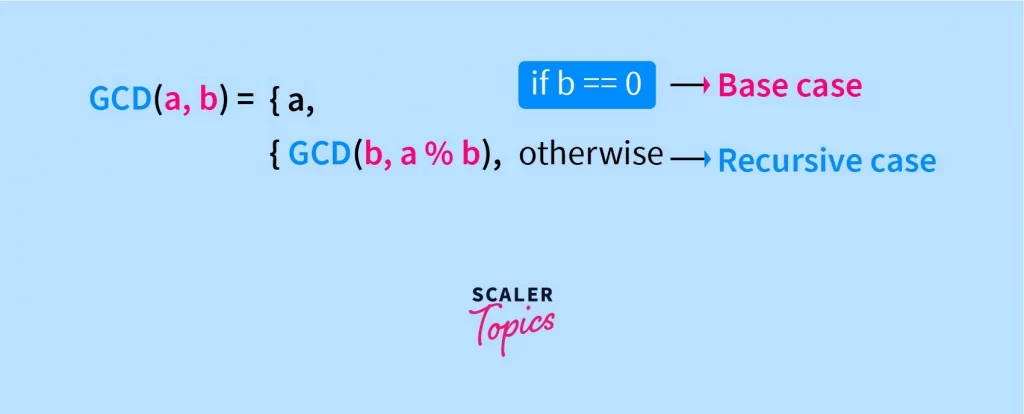
At every step, a becomes b, b becomes a % b, and in the end, b == 0 signifies "perfect divisibility" vis-a-vis "no leftover space" in the context of a floor.
Time Complexity of the Euclidean Algorithm
Let’s assume we are interested in finding the GCD of two non-negative integers, a and b (where a > b).
For every recursive step a, b => b, a % b, we have two possibilities:
- b >= a / 2
- In this case, the next b’ (= a % b) becomes at most half of the previous a, i.e.
0 <= b’ < a / 2
- In this case, the next b’ (= a % b) becomes at most half of the previous a, i.e.
- b < a / 2
- In this case, the next a’ (= b) becomes at most half of the previous a, i.e.
0 < a’ < a / 2
- In this case, the next a’ (= b) becomes at most half of the previous a, i.e.
So at every step, the Euclidean algorithm divides at least one number by 2. Do you know the kind of function that does the exact same? Logarithmic functions. Hence, a loose upper bound of our algorithm in terms of time can be estimated as O(log(a)) + O(log(b)) => O(log(a*b)).
Now, if we consider a and b as consecutive integers in the fibonacci sequence, like so,
and F(i) denotes the ith number in the sequence formed by F(i) = F(i - 1) + F(i - 2)
Then, it is possible to show that the algorithm performs n - 2 recursive calls assuming the sequence starts from F(1) = 0 and F(2) = 1.
Also, I can assure you this scenario of consecutive fibonacci integers would always be the worst case for GCD. You can check it yourself for the example GCD(21, 13) we discussed earlier.
21 and 13 are the respective 9th and 8th terms of the fibonacci sequence, and so the total recursive steps become (since n = 9)
This relation between the fibonacci sequence and the Euclidean algorithm was established by Lame’s theorem and I am just saying this if you want to explore further nitty-gritty heuristics.
So, without further ado, let’s unveil the time complexity of the Euclidean algorithm to be O(log(min(a, b))). Indeed, a much tighter upper bound than our previous O(log(a * b))!
But how did we arrive at this O(log(min(a, b)))?
Well, the fibonacci sequence grows exponentially, i.e. log(b) ~ n since b is the (n - 1)th term. Initially, we assumed a > b, so for accounting both cases, we take the minimum of a and b, hence (n - 2) recursive calls ~ log(min(a, b)).
Remember this was always the worst case in consideration, hence the time complexity is O(log(min(a, b))).
And that’s it! That’s all there is to the basic Euclidean algorithm which brings us to our conclusion… 🤗
Conclusion
- To sum it all up, the Euclidean algorithm helps us in finding the greatest common divisor of two non-negative integers.
- It also goes beyond just calculating the GCD and to explore more about that, please check out the article on the Extended Euclidean Algorithm.
- The Euclidean algorithm is not the only way for calculating GCD. There exist two other methods, namely,
- The “easy” method: Inspection
- Prime Factorization Method
- To conclude, a wise fellow once said,
- “Give a man the theory of the euclidean algorithm, and he forgets in a day;
- show a man where to practice, and he retains for a lifetime!”
- Here are a couple of problems for you to practice:
- The Euclidean algorithm is one of the most prevalent algorithms in n umber theory, and I hope you understood it well!
