Fenwick Tree | Binary Indexed Trees

Introduction to Fenwick Tree

When answering to multiple prefix sum (sum of array elements from 0 to an index $x$ $i.e.$ $a[0]+a[1]+...+a[x]$ queries of an array, the first idea that comes to our mind is to use a prefix_sum array.

For Example:

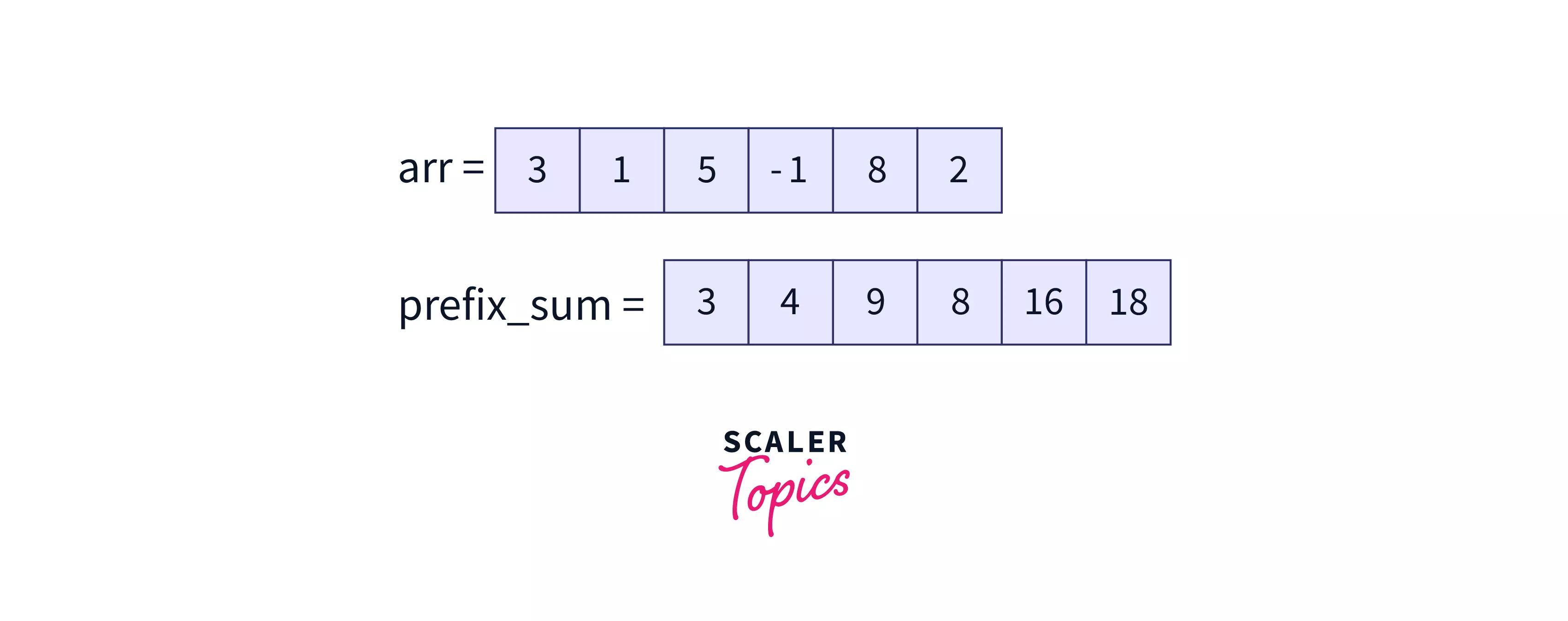
Here if we want to calculate $a[0]+a[1]+...+a[4]$, we do not need to calculate it instead we can simply return _prefix\_sum[4]_ as it already contains the sum of those values.

Also, if we want to calculate the sum of a segment of the array,

For Example: $a[2]+a[3]+a[4]$ then instead of calculating we can return prefix_sum[4]$-$ prefix_sum[1].

That means we can answer all such queries in constant time, but if we also need to update array elements frequently then, using prefix_sum array would be of no use because in case of updation we may need to re-construct the whole prefix_sum array.

In such cases, Binary Indexed Tree comes into the picture. A binary indexed tree popularly known as the Fenwick tree is a data structure that maintains the cumulative frequencies of the array elements at each of its nodes.

One of the best and simple use cases can be calculating the prefix sum of an array in which values are mutable (i.e. values can be changed) logarithmic time complexity.

Basic Idea of Fenwick Tree

If we want to calculate prefix_sum of array $a$ of size $n$ then we will use another array $(bit)$ of size $n+1$ ($n+1$ is to maintain 1-based indexing for simplicity).

The basic idea behind Binary Indexed Tree is that we can store the sum of a particular range of elements at an index of the newly formed $bit$ array. Which will be used later to calculate prefix_sum in the fewer number of steps.

The idea that "every integer can be represented as the sum of powers of 2" is used extensively in the formation of the Fenwick tree. Using this fact we can calculate the _prefix\_sum_ of an array in logarithmic time complexity.

Representation of Fenwick Tree

The BIT (Binary Indexed Tree) is represented as an array (say $bit$). Where each index of $bit$ stores the sum of a range of elements of the original array (say $a$).

Let $i$ be an index of the array $bit$, then $bit[i]$ will contain the sum of elements KaTeX parse error: $ within math mode where $x$ is the position of the least significant set-bit in the binary representation of $i$.

Let us understand by an Example: Let's say we want to know the range of which sum is stored in $bit[12]$, we know that binary representation of $12$ is $1100$, we can see that the position of least significant set-bit from right, $x$ is $3$.

That means $bit[12]$ will contain the sum of the range $(13-2^{3-1}+1) \rightarrow 12$ $i.e.$ $9 \rightarrow 12$.

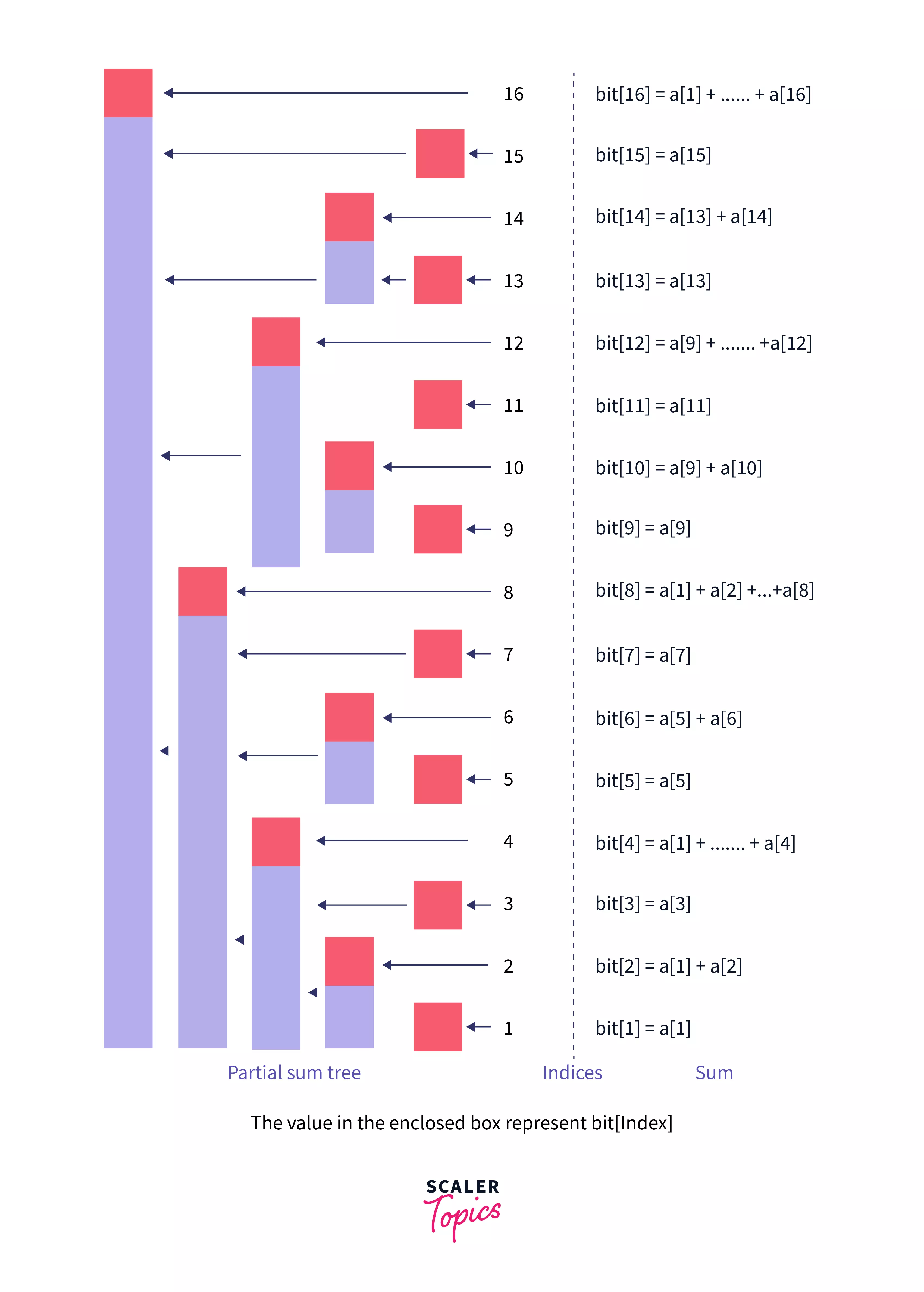
The above image represents the range of elements for which the sum is stored for any index i in the bit array of size 16.

For Example: index 12 in bit holds the sum of the values of the range $[9\rightarrow 12]$ present in a and index 8 in bit holds the sum of the values of the range $[1\rightarrow 8]$ in a. So to find the prefix_sum[12] we can simply find $bit[12]+bit[8]$ instead of calculating sum one by one.

Operations of Fenwick Tree

The two main operations supported by Fewick tree are -

• getSum(x) - This operation returns the sum of first $x$ elements of the array $i.e.$ $a[0]+a[1]+...+a[x]$.
• update(x,val) - This operation updates the value of $a$ at index $x$ $i.e.$ $a[x]=val$

We can also find the sum of any arbitrary range $[left,right]$ using the below-given function which uses getSum(x) to find the same.

getSumRange(left, right): This operation returns the sum of array elements within a range $i.e.$ $a[left]+a[left+1]+...+a[right]$. It can be easily calculated using _getSum(x)_ operation by returning getSum(right+1)-getSum(left)

How does Fenwick Tree Works?

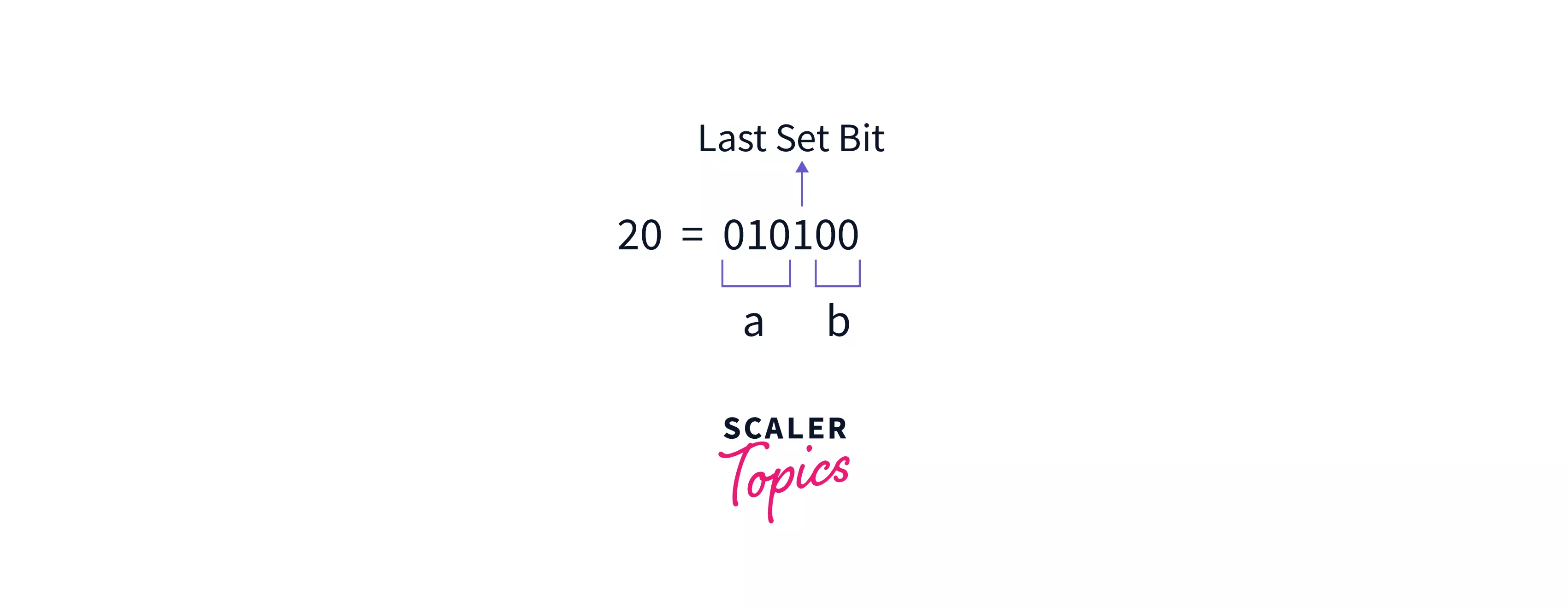
Before getting into the actual working of the Binary Indexed Tree (Fenwick Tree), let's first see we can find the least significant set-bit of any integer, say $x$. This is a very crucial step because it plays a key role in implementing the Binary Indexed Trees.

Finding the least significant set-bit of $x$

It is understood that for any $x>0$, we can express it in the binary form $a1b$, where $a$ is any arbitrary binary string consisting of both $1's$ and $0's$ and $b$ is a binary string of all $0's$ because $1$ is the last set-bit present in the binary representation of $x$. For example, the binary representation of $20$ is $010100$, if we write this in the form of $a1b$ then, $a$ will correspond to $010$ and $b$ will correspond to $00$.

We have studied that in binary form $(-x)$ represented as $2's$ complement of $x$ and $2's$ complement of $x$ is equal to $x'+1$. Now since $x=a1b$ $\implies$ $x'=a'0b'$, Since $b$ had contained all $0's$ so $b'$ will contain all $1's$. Adding 1 to $a'0b'$ will make it $a'1b$. Let's observe this phenomenon with the example of 20.

$x=(010100)_2$

Representing it of the form $a1b$ will give $a=010$ and $b=00$. $x'=(101011)_2$

We can clearly see now $b$ contains all $1's$, and it is of the form $a'0b'$ with $a'=101$ and $b'=11$. $-x=x'+1=(101011)_2+(1)_2=(101100)_2$

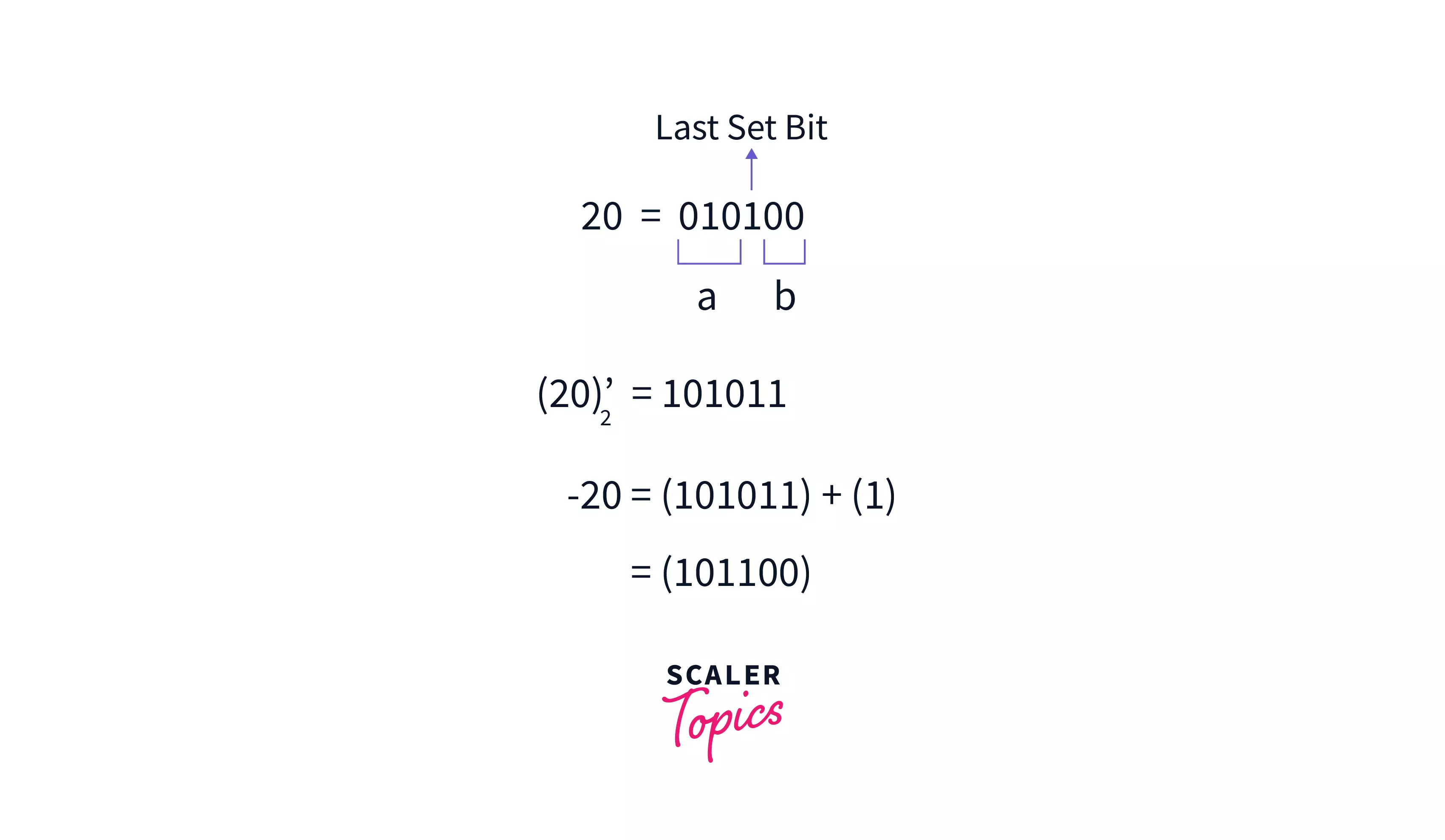
Hence it is of the form $a'1b$, now if take $and$ of $x$ and $-x$ we will get something of the form $(p1q)_2$ where $p$ and $q$ are binary strings with all $0's$ $i.e.$ a number with only one set bit because $a\&a'=0$ and $b$ was already zero.

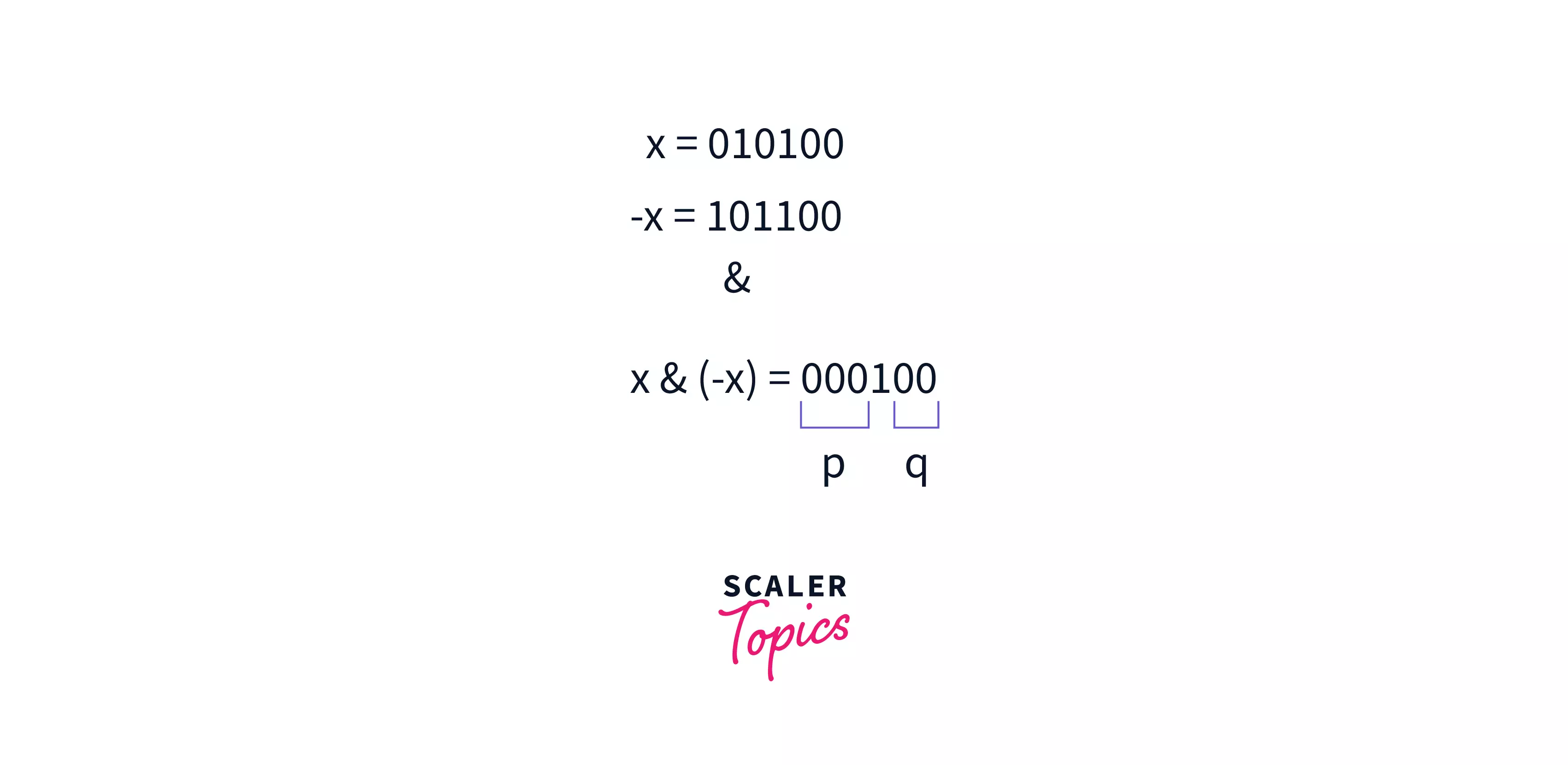
To remove the least significant set-bit from $x$ we can subtract the result obtained of $x\&(-x)$ from $x$.

For Example: $x=20$ and $x\&(-x)=4$ $\implies$ $x-(x\&(-x))=16$ which is the same number that could be obtained by removing the least significant set-bit of 20.

As discussed in the previous sections we will not be representing the Fenwick tree in a "tree like structure" instead we will represent it as an array of size $n+1$ for any given array of size $n$ to maintain 1-based indexing. Let bit be the array that represents the fenwick tree of size $n+1$. Then we can have the following operations on bit.

getSum(x) operation:

getSum(x) operation returns sum of array elements from $0^{th}$ index to $x^{th}$ index $i.e.$ $a[0]+a[1]+...+a[x]$. Steps invloved to calculate it are -

• Initialize answer, ans with 0.
• Increase x by 1 (To maintain 1-based indexing).
• While x is greater than 0
  • $ans+=bit[x]$
  • $x-=(x\&(-x))$
• Return ans

update(x, val) operation

update(x, val) operation updates the value of array $a$ at index $x$ to $val$. After updating, we also need to update $bit$ array at those indices which get impacted by the element at index $x$. , Steps involved in that are -

• Find the change happening at the index x, $\delta val=val-a[x]$.
• Update the value at index x $i.e.$ $a[x]=val$.
• While $x\leq n$
  • $bit[x]+=\delta val$
  • $x+=(x\&(-x))$

When to Use Fenwick Tree?

Fenwick tree is mostly used when we have been given an array (say $a$) and we need to answer multiple getSum queries $i.e.$ finding the sum of first $x$ elements many times or/and we need to find the sum of a range of elements many times, and also we need to perform multiple update operations $i.e.$ updating the value of $a$ at any particular index $x$.

Construction of Fenwick Tree

Let's say we have been given an array $a$, of size $n$. So we will create another array of size $n+1$(say $bit$) all of its entries will be initialized with 0. Then we will use the update function for each index of array $a$. Its pseudocode will be like -

For Example: Let $a=\{4,2,1,5,6,3,9,7,2,3\}$ Then $bit$ array will correspond to - $\{4,6,1,12,6,9,9 ,37,2,5 \}$ where $bit[i]$ represents sum of range $(i-2^{x-1}+1) \rightarrow i$

Implementation

To implement the Fenwick tree (BIT) we will have the following global variables to maintain simplicity in the code.

• n- It denotes the size of the array on which we want to perform certain operations which are discussed in the previous sections.
• bit- It is the actual binary indexed tree that is represented in array format. Its size will be n+1 to maintain 1-based indexing.

The functions which are needed to implement functionalities of the binary indexed trees are :

• FindSum- It takes one argument (say ind) and we need to return the sum of values of the given array (say a) in the range [0, ind].
• SumOfRange- It takes two arguments (say left and right) and we will return the sum of values of a in the range [left, right]
• Update- It takes two arguments (sat ind and val) and we need to change the value of a at index ind to val and correspondingly we also need to update the bit.

Pseudocode of Fenwick Tree Implementation

Fenwick Tree Implementation in C/C++

Fenwick Tree Implementation in Java

Output: Sum of range 2-6 is 24. Sum of range 5-9 is 33.

Applications of Fenwick Tree

Fenwick Tree is mainly used to optimize the process of finding the prefix sum of the arrays such that we can have the prefix sum of an array index in logarithmic time complexity. However, there are some popular questions that can be efficiently solved using Fenwick trees:

• Mutable Range Sum Queries: Q queries can be answered in $O(Q\times \log{n})$ time which is way better than $O(Q\times N)$ run-time of brute force approach.

• Count Inversions in an Array: The number of inversions can easily be found in $O(n\times \log{n})$ time even without sorting the array.

• Count smaller numbers after self: Many practical uses can be seen in the real world which can be computed efficiently using BIT.