Greedy Algorithm

What is the Greedy Algorithm?

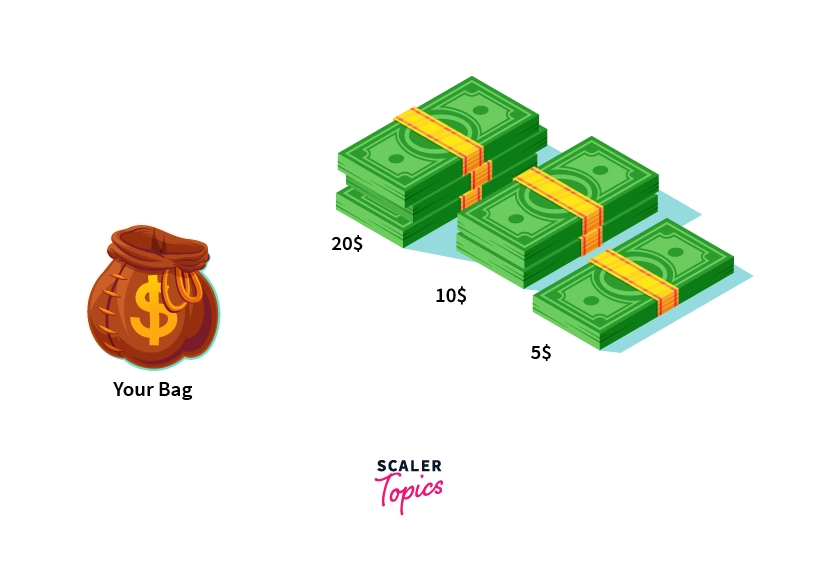
Now, to maximize the amount you take, you'll obviously start with the $20 pile. If you're able to finish that pile in under one minute, then you'll move to the $10 pile (and not the $5 pile). If you're extremely fast here too, then finally you'll go for the $5 pile.

This is an example of the greedy approach. To maximize the amount of money you take, you start with the most desirable solution at that point of time. You don't worry about whether this choice will hurt your profit in the coming future.

A greedy algorithm refers to any algorithm employed to solve an optimization problem where the algorithm proceeds by making a locally optimal choice (that is a greedy choice) in the hope that it will result in a globally optimal solution.

In the above example, our greedy choice was taking the currency notes with the highest denomination.

Please note:

1. The greedy solution to an optimization problem is very intuitive sometimes, but more often than not, it does not yield the globally optimal solution.

   For example, in the example discussed above, it just felt right that we choose the notes with the higher denomination to maximise our profit. Lucky for us, it worked!

2. Hence, it is always advisable to prove the correctness of the greedy algorithm before using it to solve the problem at hand.

3. As intuitive as it is, it is not always easy to prove mathematically that the greedy algorithm will lead to the globally optimal solution.

Some common algorithms and protocols that use a greedy approach are:

1. Prim-Jarnik's and Kruskal's Minimal Spanning Tree (MST) algorithms
2. Djikstra's Shortest Path algorithm
3. Activity selection problem
4. Huffman Coding (used for lossless data compression)
5. Open-Shortest-Path-First routing protocol (it uses Djikstra's algorithm)

Characteristics of the Greedy Algorithm

1. Any greedy algorithm consists of a sequence of choices/ decisions (for the problem we're solving) and each choice made should be the best possible one at the moment
2. The choice made at any point cannot be altered later.
3. The greedy algorithm may not always yield the globally optimal solution and may even result in the worst global solution (such as in the Travelling Salesman Problem).
4. Greedy algorithms are very fast as compared to their alternatives, such as dynamic programming. This is because dynamic programming has to consider all possible cases locally at all times, while the greedy approach goes ahead with only one optimal choice.
5. Greedy algorithms are very intuitive, but it is very hard to prove mathematically the correctness of the algorithm.
6. The greedy algorithm may lead to a solution that is very close to the optimal solution in problems where there is no efficient solution. It is to be noted that the obtained solution in such cases is not an exact one, rather an approximate one.

Why To Use The Greedy Algorithm?

1. In many cases greedy algorithm is the most intuitive approach to solve a given optimization problem, that is, it is often the first-guessed solution and is easy to formulate.
2. Correct greedy algorithms are often more powerful and fast as compared to other approaches such as dynamic programming.

This is because the greedy approach has to consider only one locally optimal choice while moving ahead with the solution, while dynamic programming must check all possible cases. 3. Greedy algorithms work for a wide range of problems (such listed here), many of which have real-life applications in fields such as designing networking protocols and scheduling multiple events.

Architecture Of The Greedy Algorithm

The basic architecture of the implementation of any greedy algorithm is as follows:

Input to Algorithm: Function = F, Set of Inputs = C

Output: Solution Set Which Maximizes or Minimizes Function

Steps:

Here

1. Select() function makes a greedy choice from the input set C
2. isFeasable() function checks whether the choice made by Select() function leads to an optimal value of F

Properties of Greedy Algorithm

There is no defined mathematical way to check the correctness of a given greedy algorithm.

But it has been observed that many optimization problems that can be solved using some greedy algorithm satisfy 2 properties as given below:

1. Greedy choice property
2. Optimal substructure property

To understand these 2 properties in a better way, we will make use of an example problem.

The Indian Coin Change Problem If we want to make a change for $X$ rupees, and we have an infinite supply of each of the denominations in Indian currency, that is, $\{1, 2, 5, 10, 20, 50, 100, 500, 1000\}$ valued coins, what is the minimum number of coins needed to make the change?

Greedy Choice Property

• A problem is said to exhibit greedy choice property if the globally optimal solution can be reached by making locally optimal (greedy) choices. These choices are not dependent on our future choices, and can not be altered after they have been made.
• It is equivalent to showing that there is an optimal solution to the problem that is obtained by only greedy choices.

It can be seen using brute force solutions that the optimal solution for some $X$, say 76, is made up of greedy choices only as follows:

$\ce{76 ->[-50] 26->[-20] 6->[-5] 1->[-1]0}$

So the solution set comprising of the minimum number of coins required for exchange is $\{1,5,20,50\}$. As we can see, it consists of all the greedy choices, that is, choosing the coin of the largest denomination that is equal to or less than the value of the amount left.

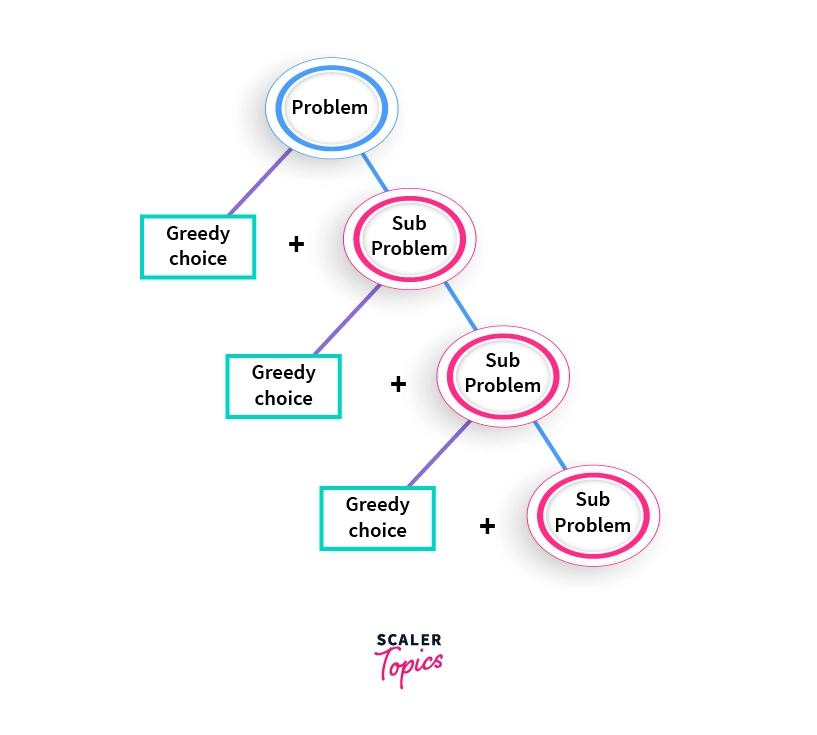
Optimal Substructure

A problem is said to exhibit optimal substructure property if the global optimal solution to the said problem can be constructed by combining the greedy choice made with optimal solutions to the subproblem of the original problem.

Schematic Diagram of Optimal Substructure

Let's break the above problem (for $X = 76$) into 2 parts:

1. The greedy choice: Choosing the largest possible coin denomination $\le$ 76, that is the coin with value 50.
2. The Subproblem: Applying our greedy algorithm on $Y = X-50 = 26$. As was seen above, the solution set for the subproblem is $\{20, 5, 1\}$.
3. Combining Solutions: Combining the greedy choice with the solution set of the subproblem, we get

$\{50\}\cup\{20, 5, 1\} = \{50, 20, 5, 1\}$

Output :

that was the globally optimal solution for $X=76$ as was shown in the above section.

Since combining the greedy choice with the subproblem's optimal solution gives us the global optimal solution to the original problem, we can say this problem exhibits optimal substructure.

Providing rigorous mathematical proof for greedy choice and optimal substructure is out of the scope of this article. Interested readers can refer this article and this article for further insights and rigorous treatment of the stated properties.

Key Terminologies used in Greedy Algorithms

Some of the key terminologies or the technical terms which are commonly associated with a greedy algorithm based solution are as follows:

1. Objective Function

This is the function whose output we require to maximize or minimize for a given set of inputs. In other words, it is the mathematical formulation of the given optimization problem.

In the example taken above, we can define our objective function as follows:

$f(m)$ = Minumum coins required to make a change of $m$ rupees

2. Candidate Set

A candidate set is a collection of items that the greedy algorithm takes as input. It can be a set of numbers, nodes of a graph, characters of a string, etc. The solution for the global optimization is a subset of the candidate set.

In the problem we described above, our candidate set is the infinite set of coins:

$C$ = $\{1.., 2.., 5.., 10.., 20.., 50.., 100.., 500.., 1000..\}$

3. Selection Function

A selection function is the one that determines the next candidate (from the candidate set) that should be chosen to build the solution.

For the above-used example, the selection function can be defined as

where the method max_element(C) returns the maximum value present in set C.

4. Feasibility Function

The feasibility function determines whether a given element can be used to build a global solution. Or in other words, whether the given candidate is feasible for optimization or not.

For the above-used example, the feasibility function can be defined as:

Here, this function checks if the coin chosen from the candidate set $C$ has a value greater than the amount left.

• If yes, then this coin cannot be used to make the change, otherwise use it.
• If the coin cannot be used, then remove it from the candidate set also.

Advantages Of Greedy Algorithm

1. All greedy algorithms are very intuitive and can be guessed easily.
2. Greedy algorithms are generally easy to understand as well as implement.
3. If correct, greedy algorithms find the optimal solution much faster as well more efficiently than its alternatives, such as dynamic programming.

Disadvantages Of Greedy Algorithm

1. Though very intuitive, it is very hard to prove mathematically the correctness of a greedy algorithm to solve the given problem at hand.
2. A greedy approach to solve optimization problems may not always be correct, may even lead to the worst possible solution (as in the case of the Travelling Salesman Problem).