Heap Data Structure

heap data structure are a special kind of tree data structure that follow the under-given conditions:

1. The given tree should be a complete binary tree.
2. It should satisfy the heap property. It means that all the children of a given node must be greater than the parent node, or all the children must be smaller than the parent node.

To better understand heaps, let us first understand what binary trees and complete binary trees are.

What are Binary Trees?

A binary tree is a tree data structure(we shall add a link to the tree article here) whose all nodes have either zero, one, or at most two children nodes. These two children are generally referred to as left and right child respectively.

The top-most node is known as the root node, while the nodes with no children are known as leaf nodes.

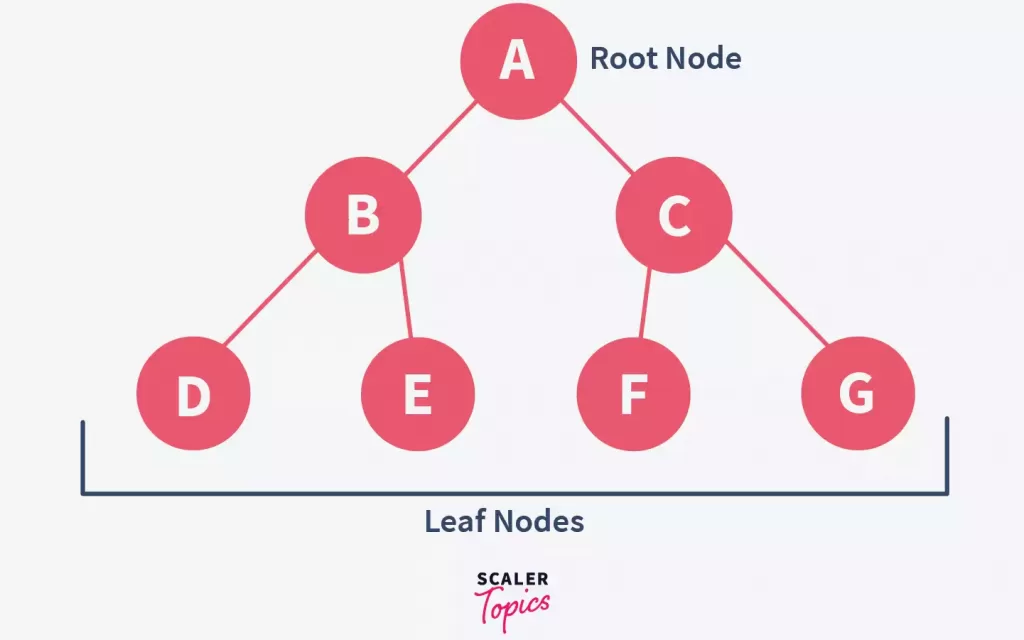
Notice how the nodes A, B & C contain at most two child nodes. Therefore, the above-given diagram represents a binary tree.

Now let us look at how to represent a binary tree through an array. It is important since it helps in understanding complete binary trees.

Array representation of binary trees –

One of the most interesting properties of a binary tree is that we can arrange all the elements of it in an array. And, the indexes of the elements in this array can be used to find the parent or children of any node.

To further explain this, consider the above-given tree. It has 7 nodes, and each node can be arranged as an element of an array –

Now, if the index of a given element is i,

1. $2i + 1$: The element at this index will give the left child of the element at i.
2. $2i + 2$: The element at this index will give the right child of the element at i.
   3.(i – 1)/2: The element at the lower bound of this index gives the parent of the element at i

Consider $i = 1$. Placing 1 in the above equations will give:

1. $2(1) + 1 = 3$. Here, it is clear that element at index 3 i.e. D is the left child of the element at index 1 i.e. B.
2. $2(1) + 2 = 4$. Here, according to the equation, the element at index 4 i.e. E is the right child of the element at index 1 i.e B.
3. (1 – 1)/2 = 0. Here, according to the equation, the element at index 0 i.e. A is the parent of the element at index 1.

Now let us understand the first condition that makes a binary tree a heap – complete binary trees.

What are Complete Binary Trees?

A complete binary tree is a binary tree in which all the elements are arranged without missing any sequence.

In a complete binary tree –

1. All the levels are completely filled except the last level that may or may not be completely filled.
2. Elements are filled from left to right.

Consider a binary tree –

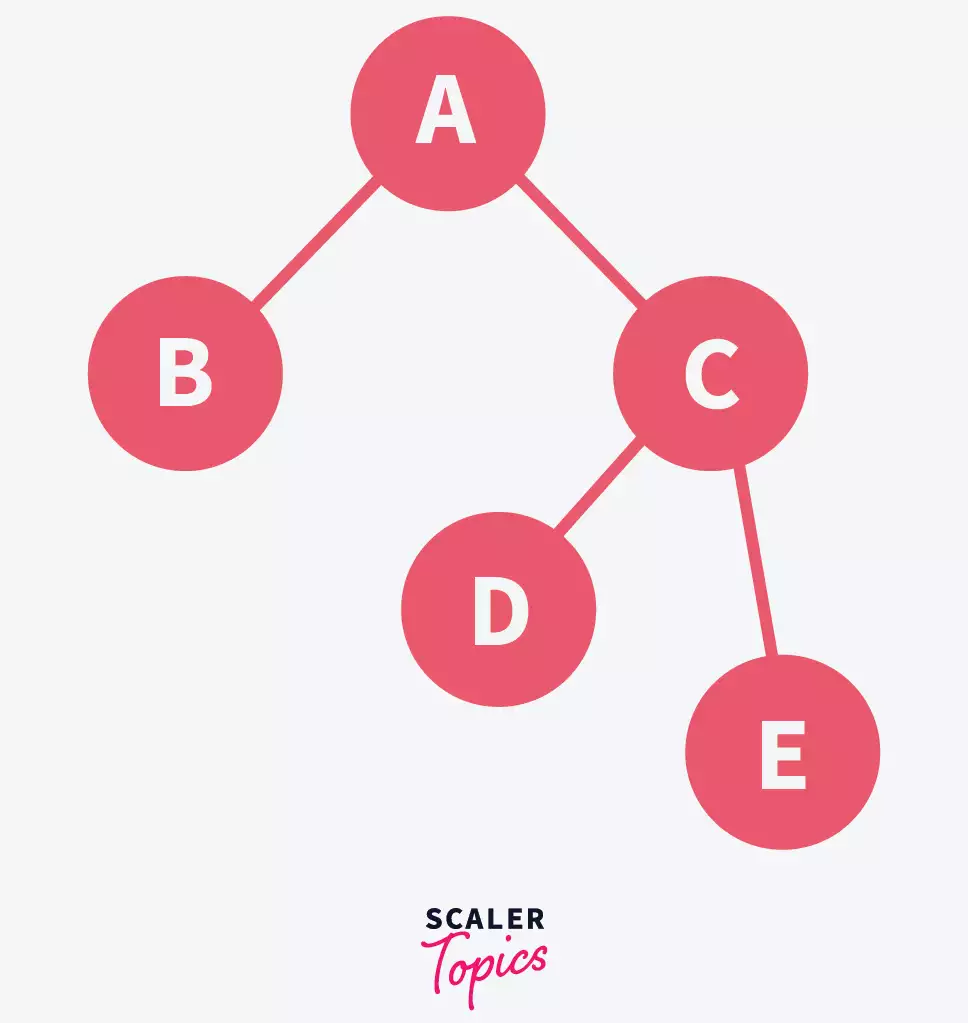
If we were to represent it as an array, we can not do the following –

Doing this will violate the equations that tell us the index of parents and children of a given node.

Notice how according to the equations, E should be the right child of B, which is not true. Thus, to preserve the equations, the array should rather be formed this way –

In the above-given diagram of the array, there are empty spaces in between the elements. Therefore, according to the definition of a complete binary tree, we can say that the above-given tree is not a complete binary tree.

The following trees are complete binary trees since they have no empty spaces in them.

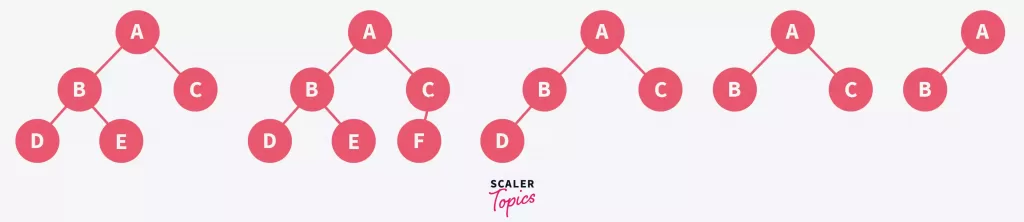
All full binary trees are complete binary trees, however, all complete binary trees are not full binary trees.

With this, we have understood the first condition for a binary tree to be called a heap. Now, let us discuss the second condition that is heap property. According to this condition, there are two types of heaps – max-heap & min-heap that are discussed below.

Types of Heap Data Structure

1. Min-heap:

If in a complete binary tree, all the nodes (including the root) are smaller than their respective child nodes, it is known as a min-heap.

In a min-heap, the root element is always the smallest of all the elements present in the heap.

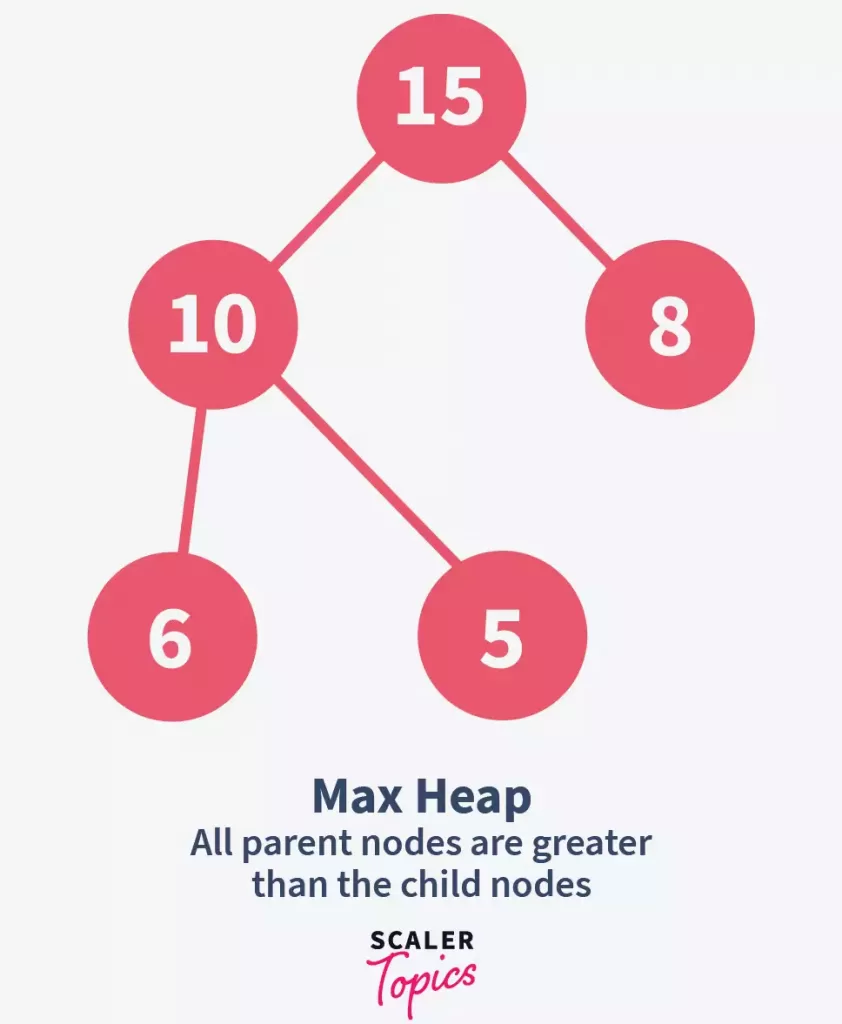
Consider the following tree. It is a complete binary tree. Notice that 5 is smaller than both of its children, 8 and 6. Same for element 8 which is smaller than its children, 10 and 15. Thus, we can say that it is a min-heap

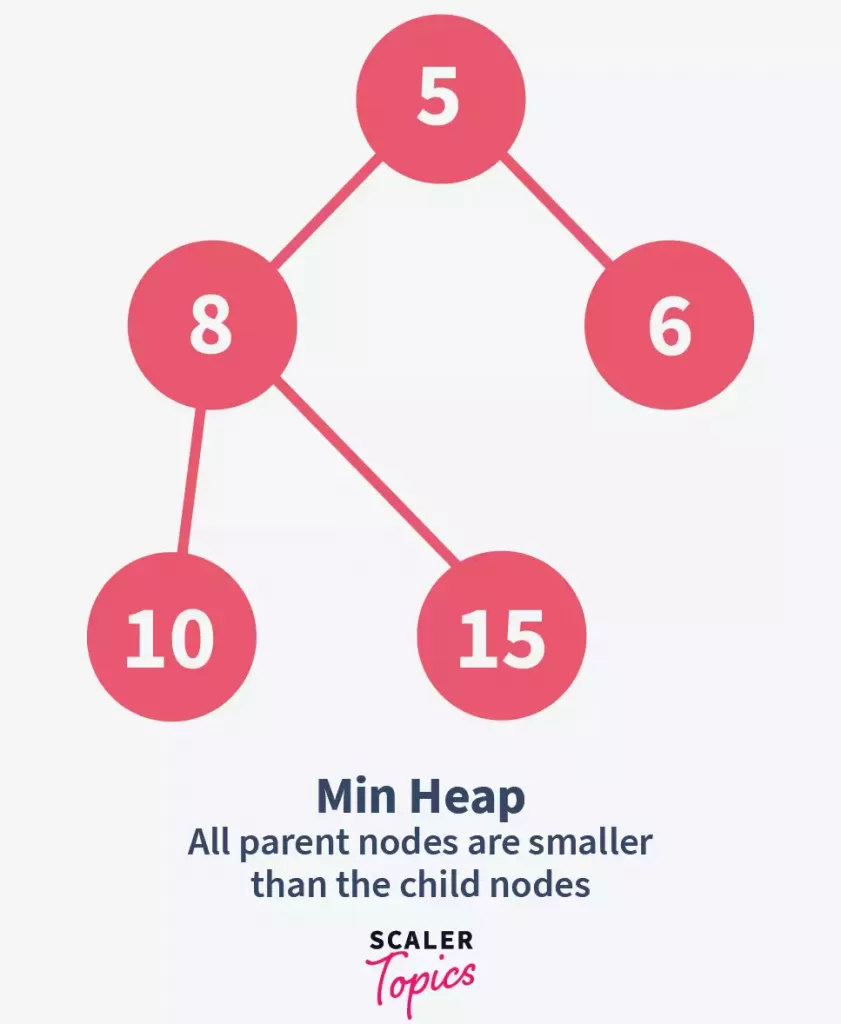
2. Max-heap

If in a complete binary tree, all the nodes (including the root) are greater than their respective child nodes, it is known as a max-heap.

In a max-heap, the root element is always the greatest of all the elements present in the heap. Consider the following tree. It is a complete binary tree. Notice that 15 is greater than both of its children, 10 and 8. Same for element 10 which is greater than its children, 6 and 5. Thus, we can say that it is a max-heap.

Now that we know what heap Data Structure are, let us understand what are the operations that can be performed over heap data structure.

Heap Data Structure Operations

Every data structure has some operations like insertion, deletion associated with them. Heaps are no different, and there are many operations that can be performed on heap data structures. We will be discussing these operations over a max-heap since the same operations can be applied to a min-heap also.

Insertion in Heap

Consider we have an array with elements 10, 8, 5, 15, 6 in it. To build a max-heap using the given elements, Follow the under-given steps –

1. Add the first element, 10 in the tree. It is the root element in the tree:

2. Add the next element in the tree. Compare it with the parent element. If it is greater than its parent element, swap their positions. It is done to ensure that the tree follows heap conditions, and a max-heap is maintained each time an element is added. Here, we should add the second element, 8 as the left child of the root element because a heap is filled from left to right. No swapping occurs here because 10 is greater than 8.

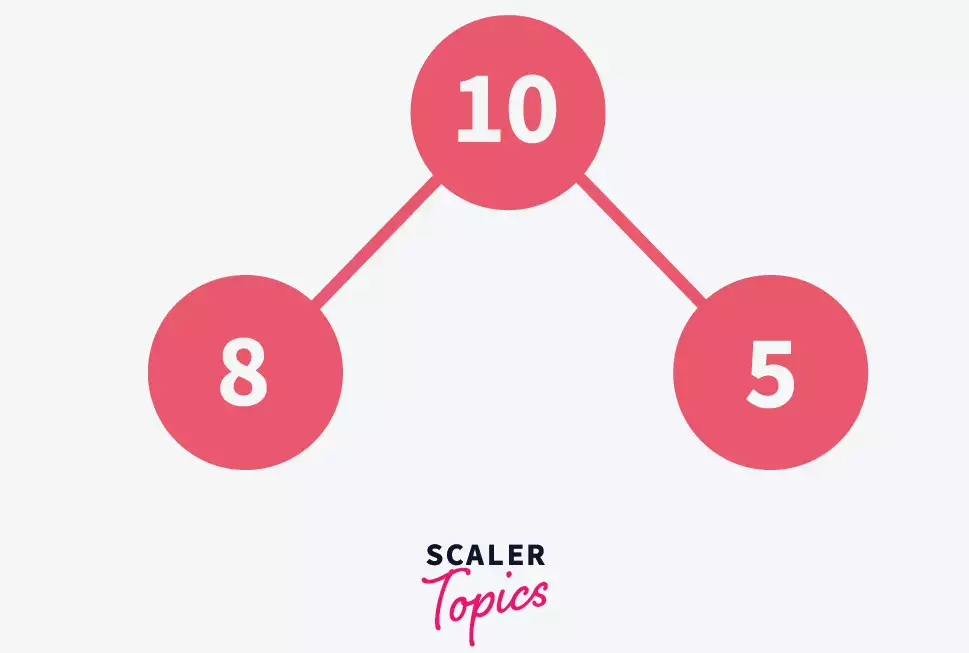
3. Repeat the above-given step with the next element, 5.

4. Add the next element, 15 in the tree.

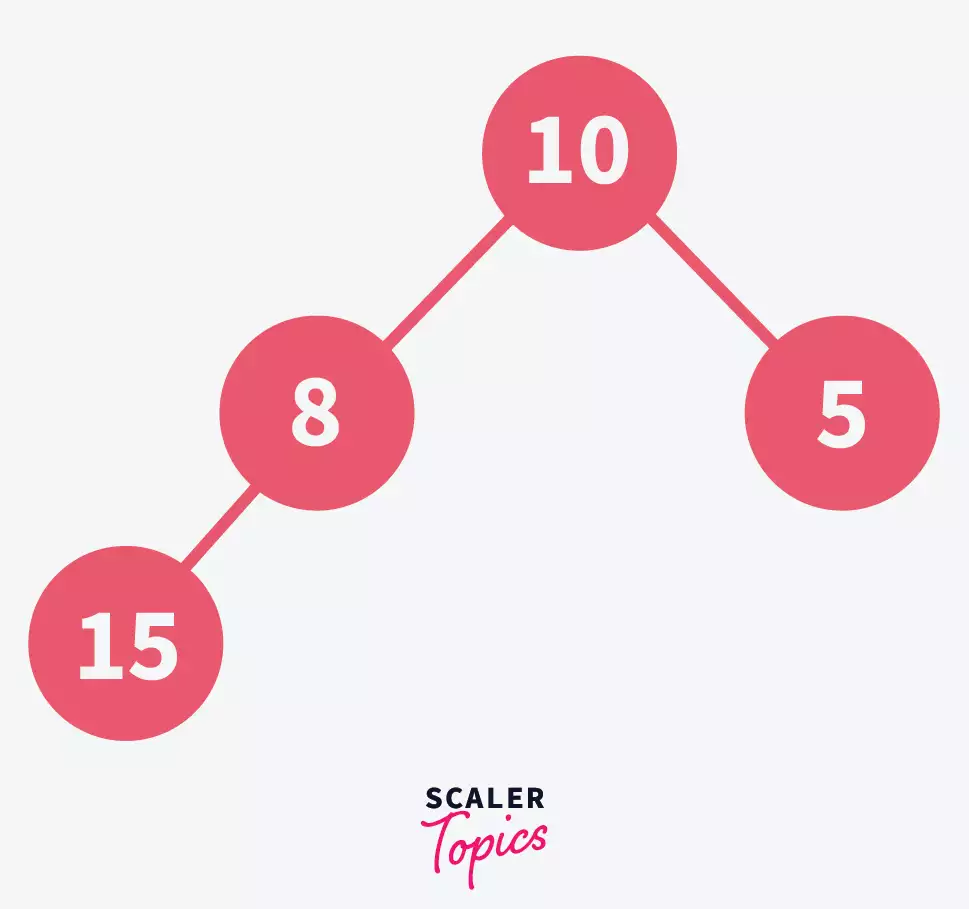
   Now since 15 is greater than its parent element 8, this tree is not a max-heap anymore. To make it a heap again, we will swap the positions of 8 and 15.

   Again the obtained tree is not a max-heap since 15 is greater than its parent element, 10. We will again swap the positions of 10 & 15.

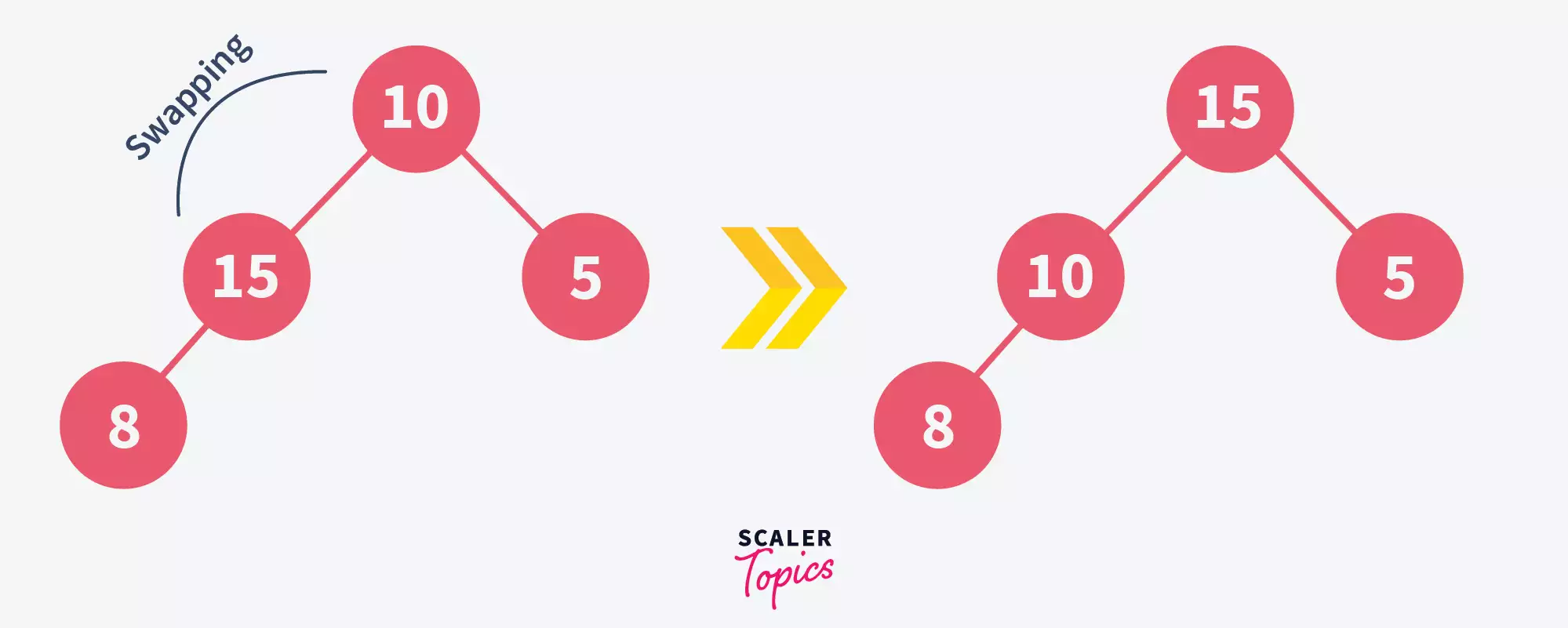
   This step is performed using recursion, and done until the inserted element finds its correct position in the heap.

   Notice that 15 was first added at the bottom of the tree and then moved up to its correct position. This moving up of elements is known as bubbling up.

5. Add the last element, 6 in the heap by comparing it with the parent.

With this, we have added all the elements of the given array into a heap.

One thing to note here is that a comparison is done each time an element is added. The number of comparisons also depends on the height of the tree. In the above case, a total of 5 comparisons were made. This results in a time complexity of O(nlogn) since the height of a binary tree is logn.

But we can reduce the number of comparisons by using a method called heapify where elements are first added into the tree and then arranged in a bottom-up fashion. It helps in reducing the number of comparisons, and thus the time complexity of the overall algorithm.

So, let us understand how to heapify a binary tree.

How to Heapify a Binary Tree?

Heapify is the process of rearranging the elements to form a tree that maintains the properties of the heap data structure.

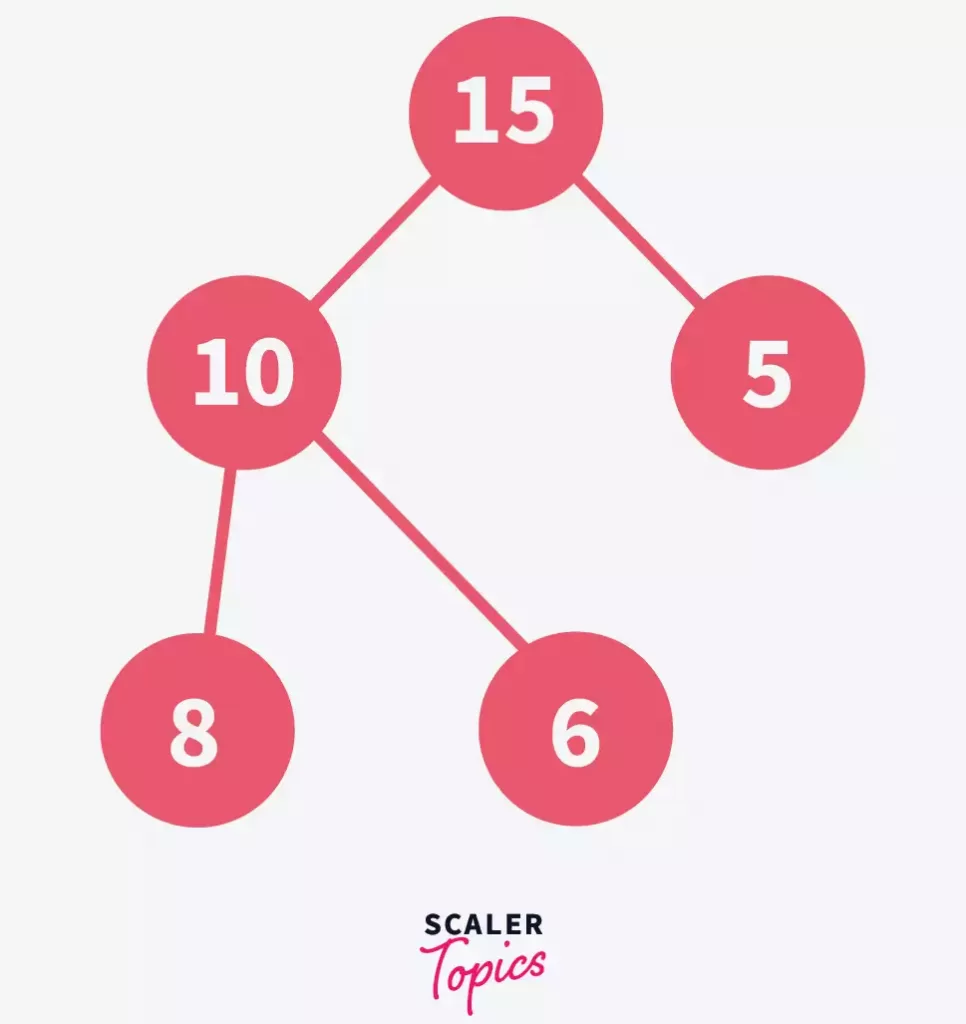
Recall the list/array that had the elements – 10, 8, 5, 15, 6 in it. To heapify these elements, and form a max-heap, let us follow the under-given steps –

1. Visualize all the elements of the list as a complete binary tree –

   Treat the elements of the given array as the nodes of a tree. To visualize an array as a binary tree, refer to the part where we have discussed the array representation of the binary tree.

   

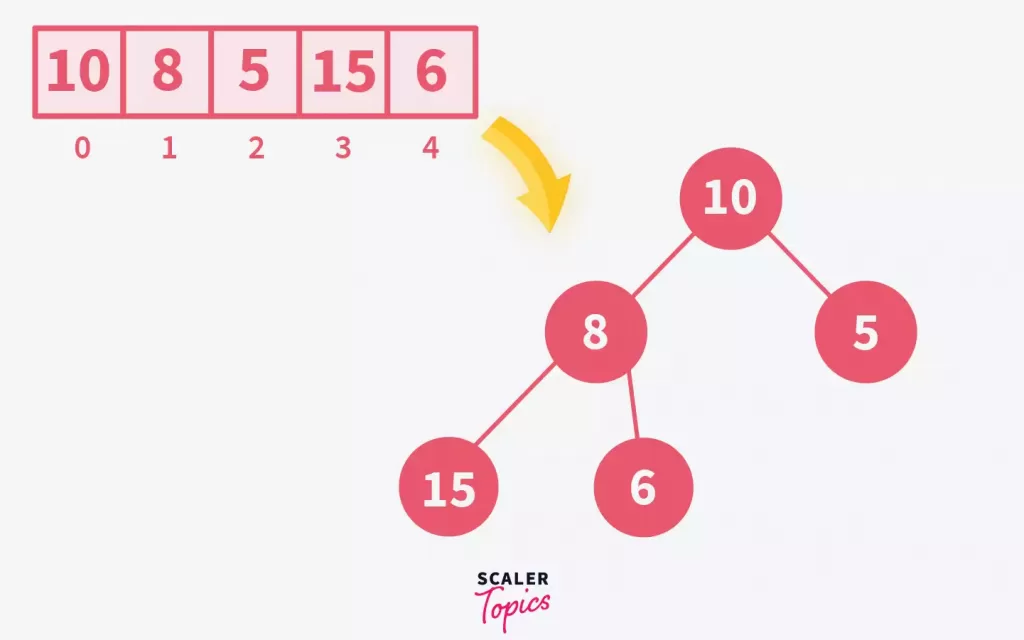
   Notice how the above-given binary tree is a complete binary tree but does not satisfy the properties of a max-heap since element 8 has an element greater than itself as its child.

2. Start from comparing the values of children nodes with that of the parent. If the value of the parent is smaller than the values of the children, swap it. Swapping is done with a larger of two children. This process is repeated until every node satisfy the properties of a max-heap –

   Here, we start comparing 8 with 15 and 6. Now, since 15 is greater than 8, we will swap their positions.

   

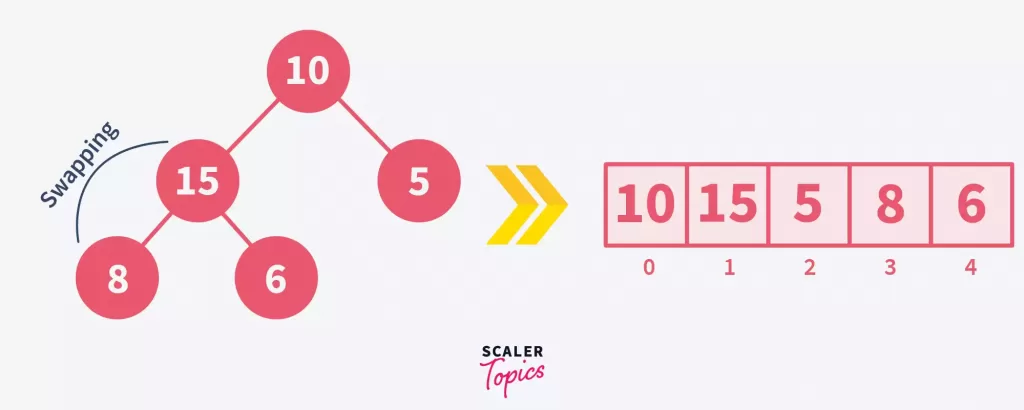
   Again, the property of max-heap is not satisfied since 15 is greater than 10. Therefore, we will once again perform the above step.

Now that we have obtained a max-heap, we can stop this step.

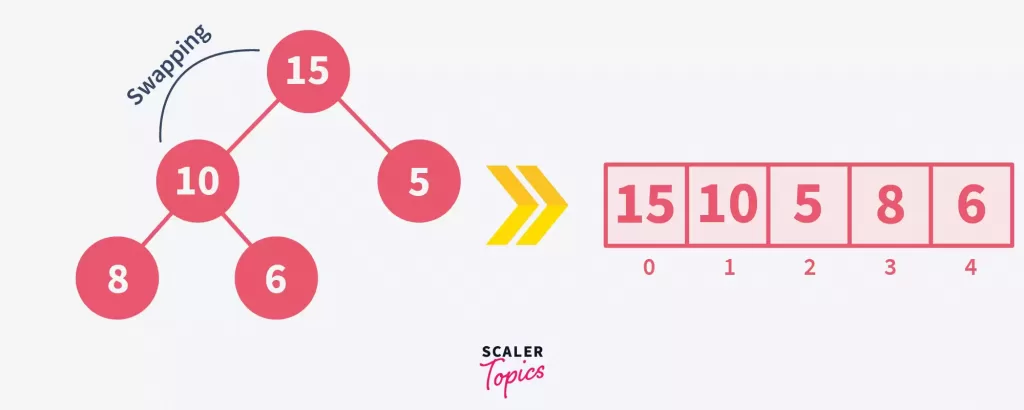
One interesting thing to note here is that a node can be heapified iff all the children nodes are already heapified. This is the reason why we start from the bottom-most sub-tree.

This step is also performed using recursion. We create a function called heapify() that works by dividing the tree into smaller sub-trees and then comparing the values of parents with that of children in each sub-tree.

Notice that the number of comparisons are reduced slightly. This way, we can significantly reduce the comparisons if there are many elements to be added.

Here, the time complexity would be equal to the height of tree O(logn). This is because a node will be compared only to its parent, and thus, will be swapped at most O(logn) times.

Now let’s understand how to delete elements from a heap.

Deletion from Heap

Let us consider the following max-heap that we created in the last step-

To delete the elements from a heap, we follow the under-given steps –

1. Search for the element to be deleted and swap it with the last element in the heap, let’s say we want to delete 10-

   

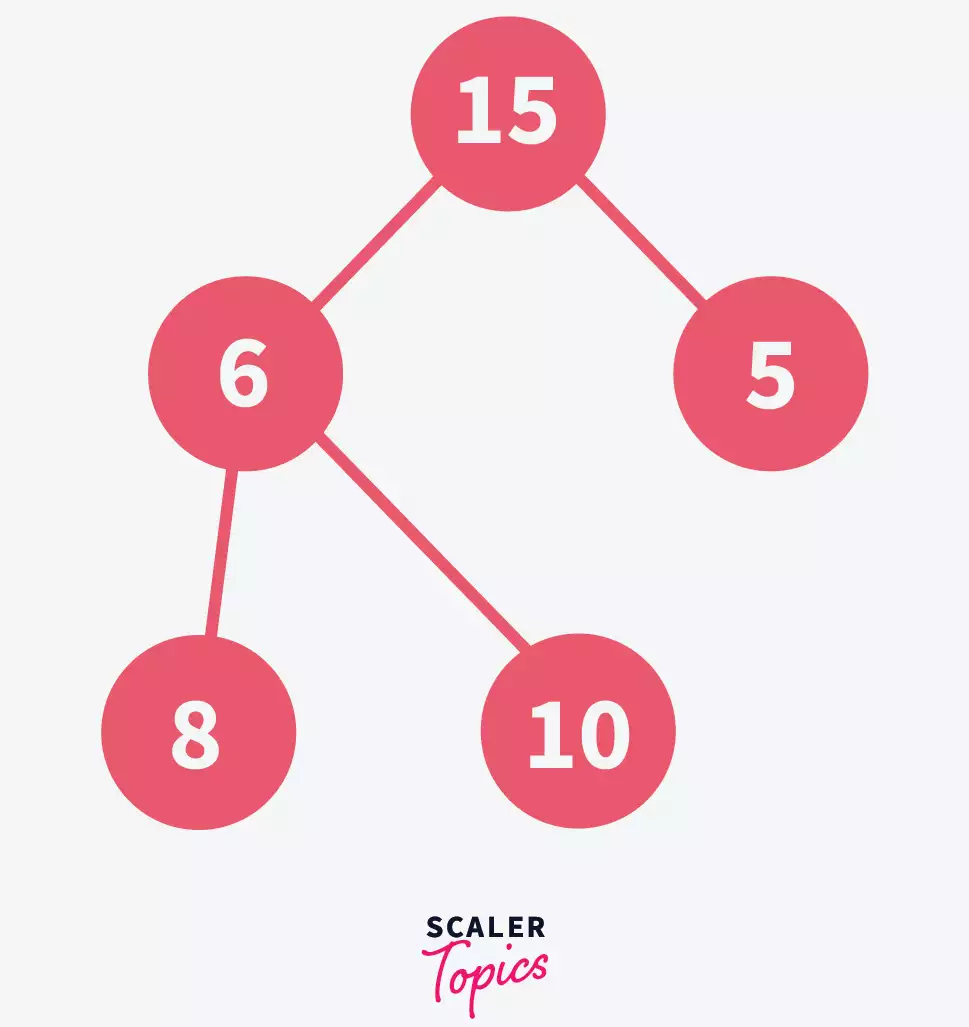
   Here, we have swapped the position of 10 with the last element that is 6

2. Remove the element from the tree –

   

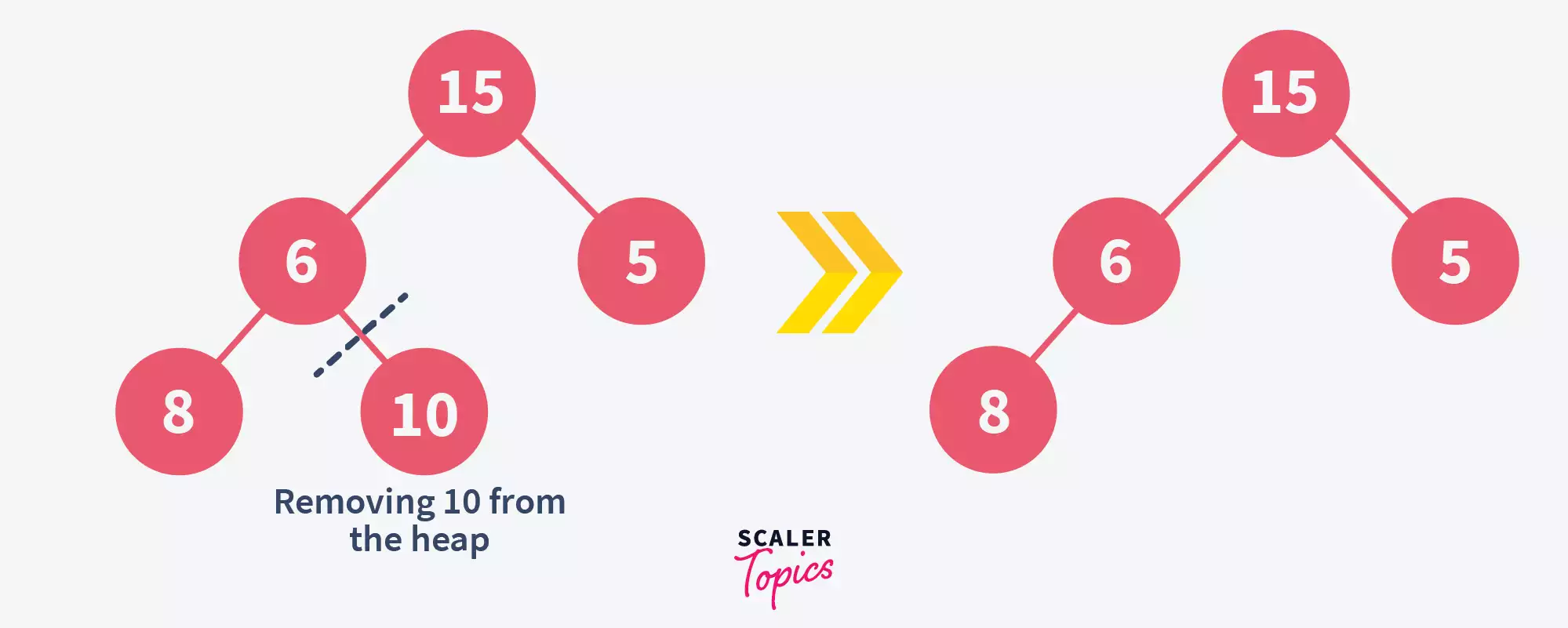
   But now, the remaining heap is not a max-heap anymore. So, as the next step, we should heapify it once again.

3. Heapify the tree again-

   

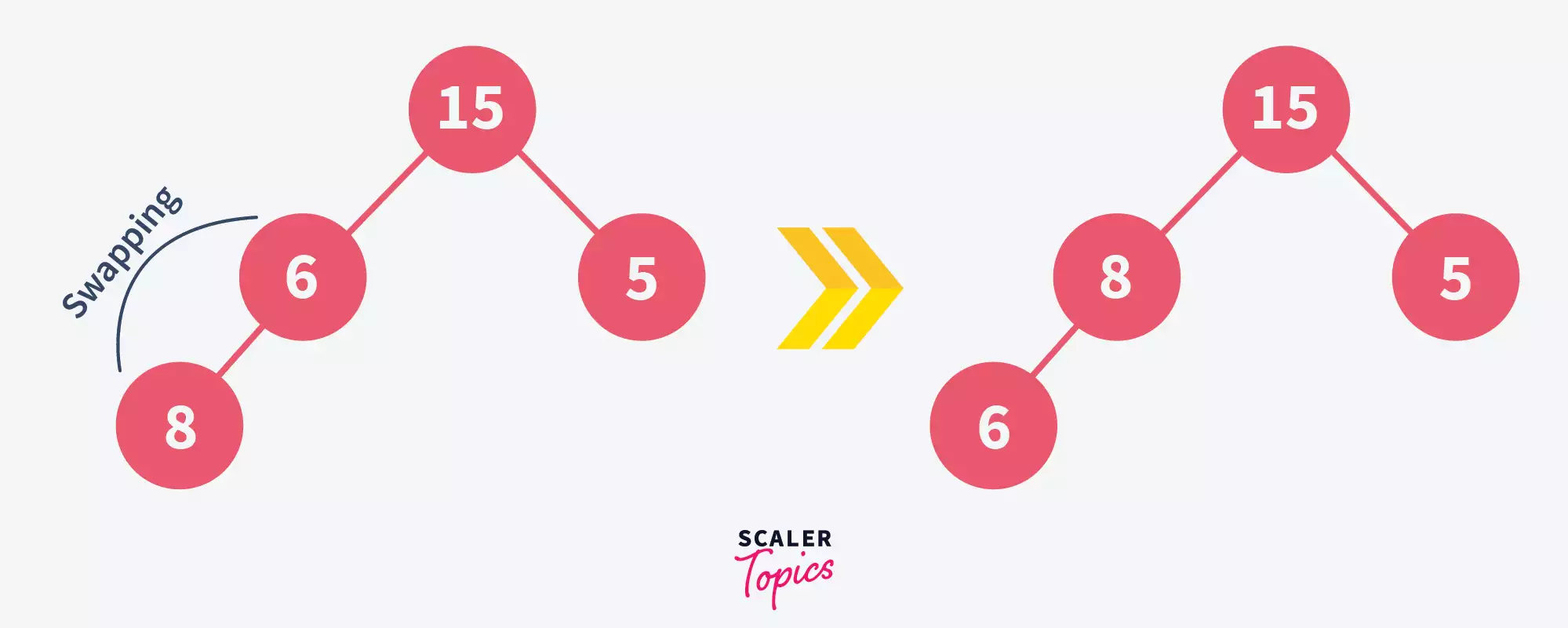
   Here, we have once again heapified the given tree to form a max-heap.

Thus, we have successfully removed 10 from the heap.

Now let us write some code to implement a max heap.

Implementation of Heap

1. C

2. C++

3. Python

• Heap in Python