Linear Search Algorithm

Introduction to Searching Algorithms

This is the first part of a three-part series on Searching Algorithms.

Searching is one of the most commonly used programming concepts in everyday life. Whether you’re shopping on Amazon, Googling on Google, or finding the next thing to binge on Netflix, it’s all around us. If you think about it, you have landed on this article today by Googling on Google only, or maybe Bing 😛

In computer programming, searching is usually referred to as finding a particular element in a data structure. For example, let’s say we want to find the word “Scaler” in the following sentence –

I like Scaler Academy very much

As we can see, Scaler is the third word in the above sentence. That’s easy when you’re looking with a naked eye and the data set is so small.

But if someone asks you to find a word in a document containing hundreds and thousands of words and sentences, it’ll be not so easy right?

That’s exactly what we’ll learn today; how to write a program to find an element in a data set.

Types of searching algorithms

If you’re searching for a product on Amazon, and it takes minutes for the search result to pop up, you probably won’t be a very satisfied customer. That is why efficient searching is one of the most important components of user experience.

Hence, it is important to understand different searching algorithms and why it is important to use one over other. Below are some of the most commonly used ones.

• Linear Search

• Binary Search

• Interpolation Search.

Today, we’ll be talking primarily about Linear Search. You can refer to more articles as well on Scaler where we deep dive into other search algorithms.

A little heads up, all code snippets below are in Java 8.

What is Linear Search?

Linear search is a simple searching algorithm that sequentially checks each element in a list or array until it finds the desired value or reaches the end of the list. It starts at the beginning and compares each element with the target value until a match is found or the entire list has been traversed. If the target value is found, the linear search returns the index of the matching element. If the target value is not present in the list, the search returns a special value, such as -1, to indicate that the value was not found. Linear search has a time complexity of O(N), where N is the number of elements in the list or array being searched.

How Linear Search Works?

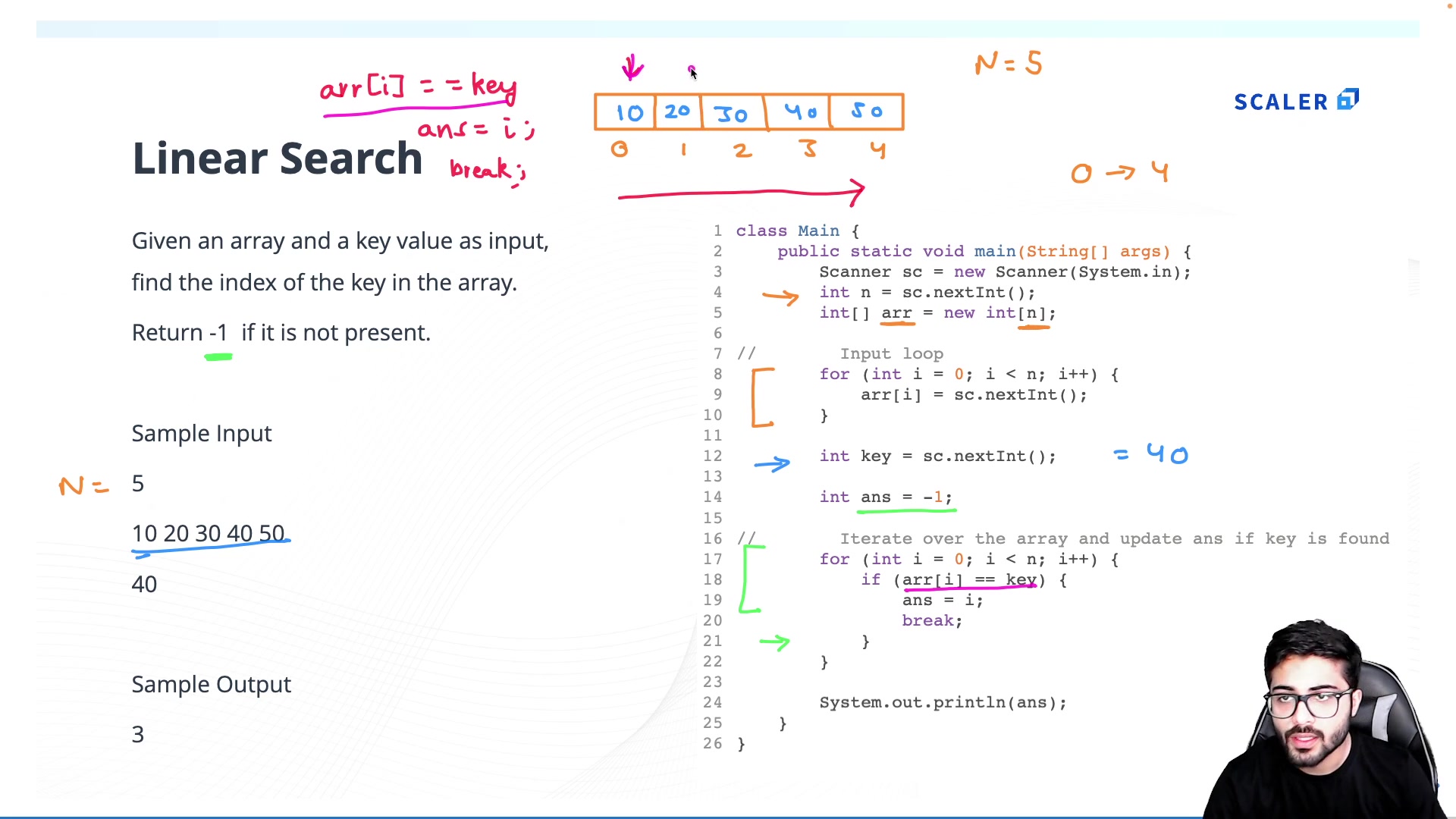
Let’s say we’re trying to search for a number, K, in an array containing random integers.

Let’s say the array is

5 3 12 9 45 1 22

And the element we’re searching for, K = 9

What is the most intuitive way to do it?

If you’re thinking to start from the beginning of the array, and check whether the element is equal to K or not, until you either find K or reach the end, congratulations you’ve just defined Linear Search yourself 😛

Let’s define it more clearly.

In Linear search, we traverse each element of the array, one by one, and check whether it is equal to the element to be searched. It is also called sequential search because it checks all the elements sequentially.

If you find an element equal to K, we can say that K is present in the array. If we reach the end and still haven’t found K, we can confirm that K is not present in the array. Let’s try to use linear search for the above input.

5 3 12 9 45 1 22 – Found K = 9 at index 3

As you can see, we found K in the fourth comparison.

You can argue that why do we need to start from the beginning, and not the end or the middle. You’re right, we can do either of those. But think about it, does it really help? The answer is: not really.

If you try to search for 9 from the end rather than the beginning, you’ll find it in the fourth iteration only.

5 3 12 9 45 1 22 – Found K = 9 at index 3

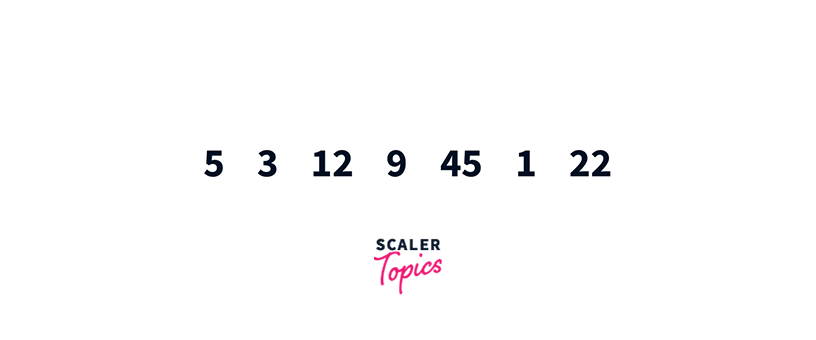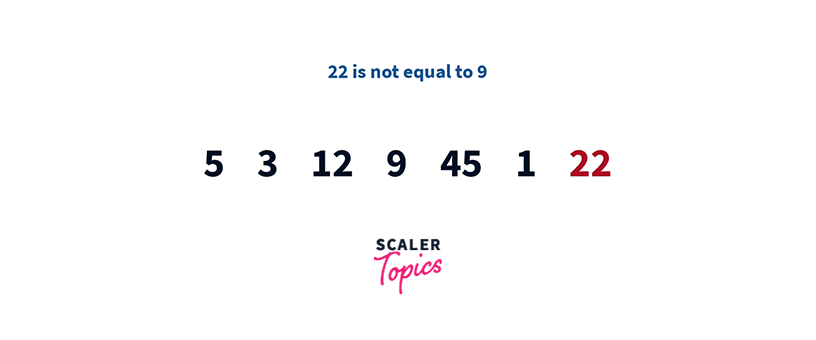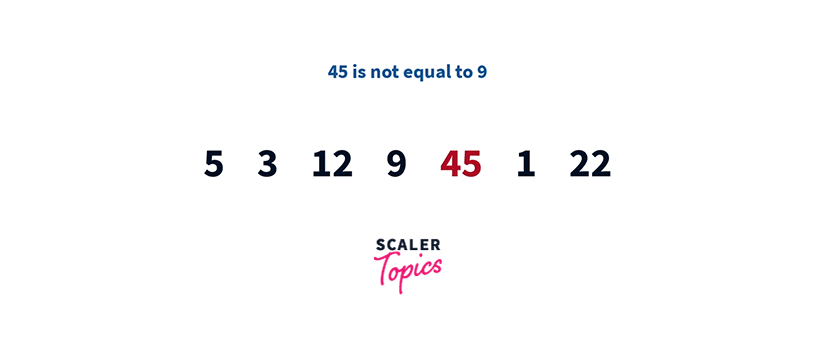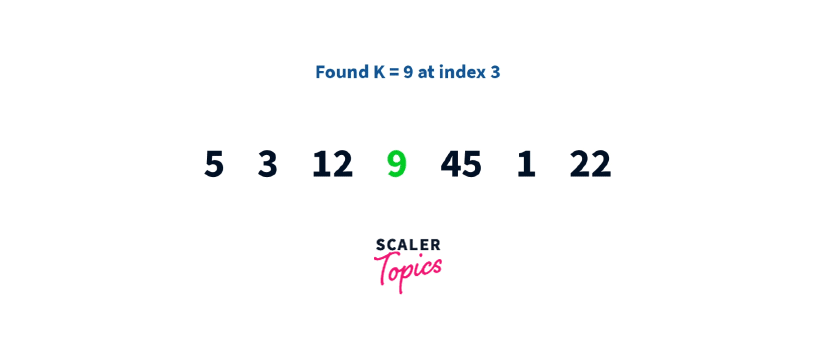
To simplify, if K is present in the first half of the array, it’ll be better to start from the beginning. On the other hand, if it’s present in the latter half, it’s better to start from the end.

But think about it; in the case of a completely randomised array, do we really know where the element might be present? Or even the fact that whether it is present or not? We don’t, right? That’s what we’re using linear search for.

In fact, it is quite possible that if you start from the beginning, K might be the last element of the array and if you start from the end, it might be the first one.

So if we consider the worst case possibility, every time we will end up searching the complete array only. Hence, it hardly matters where we start the search from.

Algorithm for Linear Search

Below is the algorithm for Linear Search.

1. Initialise i = 0 and n = size of array
2. if i >= n, which means we have reached the end of the array and we could not find K. We return -1 to signify that the element K was not found.
3. if arr [ i ] == K, it means that we have found an element that is equal to K at index 'i’ and we do not need to search the remaining array. We return the index 'i’ directly from here which is the index at which K was found in this array
4. else arr [ i ] != K, which means the current element is not equal to K and we will repeat step 2 with the next element of the array by incrementing i, i.e. ++i

Implementation of Linear Search Algorithm

Below is a simple implementation of Linear Search in Java.

Output:

Time Complexity of Linear Search Algorithm

In the best case, we might find K in the first iteration only, i.e. it is the first element of the array.

In the worst case, we might find K in the last iteration or not find K in the array at all.

On average, it might be present somewhere around the middle of the array.

So, we can probably conclude that the average case time complexity of the linear search is O(n/2) ~ O(n), where n is the number of elements in the array. Hence, the time complexity of the linear search is in fact, linear 😛

Space Complexity

As it is evident, we are not using any significant extra memory in linear search. So the space complexity is constant, i.e. O(1).

P.S. The variables used for iterating the array and other minor information are constant since they don’t depend on the input size of the array.

Applications of Linear Search Algorithm

Linear search is the most straightforward and easiest algorithm to implement and understand. It is particularly useful if the data set is small, randomised and there are memory constraints, since it always uses constant memory.

If multiple elements need to be searched in a data set, linear search is not the most efficient approach as it will take linear time in each case on average.

Improving Linear Search

To improve the performance of linear search, you can consider the following techniques:

• Transposition: After finding the target element in the list, you can swap it with the element at the previous position. This allows for faster access to the recently searched element in future searches.

• Move-to-Front: Similar to transposition, after finding the target element, you can move it to the front of the list. This ensures that frequently searched elements are placed at the beginning, reducing the average search time in subsequent searches.

• Sentinel Search: Instead of checking for the target value at each iteration, you can introduce a sentinel value at the end of the list that matches the target value. This eliminates the need for a separate check within the loop, potentially reducing the number of comparisons.

• Sorted List: If the list is sorted in ascending or descending order, you can employ techniques like binary search to perform faster searches. This reduces the search time to logarithmic complexity (O(log N)).

• Hashing: Utilize a hash table or other hashing techniques to store the elements of the list. This allows for constant-time access to elements, significantly improving search performance.

When to use Linear Search?

Linear search is suitable in the following scenarios:

• Small Data Sets: Linear search works well with small data sets where the number of elements is relatively low. In such cases, the overhead of implementing more complex search algorithms may not be justified.

• Unsorted Data: Linear search is effective when the data is unsorted or the order of elements is not important. It sequentially checks each element until a match is found, regardless of the arrangement of elements.

• Singly Linked Lists: Linear search is commonly used in singly linked lists where direct access to elements is not possible. It traverses the list one node at a time, making it a suitable choice for searching through linked structures.

• Infrequent Searches: If searches are infrequent or the list is not frequently updated, linear search can be a straightforward and sufficient solution. It requires minimal setup and is easy to implement.

• Educational Purposes: Linear search is often used as an introductory algorithm in programming and computer science courses to illustrate basic search concepts before moving on to more advanced algorithms.