Introduction

Before jumping onto what is load factor and Rehashing, I would suggest learning more about hashing and collision. Pre-requisites:

• Hashing

In short, whenever we need to insert some Key-Value(e.g. Key= Roll Number and Value= Student Details), and since we have limited space available in any Data Structures, we basically use the concept of hashing the Key to get an Index inside the Array where we can store this Key-Value.

E.g. If Student = {Roll No=1000, name=Anmol, Age=25, Address=New Delhi} And say the array has a size of e.g. 50(total 50 students are there in the class).

Then we hash the Roll Number = 1000, to get some value <= 50, and place this at that Index.

E.g. The easiest hash function is modulus i.e. we take key % arrSize = 1000 % 50 to get 0.
So the Student with Roll Number 1000 can be placed at index 0 of the array of size 50.

But if we notice carefully, we can observe that for 2 such keys we can get the same Index, e.g. the above hash function(of modulus) will give 0 for Key=1000 and 1050.
So in that case we need to place both Students will Roll numbers = 1000 and 1050 at Index 0. And such a scenario is called Collision.

There are several Collision resolution techniques discussed in the above-linked article, but in this article, we will focus on Rehashing, which is a collision resolution mechanism, and on Load Factor which represents how much load is there on such a data structure where the Key-Values are stored.

By load we mean with increasing more and more inputs(key-values) to store, at some point of time we might run out of space, and the collision chances would increase drastically. Since the goal is to keep Collision to almost zero, the Load-Factor decides when we should increase the size of this data structure. We will look into them in more detail in the following sections.

What is Load Factor in Hashing?

As discussed above briefly, every data structure has a fixed size. The Hash table provides Constant time complexity of insertion and searching, provided the hash function is able to distribute the input load evenly.

That’s because if each element is at a different index, then we can directly calculate the hash and locate it at that index, but in case of Collision, the time complexity can go up to O(N) in the worst case, as might need to transverse over other elements comparing against the element we need to search.

So long story cut short – Hash Table should store elements with as little collision as possible.

But even with the best possible Hash function and with more and more elements coming to be stored inside this Hash table?
Then eventually we will run out of vacant indexes and will result in unavoidable collisions.
To handle such a scenario we have the Load Factor in hashing which is basically a measure that decides when exactly to increase the size of the Hash Table to maintain the same time complexity of O(1).

Let’s understand with an example with HashTable of size=16:

1. If there are 16 elements in the HashTable, the hash function method will distribute one element in each Index. The searching for any item, in this case, will take the only lookup.
2. If there are 32 elements in the HashTable, the hash function method will distribute two elements in each Index. The searching for any item, in this case, will take the maximum of two lookups.
3. Similarly, if there are 128 elements in HashTable, the hash function method will distribute eight elements in each Index. The searching for any item, in this case, will take the maximum eight lookups.

So we can see more of the elements to store in that fixed space, less the search efficiency will be.

Load factor is defined as (m/n) where n is the total size of the hash table and m is the preferred number of entries that can be inserted before an increment in the size of the underlying data structure is required.

So each Data structure(like Hash table) comes with 2 important properties:

• Initial Capacity

The initial capacity is the number of Indexes allocated in the HashTable. It is created when the HashTable is initialized.
The capacity of the HashTable is doubled each time it reaches the threshold.
If you recall, Chaining was one of the ways of collision resolution techniques, and HashTables usually use Chaining technique. So in case the same Index is generated for multiple keys, all these elements will be stored against the same index in the form of the chain. So we can see that one Index can store multiple elements, and for the same reason this chain of elements is also referred to as “buckets”.
Buckets are the group(or chain) of elements, whose hash indexes generated from the hash function are the same.

E.g. if we have initialized the HashTable with initial capacity of 16, then the hash function will make sure the key-value pairs will be distributed among 16 indexes equally, thus each bucket will carry as few elements as possible.

• Load Factor in Hashing

The Load factor is a measure that decides when to increase the HashTable capacity to maintain the search and insert operation complexity of O(1).
The default load factor of HashMap used in java, for instance, is 0.75f (75% of the map size).
That means if we have a HashTable with an array size of 100, then whenever we have 75 elements stored, we will increase the size of the array to double of its previous size i.e. to 200 now, in this case.

How is the Load Factor Used?

The Load Factor decides “when to increase the size of the hash Table.”
The load factor can be decided using the following formula:

Initial capacity of the HashTable * Load factor of the HashTable

E.g. If The initial capacity of HashTable is = 16
And the load factor of HashTable = 0.75

According to the formula as mentioned above: 16 * 0.75 = 12

It represents that the 12th key-value pair of a HashTable will keep its size to 16.
As soon as the 13th element (key-value pair) will come into the HashTable, it will increase its size from 16 buckets to 16 * 2 = 32 buckets.

Another way to calculate size:
When the current load factor becomes equal to the defined load factor i.e. 0.75, hashmap increases its capacity.

Where:
m – is the number of entries in a HashTable
n – is the total size of HashTable

Example of Load Factor in Hashing

Let’s understand the load factor through an example.

If we have the initial capacity of HashTable = 16.

We insert the first element, now check if we need to increase the size of the HashTable capacity or not.

It can be determined by the formula:

Size of hashmap (m) / number of buckets (n)

In this case, the size of the hashmap is 1, and the bucket size is 16. So, 1/16=0.0625. Now compare this value with the default load factor.

                0.0625<0.75

So, no need to increase the hashmap size.

We do not need to increase the size of hashmap up to 12th element, because

                12/16=0.75

As soon as we insert the 13th element in the hashmap, the size of hashmap is increased because:

                13/16=0.8125

Which is greater than the default hashmap size.

                0.8125>0.75

Now we need to increase the hashmap size

What is Rehashing?

As the name suggests, rehashing means hashing again. Basically, when the load factor increases to more than its pre-defined value (e.g. 0.75 as taken in above examples), the Time Complexity for search and insert increases.

So to overcome this, the size of the array is increased(usually doubled) and all the values are hashed again and stored in the new double sized array to maintain a low load factor and low complexity.

This means if we had Array of size 100 earlier, and once we have stored 75 elements into it(given it has Load Factor=75), then when we need to store the 76th element, we double its size to 200.

But that comes with a price:

With the new size the Hash function can change, which means all the 75 elements we had stored earlier, would now with this new hash Function might yield different Index to place them, so basically we rehash all those stored elements with the new Hash Function and place them at new Indexes of newly resized bigger HashTable.

It is explained below with an example :

Why Rehashing?

Rehashing is done because whenever key-value pairs are inserted into the map, the load factor increases, which implies that the time complexity also increases as explained above. This might not give the required time complexity of O(1). Hence, rehash must be done, increasing the size of the bucketArray so as to reduce the load factor and the time complexity.

Lets try to understand the above with an example:
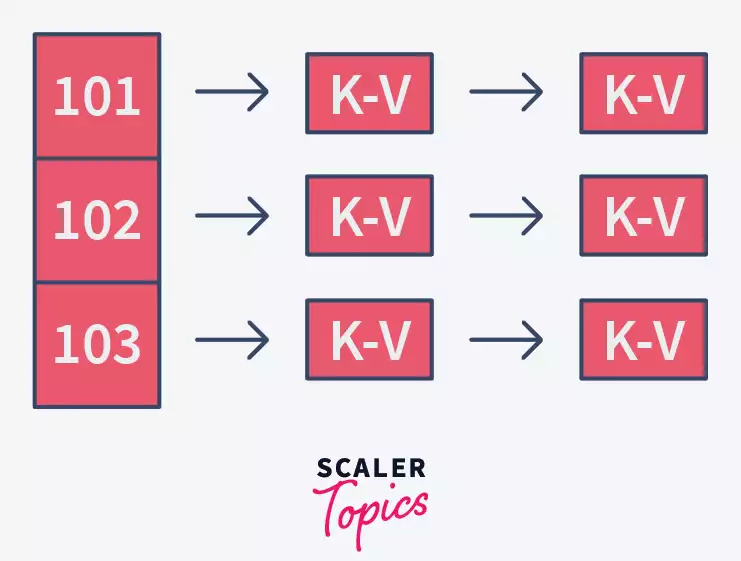
Say we had HashTable with Initial Capacity of 4.
We need to insert 4 Keys: 100, 101, 102, 103

And say the Hash function used was division method: Key % ArraySize

So Hash(100) = 1, so Element2 stored at 1st Index.
So Hash(101) = 2, so Element3 stored at 2nd Index.
So Hash(102) = 0, so Element1 stored at 3rd Index.

With the insertion of 3 elements, the load on Hash Table = ¾ = 0.74

So we can add this 4th element to this Hash table, and we need to increase its size to 6 now.

But after the size is increased, the hash of existing elements may/not still be the same.

E.g. The earlier hash function was Key%3 and now it is Key%6.
If the hash used to insert is different from the hash we would calculate now, then we can not search the Element.
E.g. 100 was inserted at Index 1, but when we need to search it back in this new Hash Table of size=6, we will calculate its hash = 100%6 = 4

But 100 is not on the 4th Index, but instead at the 1st Index.

So we need the rehashing technique, which rehashes all the elements already stored using the new Hash Function.

How Rehashing is Done?

Lets try to understand this with continuing the above example.

Element1: Hash(100) = 100%6 = 4, so Element1 will be rehashed and will be stored at 5th Index in this newly resized HashTable, instead of 1st Index as on previous HashTable.

Element2: Hash(101) = 101%6 = 5, so Element2 will be rehashed and will be stored at 6th Index in this newly resized HashTable, instead of 2nd Index as on previous HashTable.

Element3: Hash(102) = 102%6 = 6, so Element3 will be rehashed and will be stored at 4th Index in this newly resized HashTable, instead of 3rd Index as on previous HashTable.

Since the Load Balance now is 3/6 = 0.5, we can still insert the 4th element now.

Element4: Hash(103) = 103%6 = 1, so Element4 will be stored at 1st Index in this newly resized HashTable.

Rehashing Steps –

1. For each addition of a new entry to the map, check the current load factor.
2. If it’s greater than its pre-defined value, then Rehash.
3. For Rehash, make a new array of double the previous size and make it the new bucket array.
4. Then traverse to each element in the old bucketArray and insert them back so as to insert it into the new larger bucket array.

However, it must be noted that if you are going to store a really large number of elements in the HashTable then it is always good to create a HashTable with sufficient capacity upfront as this is more efficient than letting it perform automatic rehashing.

Program to Implement Rehashing

The rehashing method is implemented specifically inside rehash(), where we pick the existing buckets, calculate their new hash and place them inside new indices of the newly resized array.

Running this with the insertion and printing of 5 Key-values will output:

As we can see from the above,

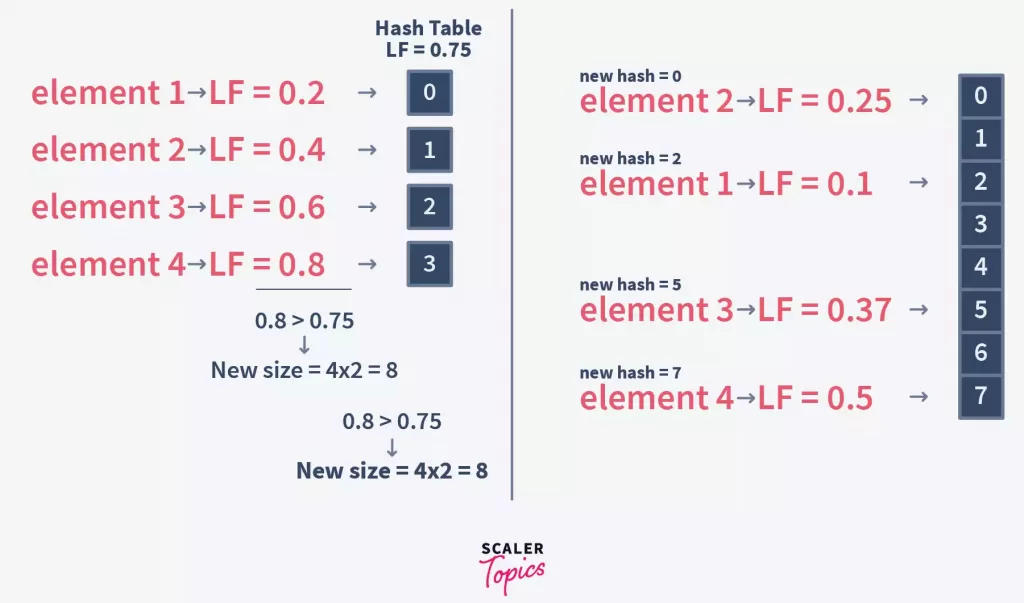
Initialcapacity = 5
Load Factor = 0.75

Element1 added, LoadFactor = 0.2, and as 0.2 < 0.75, so no need to rehash.
Element2 added, LoadFactor = 0.4, and as 0.4 < 0.75, so no need to rehash.
Element3 added, LoadFactor = 0.6, and as 0.6 < 0.75, so no need to rehash.
Element4 will have LoadFactor = 0.8, and as 0.8 > 0.75, the HashTable is rehashed.

BucketSize is doubled, and all existing elements are picked and their new hash is created and placed at new Index in newly resized Hash Table.

New size = 5 * 2 = 10.

Element4 added, LoadFactor = 0.4, after rehashing.
Element5 added, LoadFactor = 0.5, and as 0.5 < 0.75, so no need to rehash.