Radix Sort Algorithm in Data Structure

Introduction

In our previous articles, we had discussed comparison based sorting algorithms (Merge Sort, Quick Sort) which can sort the arrays in ascending/descending order in $\Omega(n\log(n))$ time $i.e.$ we can not achieve anything better than it. Then we have also seen the Counting Sort algorithm which can sort an array in linear time when the elements of the array are in the range $[0, k]$. It is a non-comparison based sorting algorithm, which operates by counting the frequency of elements appearing in the array and then arranging them accordingly.

Now let's assume we want to sort an array of length $n$ in which elements are in the range of $[0, n^3]$. In such cases, we can't use counting sort as it will take more time than comparison based sorting algorithms instead we will introduce a new sorting algorithm $i.e.$ Radix Sort

Definition of Radix Sort

Radix sort is an algorithm that uses counting sort as a subroutine to sort an array of integers/strings in either ascending or descending order.

The main idea of radix sort revolves around applying counting sort digit by digit on the given array.

Let us have a look at the formal algorithm for a better understanding

Radix Sort Algorithm

In counting sort, we have seen that we can sort an array based on the frequency of elements in the array. But the only difficulty there was if the range of elements is very large then it's not efficient to use counting sort.

So we have come up with the Radix sort where we apply counting sort digit by digit from least-significant digit to most-significant digit.

Radix sort is a stable sorting method that uses counting sort as a subroutine. It is recommended to use radix sort on positive numbers only, however with some modification to standard radix sort algorithm we can also sort an array containing negative elements.

Steps Involved in Radix sort to sort an array in ascending order are --

• Find the maximum element of the array, let it be $max$
• Find the number of digits in $max$, let it be $k$.
• For each, $i$ ranging from $1$ To $k$, apply the counting sort algorithm for the $i^{th}$ least-significant digit of each element. If any element has less than $i$ digits consider $0$ at its place (Because $29$ can also be represented as $029$).

Using this method you can also sort numbers that fit in 32/64-bit data types (int, float, double, etc) which was practically not possible with counting sort algorithm.

Note - If you haven't gone through Counting Sort yet, please have an eye on it once as it is a prerequisite for Radix Sort and if you want to sort an array in descending order, then tweak the counting sort function such that it sorts array in reverse order.

Example of Radix Sort Algorithm

Let's assume we have an array $a=[682, 244, 73, 6, 535, 123]$ -

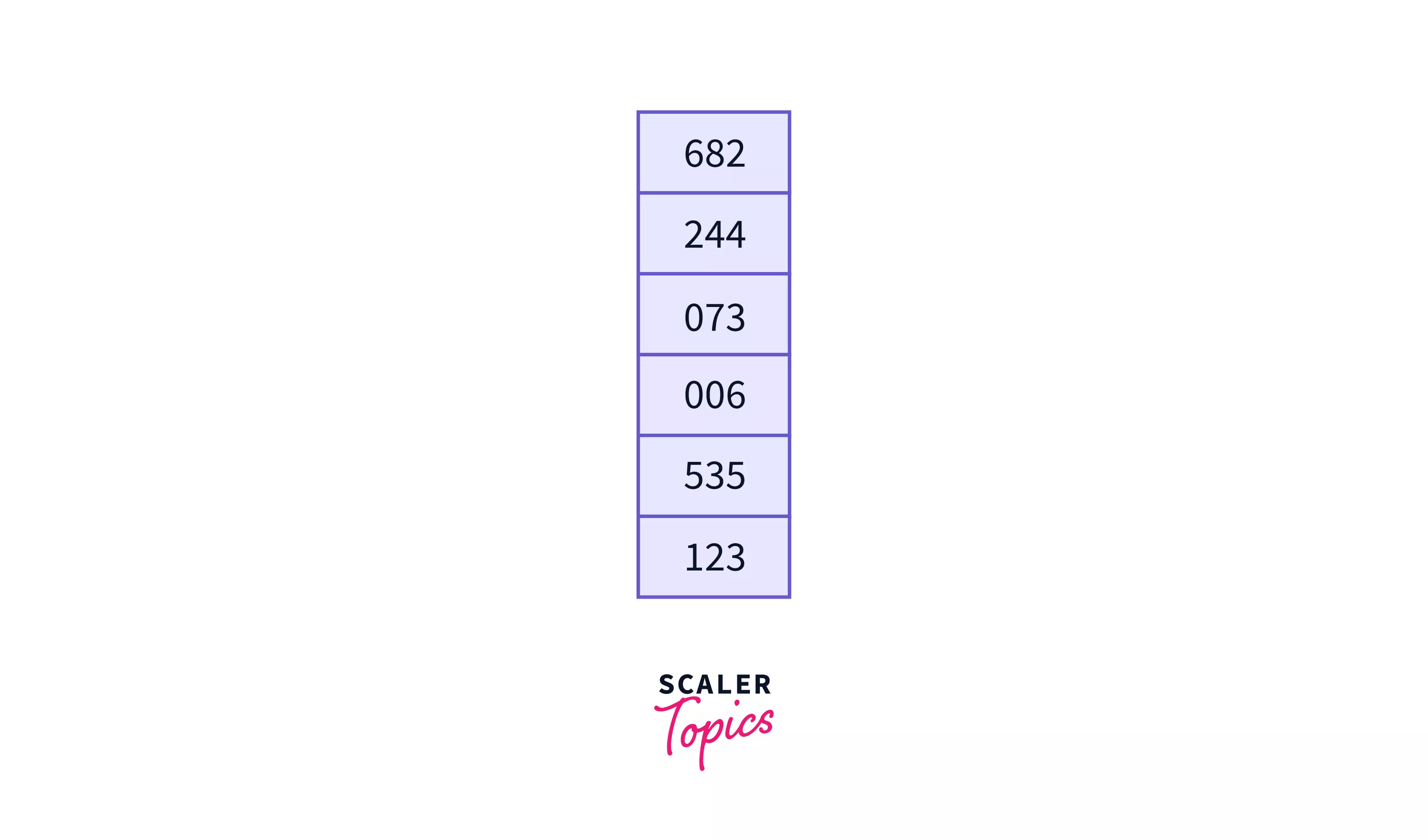
Here the maximum element is 682 which is of 3 digits, so we will apply the counting sort on the least significant digit $i.e.$ last digit -

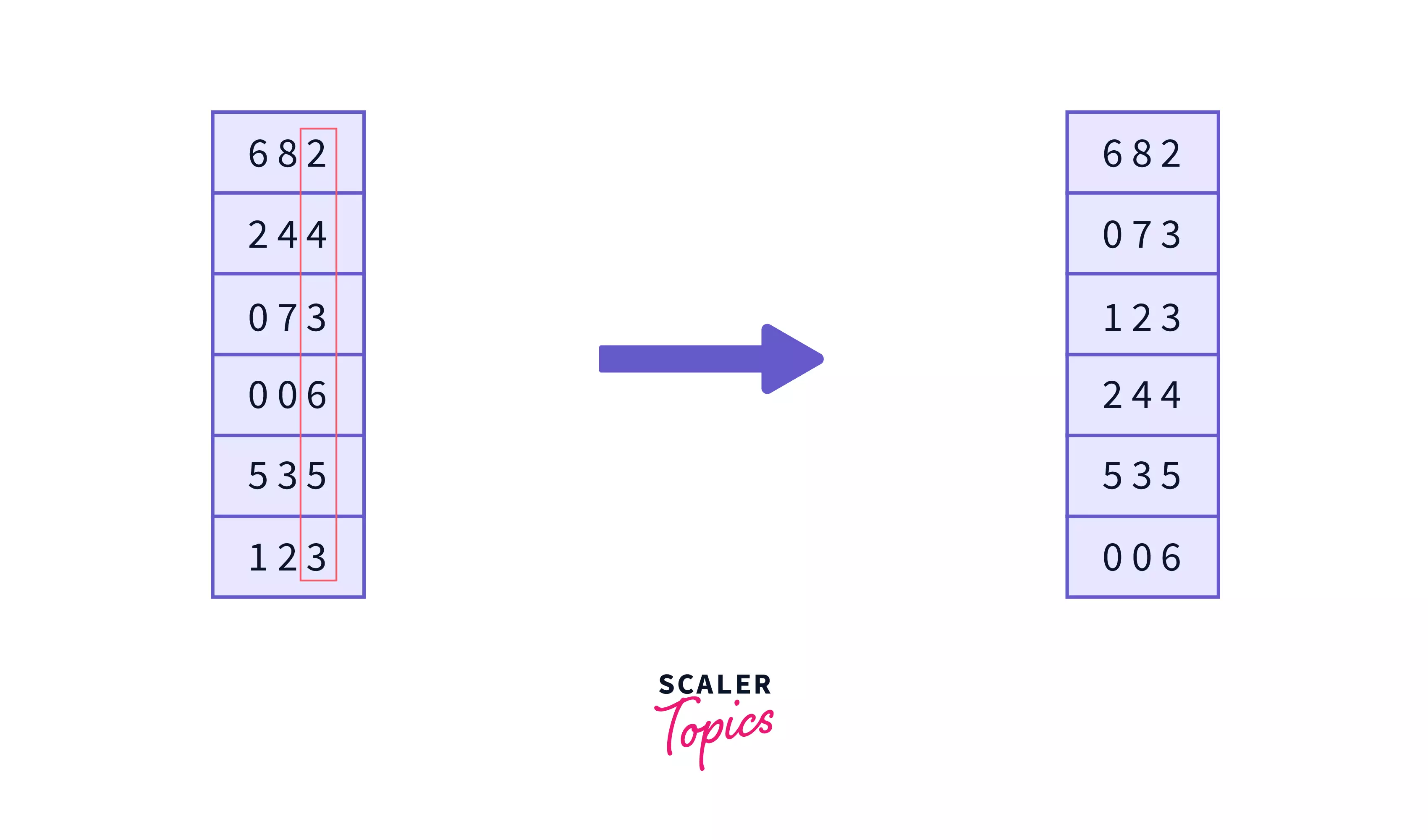
Now we apply counting sort on the second digit of the numbers, after which the numbers will get sorted on the basis of $2^{nd}$ least-significant digits -

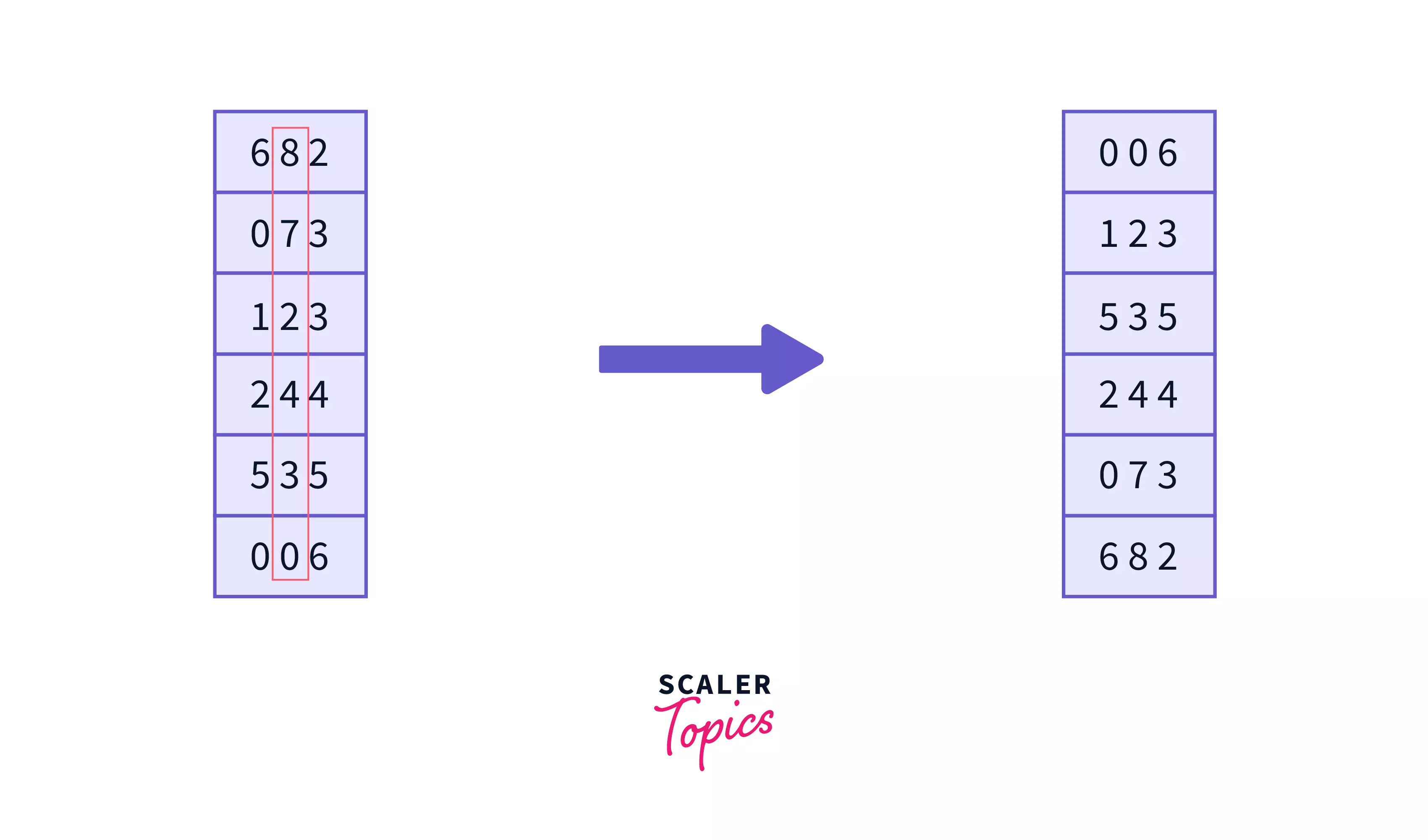
Now it's time to sort the numbers based on the $3^{rd}$ digit from right $i.e.$ the Most-significant digits. -

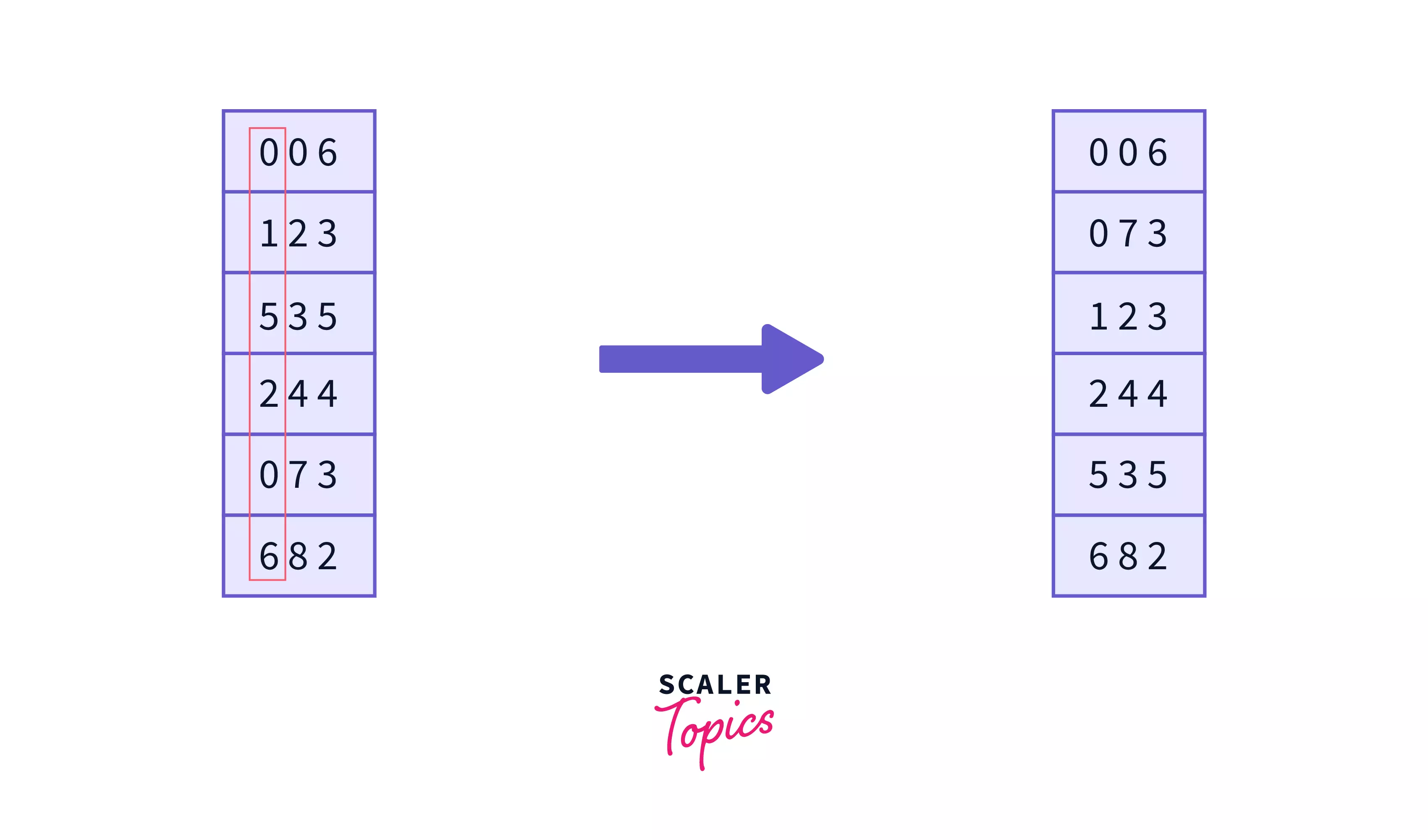
And it's done, now the array is sorted in ascending order.

Pseudocode of the Radix Sort

In pseudocode, we will be having the function RadixSort which is the main function implementing the Radix sort functionality.

Firstly, the maximum element of the array is determined, then countingSort function is called $k$ times where $k$ is the number of digits in the maximum element found in the previous step.

Implementation of Radix Sort

For implementing the radix sort algorithm we will be using two functions -

• radixSort - It takes an array (say $a$) and its size (say $n$) as arguments. Firstly, the maximum element ($max$) present in $a$ is determined, then countingSort is called with a variable div till $max/div>0$ where $div$ is multiplied by $10$ after each iteration.
• countingSort - It takes an array ($a$), size ($n$), and $div$ as arguments. Counting sort will sort the array based on the result obtained from $(a[i]/div)\%10$. Where $(a[i]/div)\%10$ in each iteration corresponds to $k^{th}$ digit of $a[i]$ where $1\leq k\leq x$.

Here $x$ denotes, the number of digits present in $max$.

C/C++ Implementation of Radix Sort

Java Implementation of Radix Sort

Python Implementation of Radix Sort

Applications of Radix Sort

• It is highly beneficial to run the Radix sort on parallel machines, making the sorting process super-fast.
• It is also used in constructing the suffix_array (An array that contains all possible suffixes of a string in sorted order.)

For example, If str="radix" then suffix array will be -

• suf[0]="adix"
• suf[1]="dix"
• suf[2]="ix"
• suf[3]="radix"
• suf[4]="x"

See More

• Radix Sort Program in C