Spanning Tree
Learn via video course

Overview
A spanning tree is a sub-graph, that contains all the vertices of a graph. A Spanning tree may or may not be weighted, a spanning tree does not have cycles and it cannot be disconnected. The Spanning tree has a minimal set of edges. A single connected graph can have multiple spanning trees.
Scope
In this article, we are going to learn about the spanning trees and their interesting properties. We will also learn about the minimum spanning tree, its properties, and algorithms to construct the minimum spanning tree with complexity analysis of the minimum spanning tree algorithm. We will discuss various real-life applications of the spanning tree as well as the minimum spanning tree (MST). We will talk about what is clustering and how it can be achieved.
What is Spanning Tree?
A spanning tree is a sub-graph that connects all the vertices of a graph with the minimum possible number of edges. It may or may not be weighted and does not have cycles.
Let us understand what is spanning tree with an interesting example.
Consider a situation where a cable television network company is laying the cable to a new neighborhood. If the company is constrained to bury the cable only along certain paths for example along the roads then the problem is to find the minimum amount of cable that the company requires to complete the wiring of the television network
The above problem can be solved by representing the cable T.V. network as a graph whose points are connected by those paths. Some of those paths might be more expensive because they are longer and require more amount of cable to be buried. These paths would be represented by the edges of a graph with larger weights.
A spanning tree for that graph would be a subset of those paths that has no cycles but still connects to every house. There might be several spanning trees possible. A minimum spanning tree would be one with the lowest total cost and thus would represent the least expensive path for laying the cable.
Spanning Trees of a given graph G can also be defined as a minimal set of edges that contains all the vertices of G. A spanning tree does not have any cycle and it can never be disconnected. A spanning tree can be weighted or unweighted.
Example of Spanning Tree
A complete undirected graph G can have a maximum nn-2 number of spanning trees, where n is the number of nodes in a given graph G. Let us Consider a complete graph G with 3 vertices, then the total number of spanning trees this graph can have is 3(3-2)=3 which are shown in the image below.
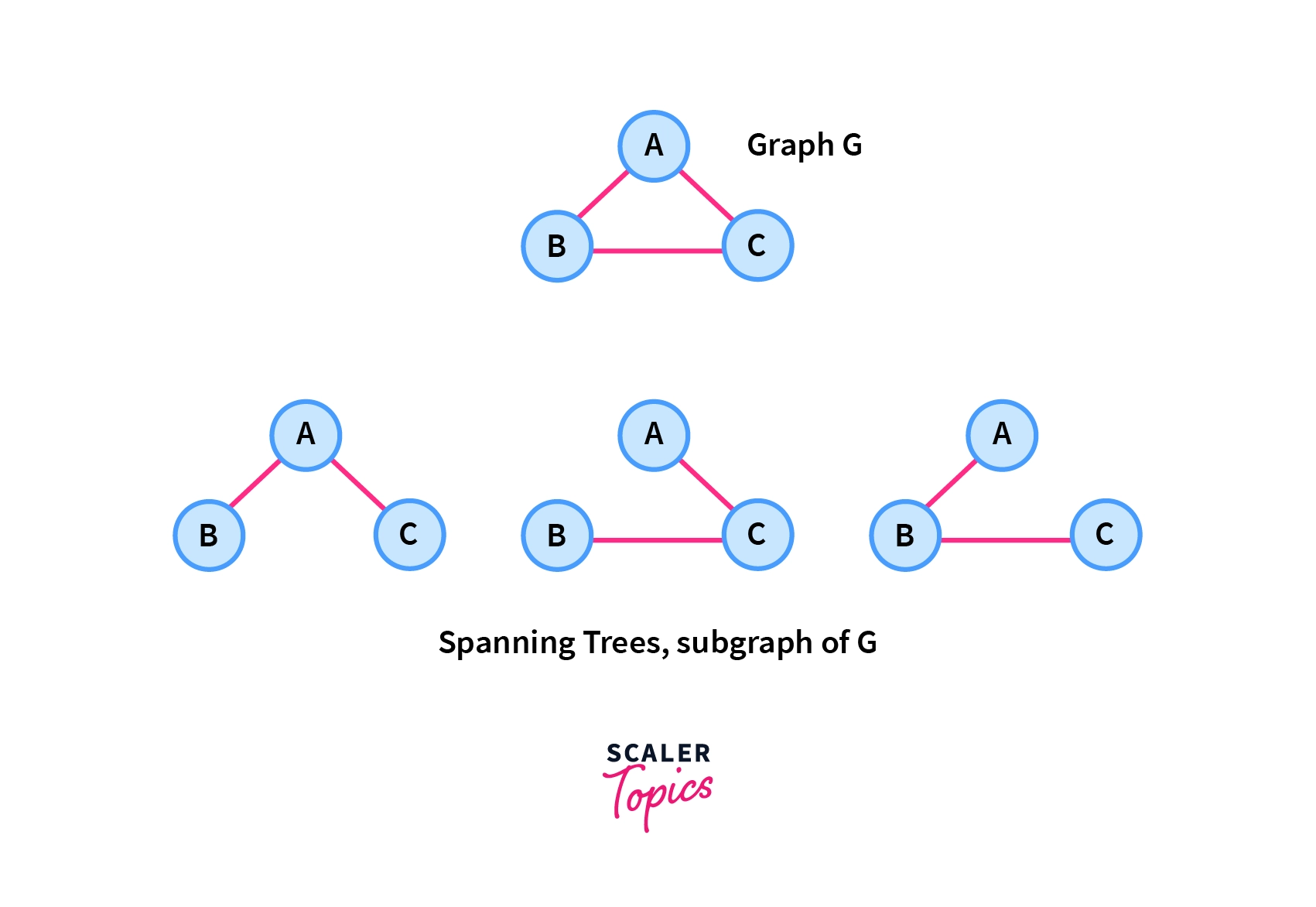
In the above picture, we can see that the tree have no cycles and they are minimally connected so they are all the possible spanning trees of 3 vertices for a given graph G.
General Properties of Spanning Tree
Let us discuss some properties of a spanning tree.
- All possible spanning trees for graph G have the same number of edges and vertices.
- Spanning trees do not have any cycles.
- A Spanning tree is a minimally connected sub-graph, which means if we remove any edge from the spanning tree then it becomes disconnected.
- A Spanning tree is a maximally acyclic sub-graph, which means if we add an edge to the spanning tree then it becomes cyclic.
- A connected graph G can have more than one spanning tree.
Mathematical Properties of Spanning Tree
Let us see some mathematical properties of a spanning tree.
- A Spanning tree always contains n-1 edges, where n is the total number of vertices in the graph G.
- The total number of spanning trees that a complete graph of n vertices can have is n(n-2).
- We can construct a spanning tree by removing atmost e-n+1 edges from a complete graph G, where e is the number of edges and n is the number of vertices in graph G.
Clustering
Let us understand clustering with an interesting example.
Consider a situation where a businessman is trying to get the best return on his marketing investment, in such a case it is crucial that he must target people in the right way. Clustering algorithms are able to group together people with similar traits and likelihood to purchase. Once he has the groups, he can run tests on each group with different marketing copy that will help him better target his customers.
Clustering is the process of grouping similar objects together. Clustering is one of the most famous applications of the spanning tree. In clustering, our goal is to divide n objects into k different groups such that the different groups get placed at maximum distance from one another.
Clustering is the task of dividing the data points into a number of groups such that data points in the same groups are more similar than those in other data points in the same group than those in other groups. In simple words, the aim is to segregate groups with similar traits and assign them into clusters.
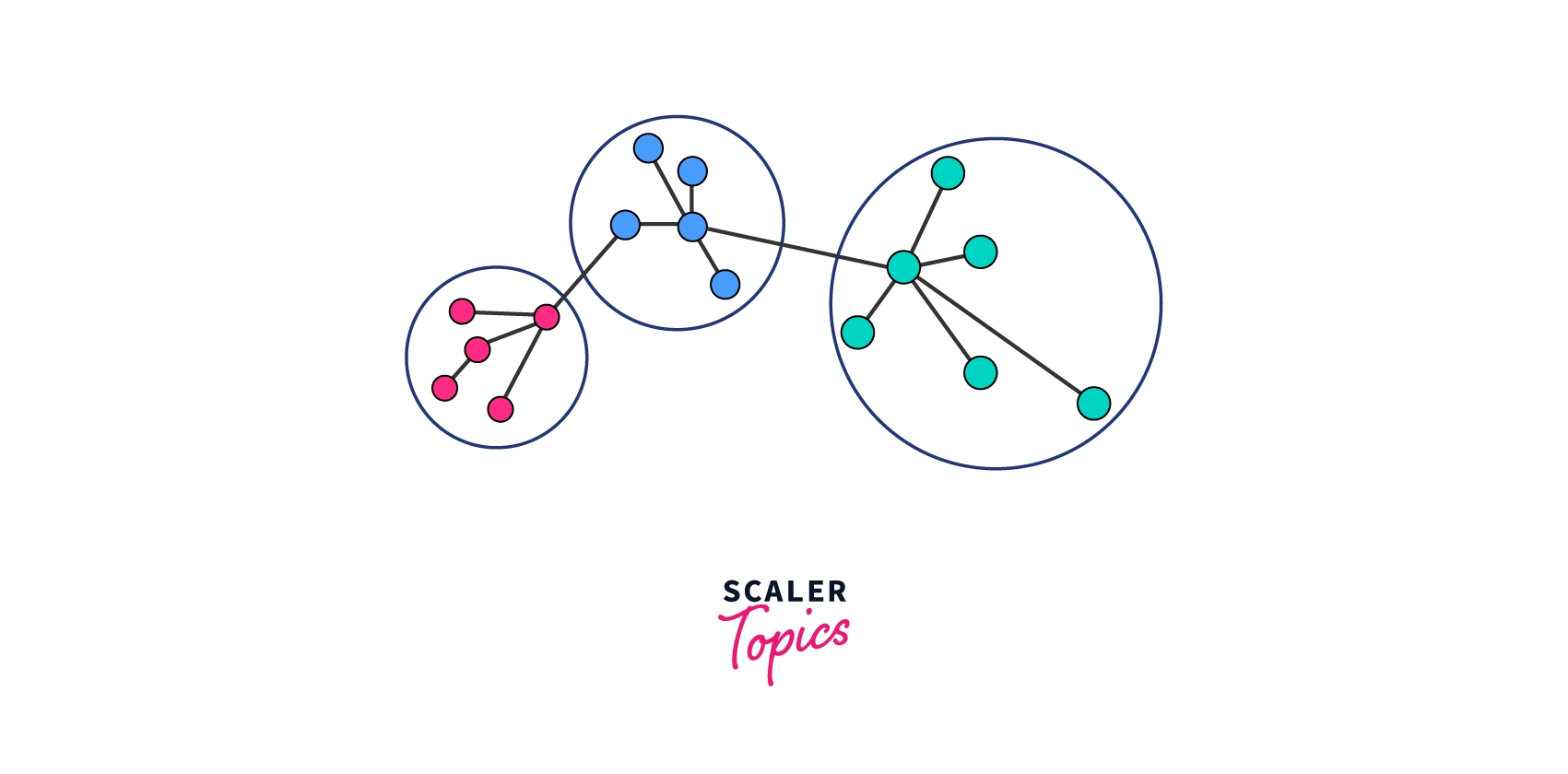
In the above picture, we can see that the objects are divided into different clusters. Every cluster is represented by a different colour.
How Can Clustering Be Achieved?
Let us take an example to understand how we can achieve clustering.
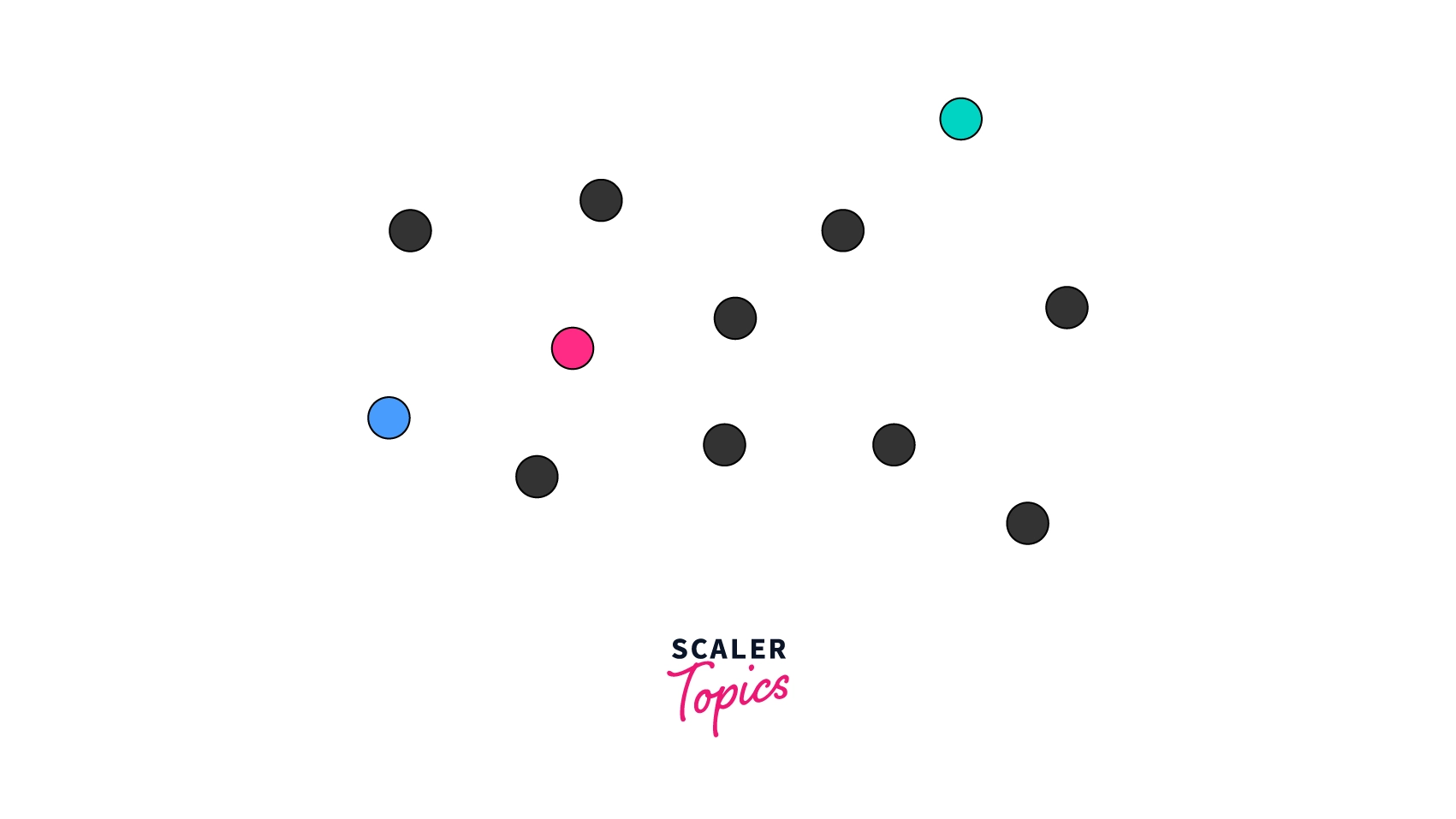
Suppose we have 12 objects and we have to divide them into 3 groups. So n=12 and k=3, where n is the number of objects and k is the number of groups in which we have to divide the n objects.
- Firstly we divide the n objects into k groups. Here n=12 and k=3.
Here every group is represented by a different color.
- Now we combine these clusters iteratively by adding an edge between them.
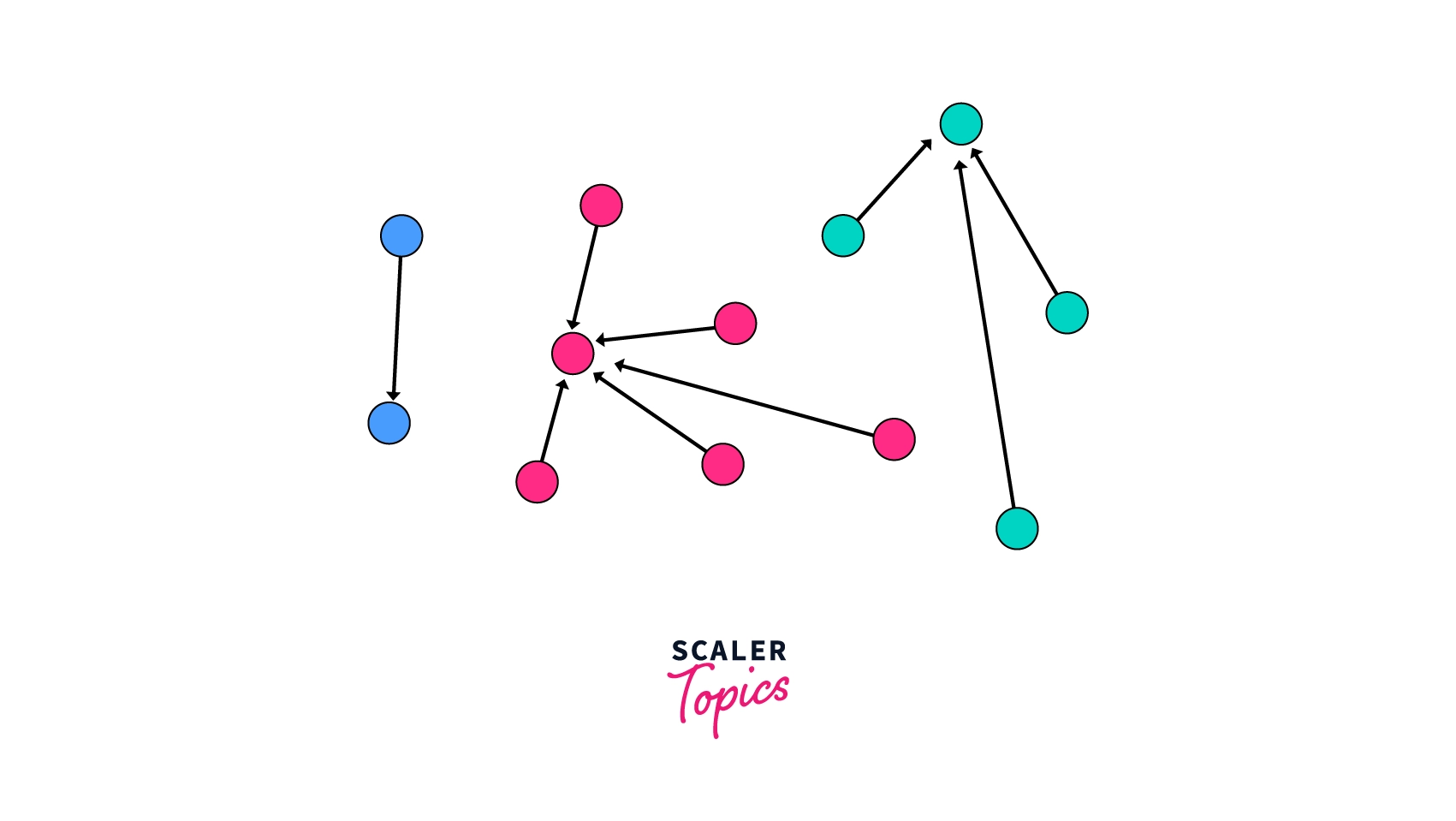
- We will stop after we reach the k clusters.
What is Minimum Spanning Tree?
Let us learn about the Minimum Spanning Tree with an interesting real-life example.
Consider a Parcel delivery Agency which delivers the parcels over the city. The company has delivery agents who deliver the parcel to different parts of the city. The goal of the company is to deliver all the parcels with the minimum cost of transportation and in the minimum amount of time. To achieve this goal company has to decide on an optimal path for every delivery agent such that it requires minimum time and fuel for delivering all the parcels.
The above problem can be solved by representing the route in form of a graph, whose vertices represent the destination of delivery, and the path to reach the destination is represented by the edges of the graph. We can have multiple spanning trees that represent the various routes of delivery In such cases a minimum spanning tree will be one by which we can reach the destination in the minimum time and cost which serves the purpose of the company.
A minimum spanning tree is a spanning tree that has a minimum cost among all the spanning trees. The cost of the spanning tree is the sum of the weights of all the edges in the tree. In real-life situations, this weight can be measured as distance, cost of transportation, manufacturing cost, traffic load, or any arbitrary value denoted by the edges. A minimum spanning tree has (V – 1) edges where V is the number of vertices in the given graph.
For a given graph G a minimum spanning tree of a graph is unique if the weight of all the edges is distinct. Otherwise, there may be multiple possible minimum spanning trees. Minimum Spanning tree can also be written as MST in short form.
Example of Minimum Spanning Tree
Let us understand the Minimum Spanning Tree with the help of the example below.
Consider a weighted graph G with three vertices as shown in the picture below.
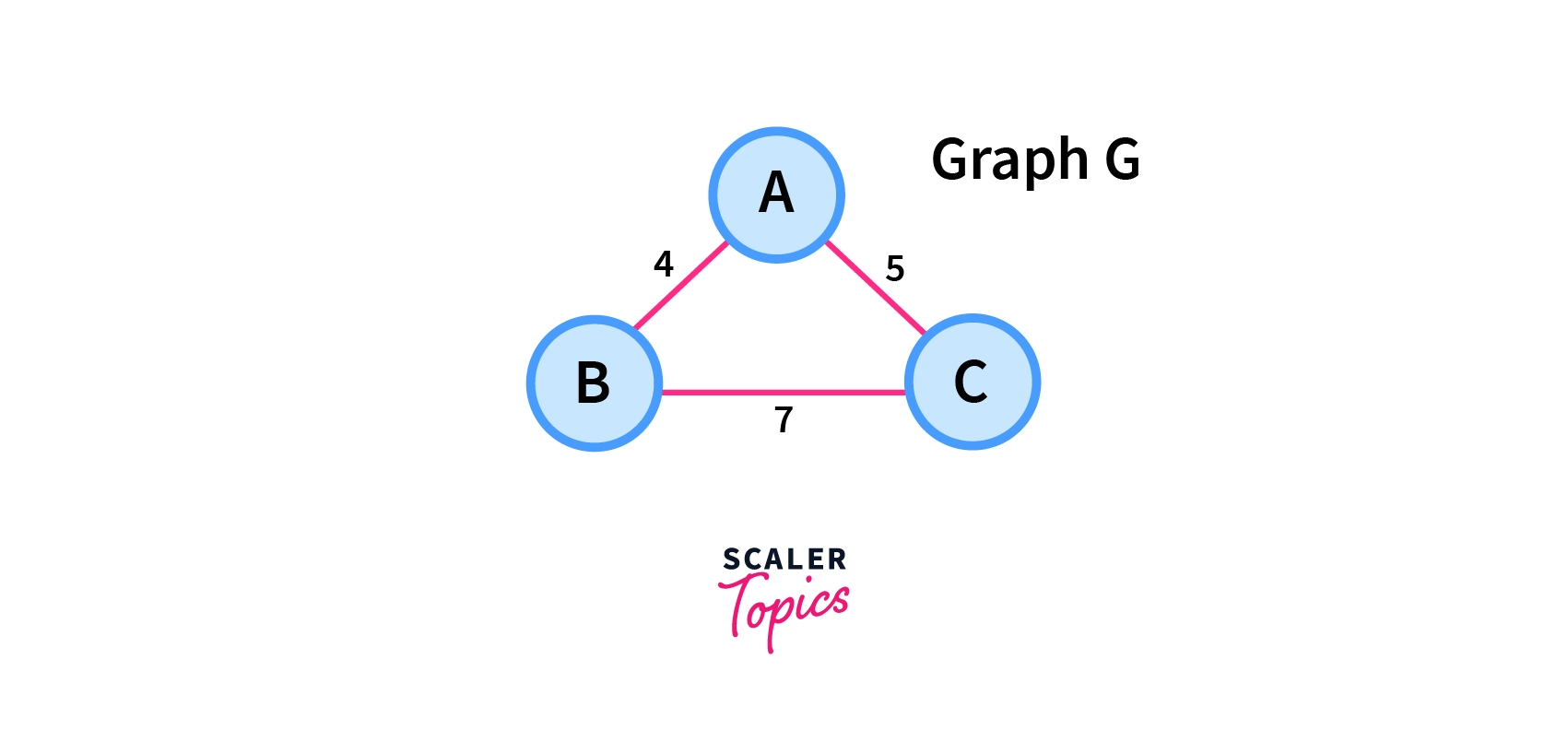
Now let us see some of the spanning trees which are possible with this graph G.
1. 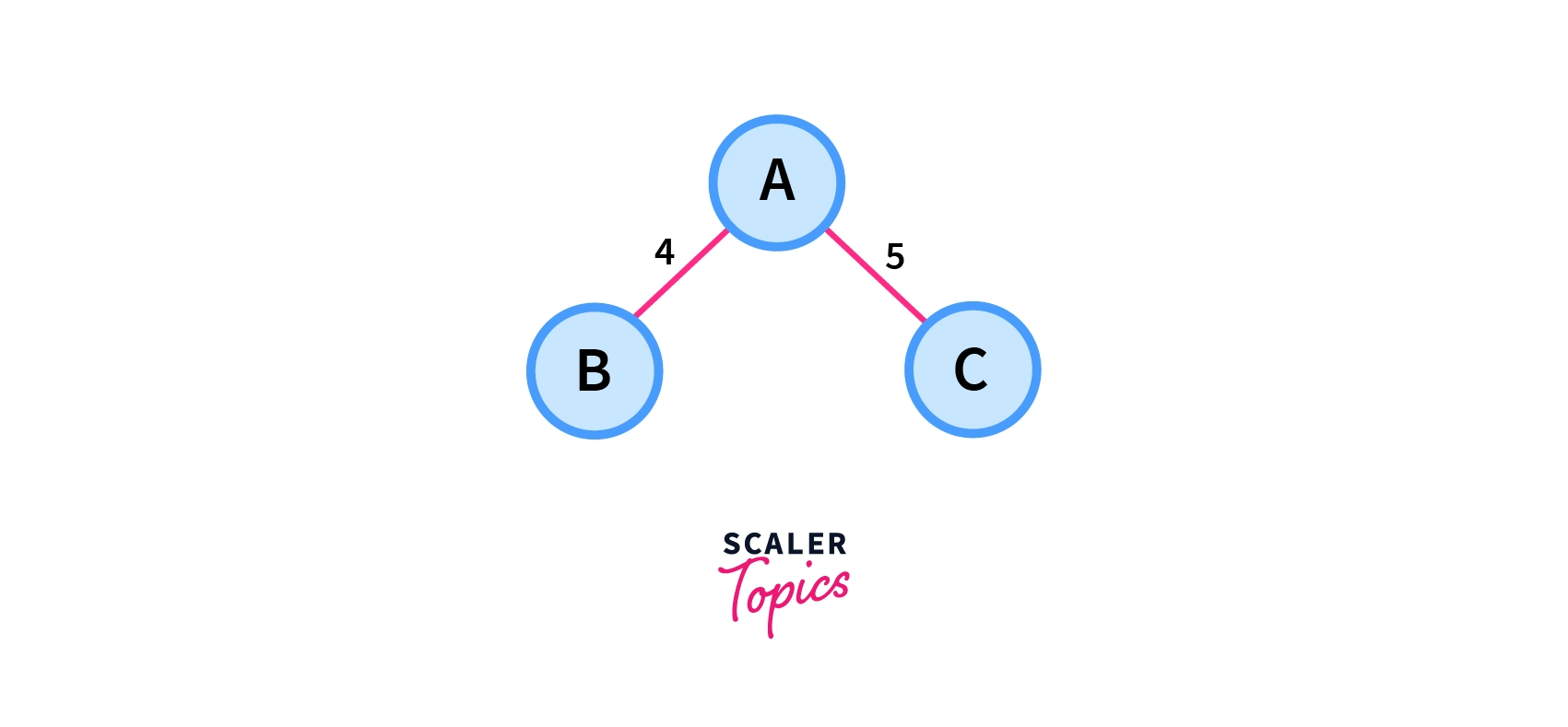
Total Cost=4+5=9
2.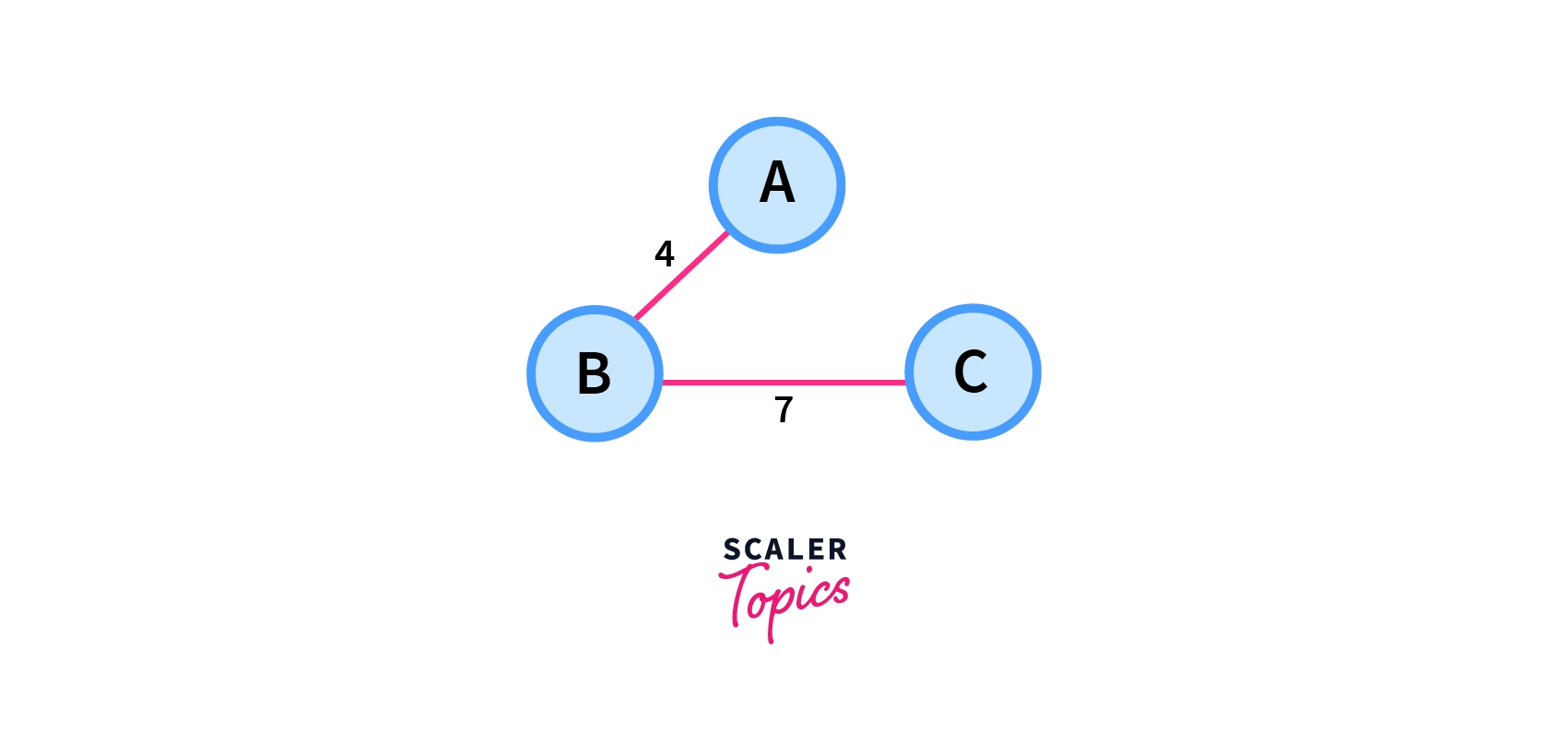
Total Cost=4+7=11
3.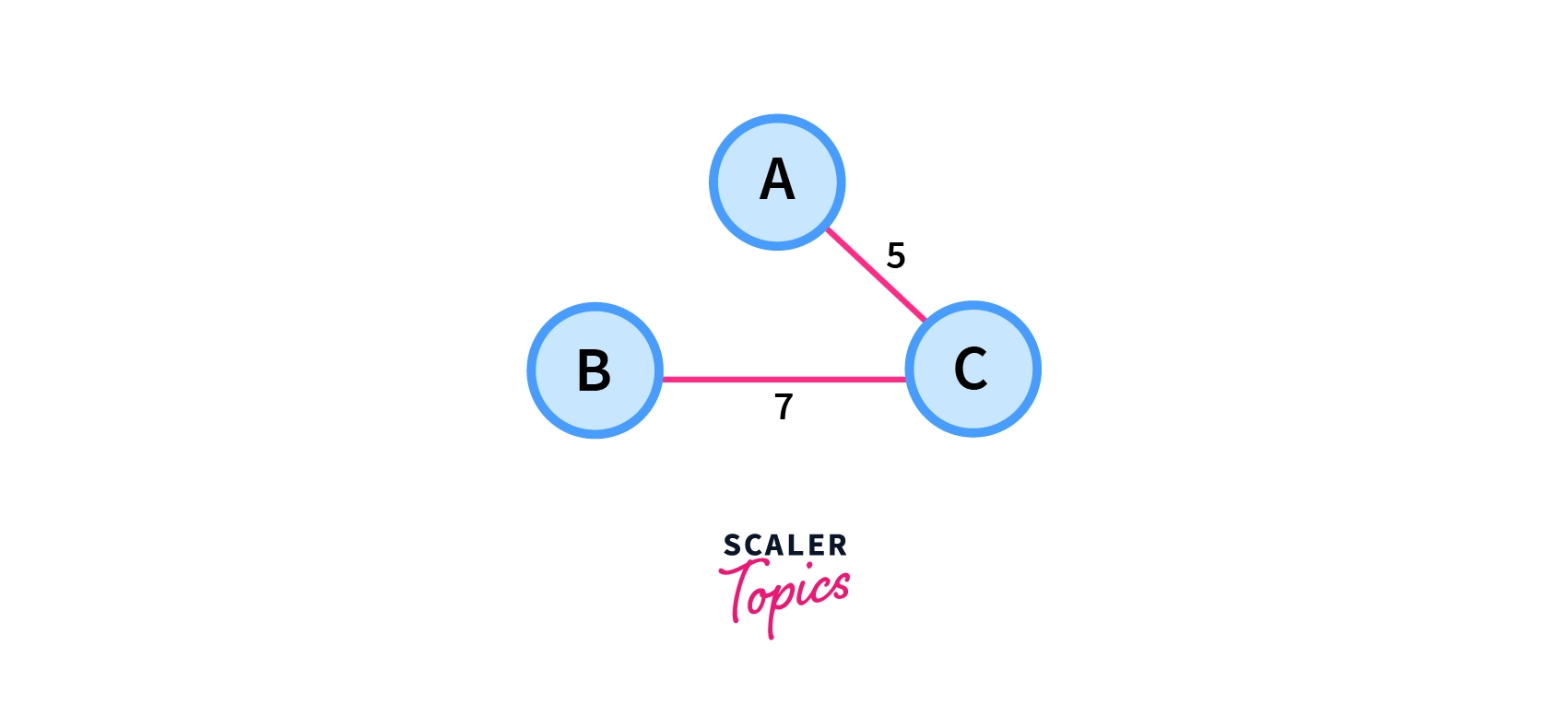 Total Cost=7+5=12
Total Cost=7+5=12
From the above three cases, we can see that among all possible spanning trees figure 1 has the minimum cost, So it is the minimum spanning tree among the given spanning trees.
Minimum Spanning Tree Algorithm
Let us study the minimum spanning tree algorithm. So there are two famous algorithms for finding the Minimum Spanning Tree: Prim's and Kruskal's Algorithm
Kruskal’s Algorithm
In Kruskal’s Algorithm, the spanning tree is constructed by adding the edges one by one. Kruskal’s Algorithm is based on the greedy approach because every time we add that edge that has the least weight among all available options.
Algorithm Steps:
- Sort all the edges of the graph in the increasing order of their weight.
- Pick the edge with the smallest weight.
- Check if it forms a cycle with the spanning tree formed so far.
- Include the current edge if it does not form any cycle.
- Otherwise discard it.
- Repeat step #3 until there V-1 edges in the spanning tree, where V is the total number of vertices in the graph.
Example
Let us understand the working of Kruskal's Algorithm with an example. Consider a weighted graph G having seven vertices in the picture below.
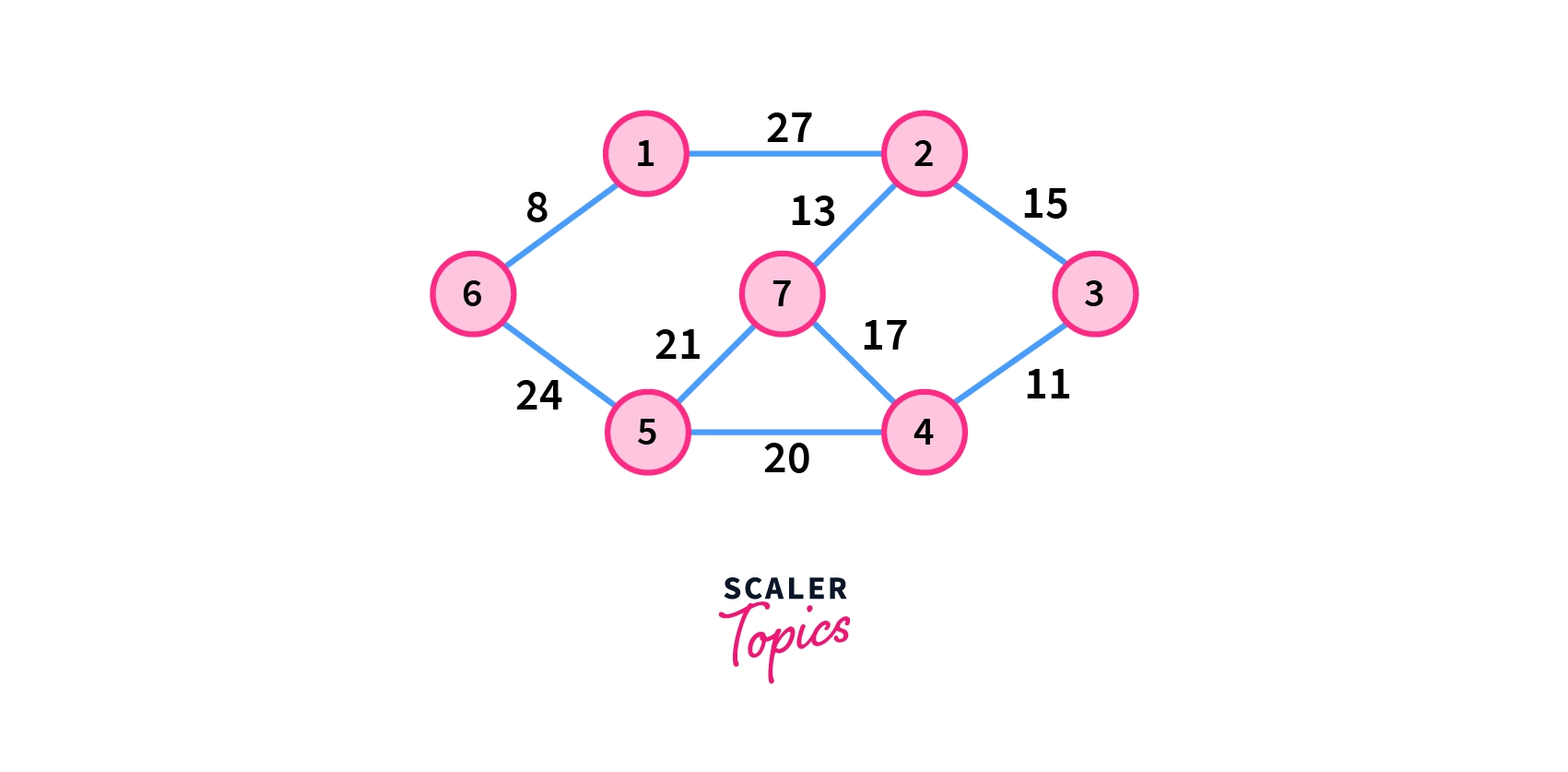
Now to find the minimum spanning tree using Kruskal's Algorithm, follow the steps below.
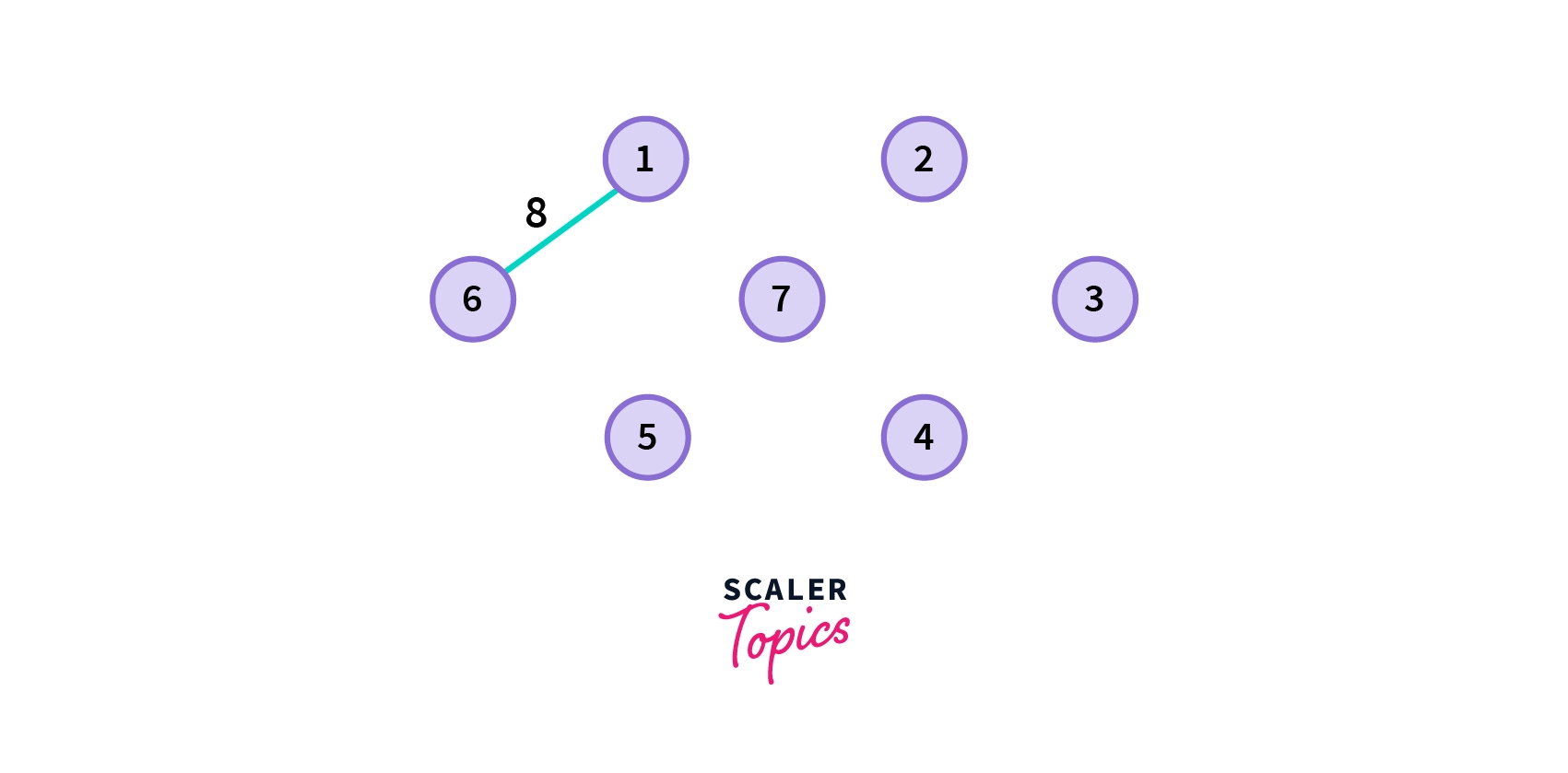
-
Choose the edge with the minimum weight.
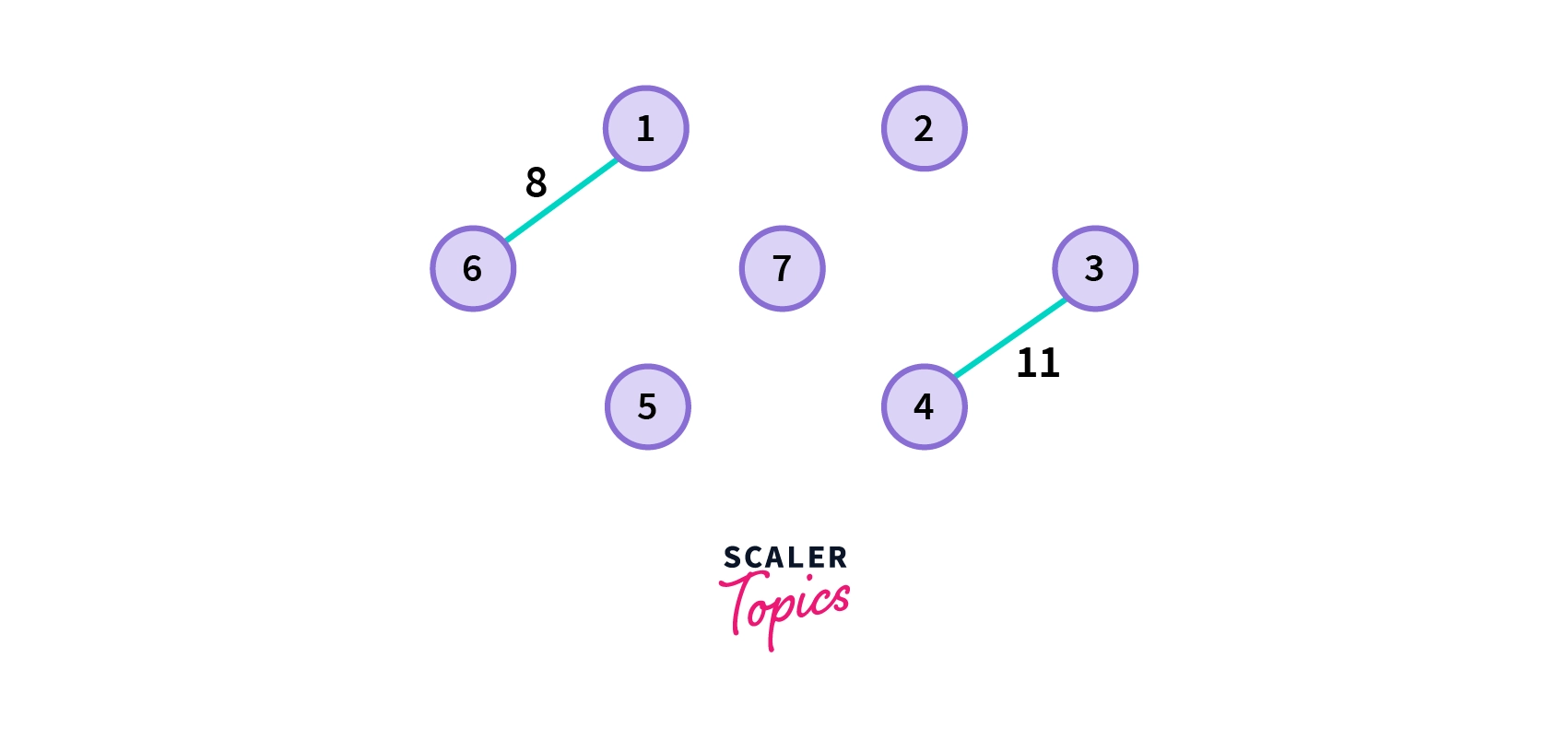
-
Choose the next shortest edge and add it. We can see from the below picture that the next shortest edge need not be connected with the former one.
- Choose the next shortest edge that doesn't create a cycle and add it.
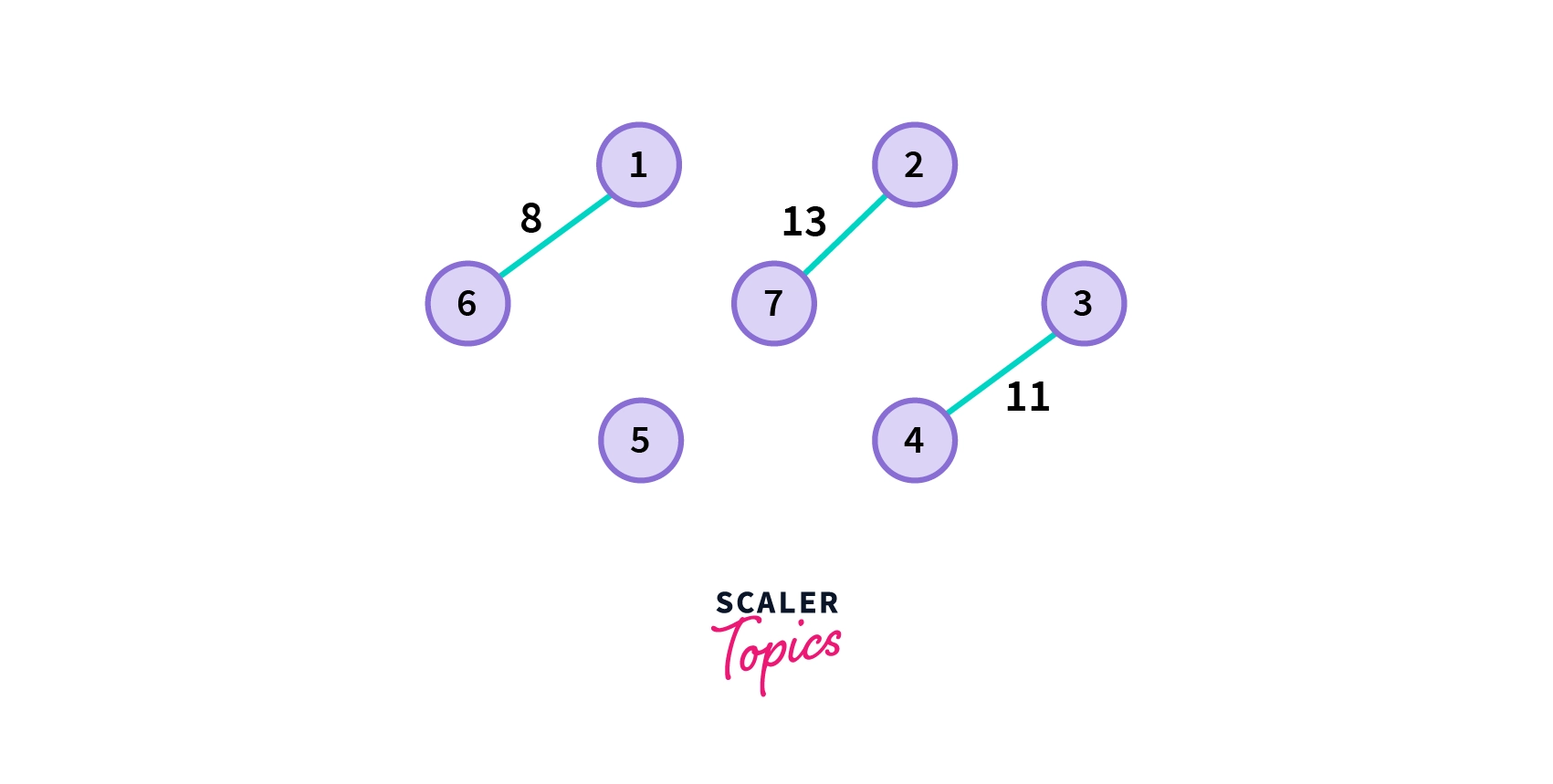
- Choose the next shortest edge that doesn't create a cycle and add it. If there are more than one such edges, choose anyone from them.
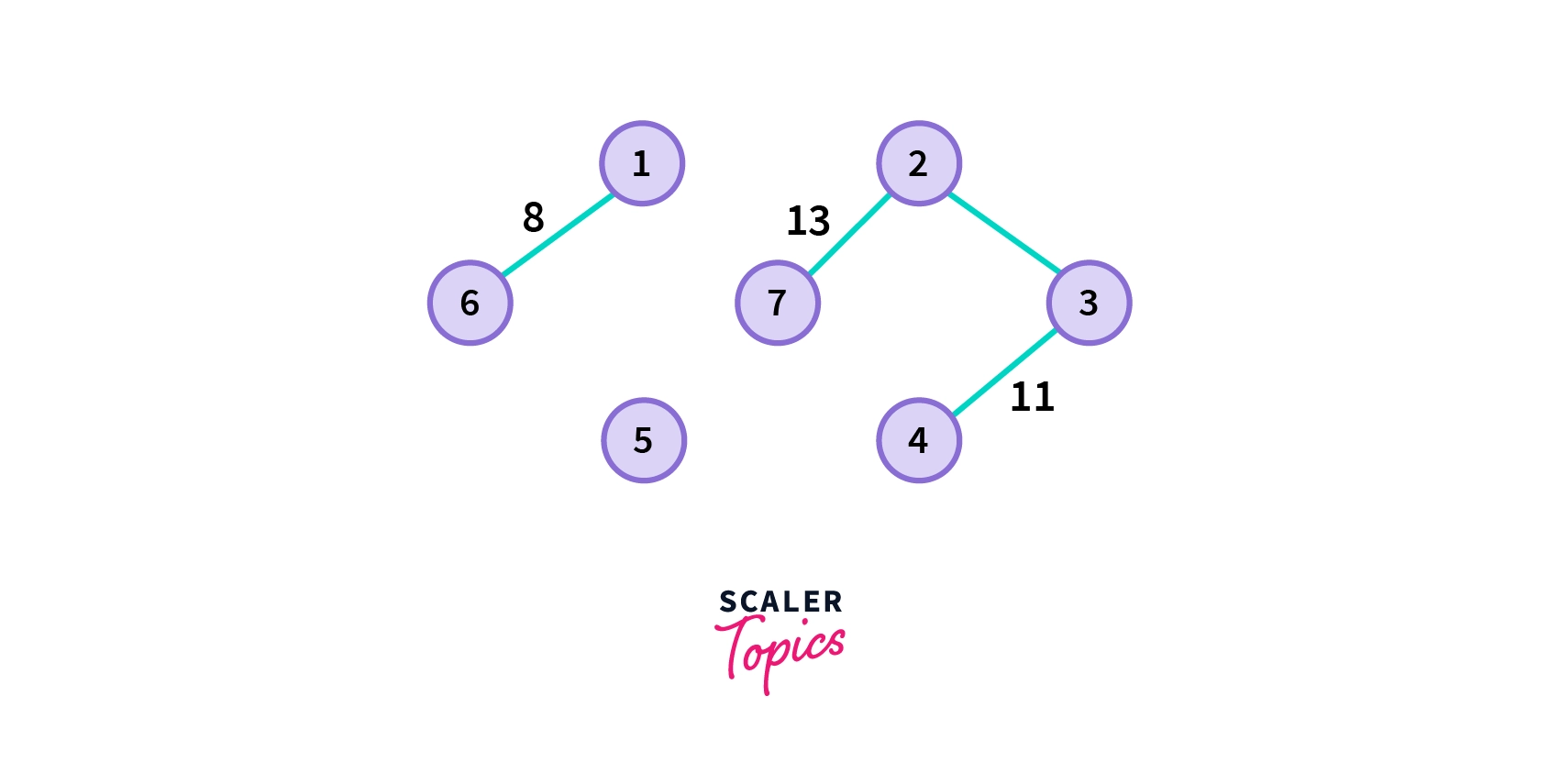
- Choose the next shortest edge that doesn't create a cycle and add it.
- Repeat step 5 until you a spanning tree.
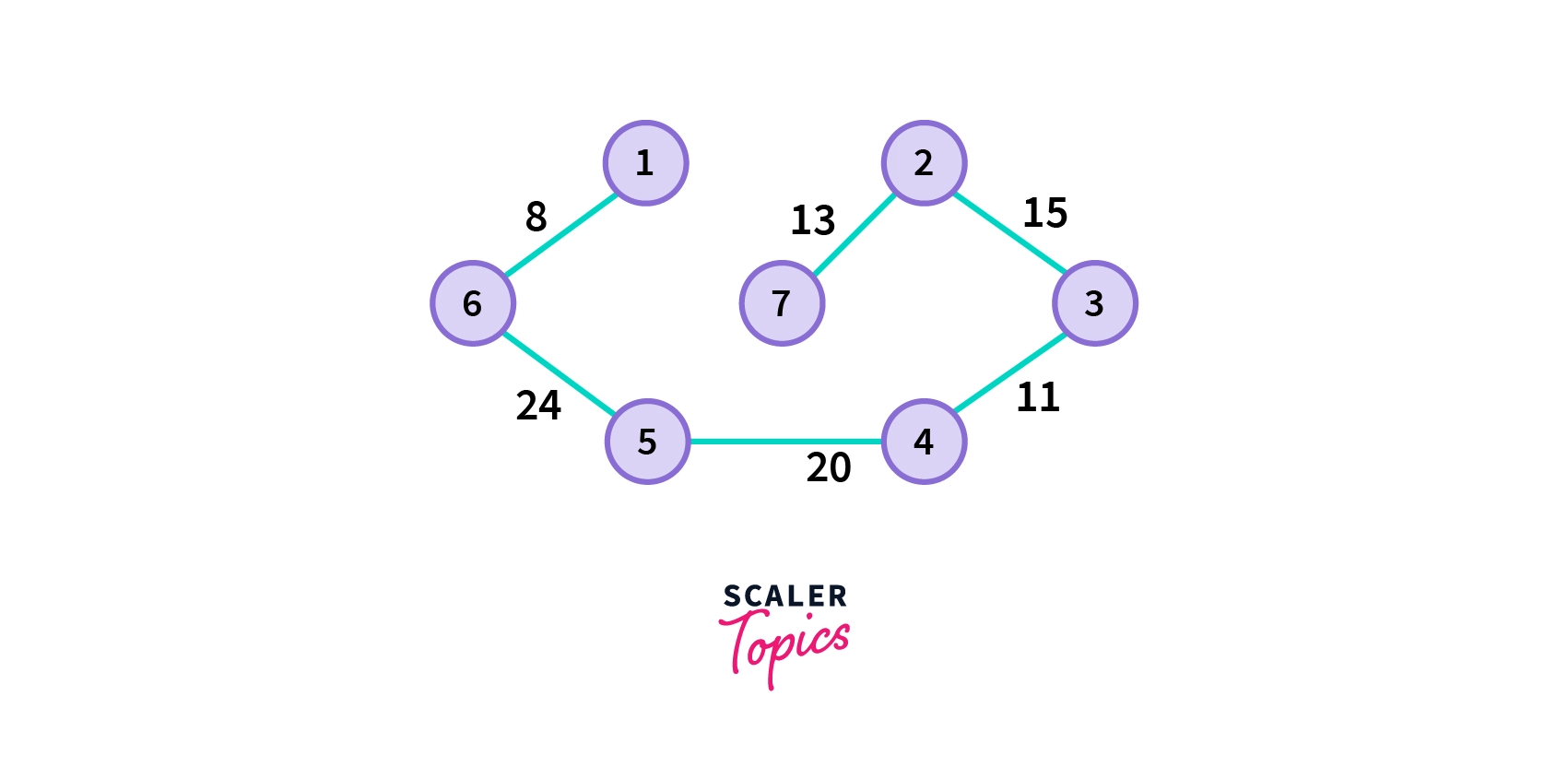
Implementation of the Kruskal's Algorithm
The Kruskal's algorithm is a Greedy Algorithm. The Greedy Choice is to pick the smallest weight edge that does not cause a cycle in the MST constructed so far. The idea is to sort all the edges of the graph in the increasing order of their weight. Then we pick the smallest edge and check if it forms a cycle with the spanning tree formed so far. If cycle is not formed,we include the current edge only if it does not form a cycle otherwise we discard the currently picked edge.
To detect if after including the current edge it will form a cycle or not we use the union finds algorithm.
Approach
Below is the step by step aproach to implement the Kruskal's algorithm.
- Create an input array to store the Edges of the Graph.
- Sort the Edges in the increasing order of their weights.
- Create an output array to represent the Minimum Spanning Tree.
- Create a parent array to Store the parent of each Vertex.
- Initially make every vertex parent of itself.
- Iterate over the input array.
- Find the Parent of the Source and Destination of the Current Edge.
- If Source Parent is not equal to the Destination Parent, then adding the Current Edge will not form any Cycle.
- Print the Minimum Spanning Tree which is represented by the output array.
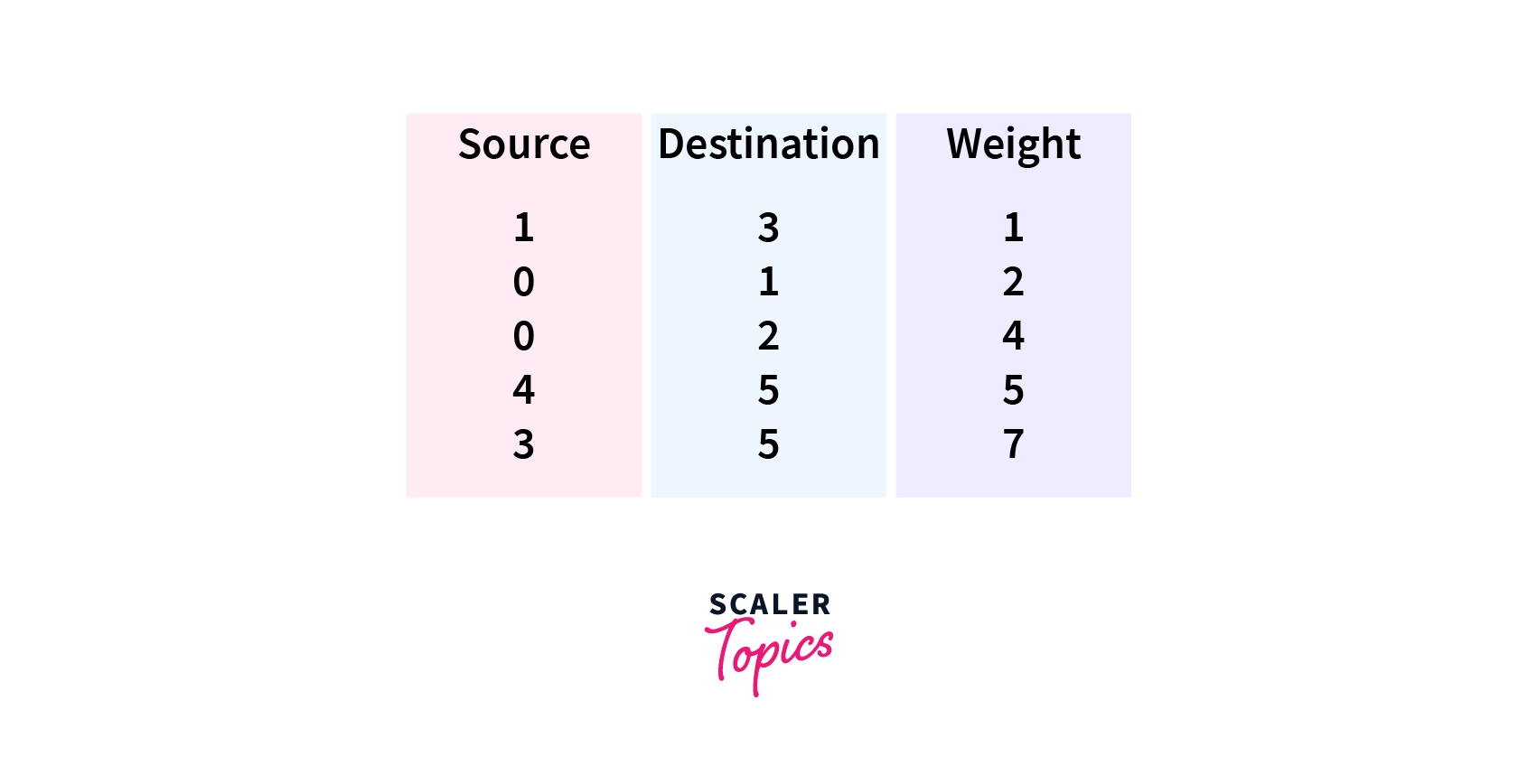
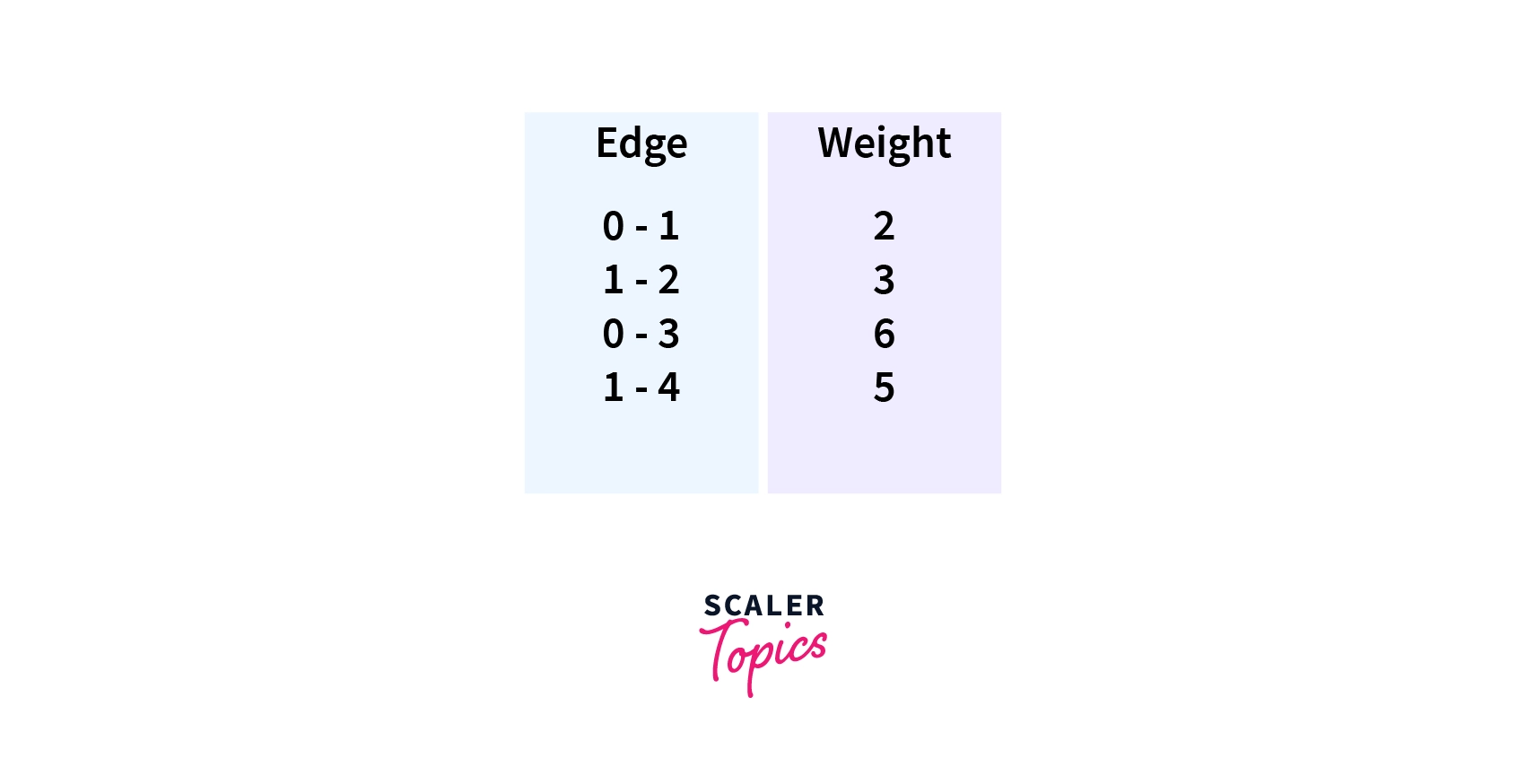
Here is the C++ implementation of the above approach
Input of Above Code
Output of Above Code
Prim's Algorithm
Like Kruskal’s Algorithm, Prim's Algorithm is also used to find the minimum spanning tree from a graph. In Prim's algorithm, we find the subset of edges that includes every vertex of the graph in such a manner that the sum of the weights of the edges can be minimized.
Unlike Kruskal's algorithm, Prim's algorithm treats the nodes as a single tree and keeps on adding new nodes to the spanning tree from the given graph.
Algorithm Steps:
- Select a starting vertex.
- Select an edge e connecting the tree vertex and fringe vertex that has minimum weight. Fringe vertices are the vertices adjacent to visited vertices but not yet visited.
- Add the selected edge and the vertex to the minimum spanning tree T
- Repeat step #2 and step #3 until the vertices adjacent to the visited vertex are unvisited.
Example
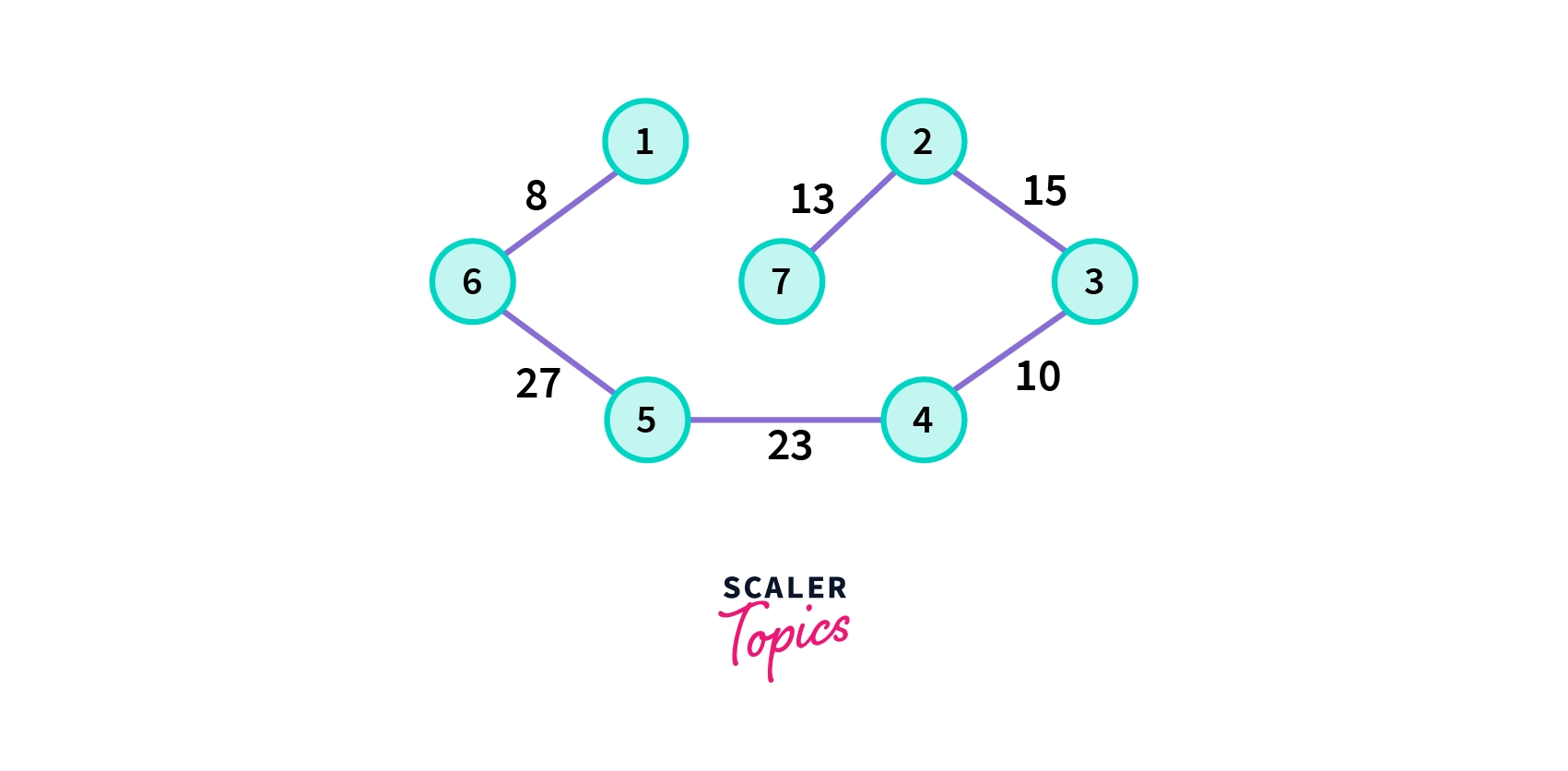
Let us understand the working of Prim's Algorithm with an example. Consider a weighted graph G having seven vertices in the picture below.
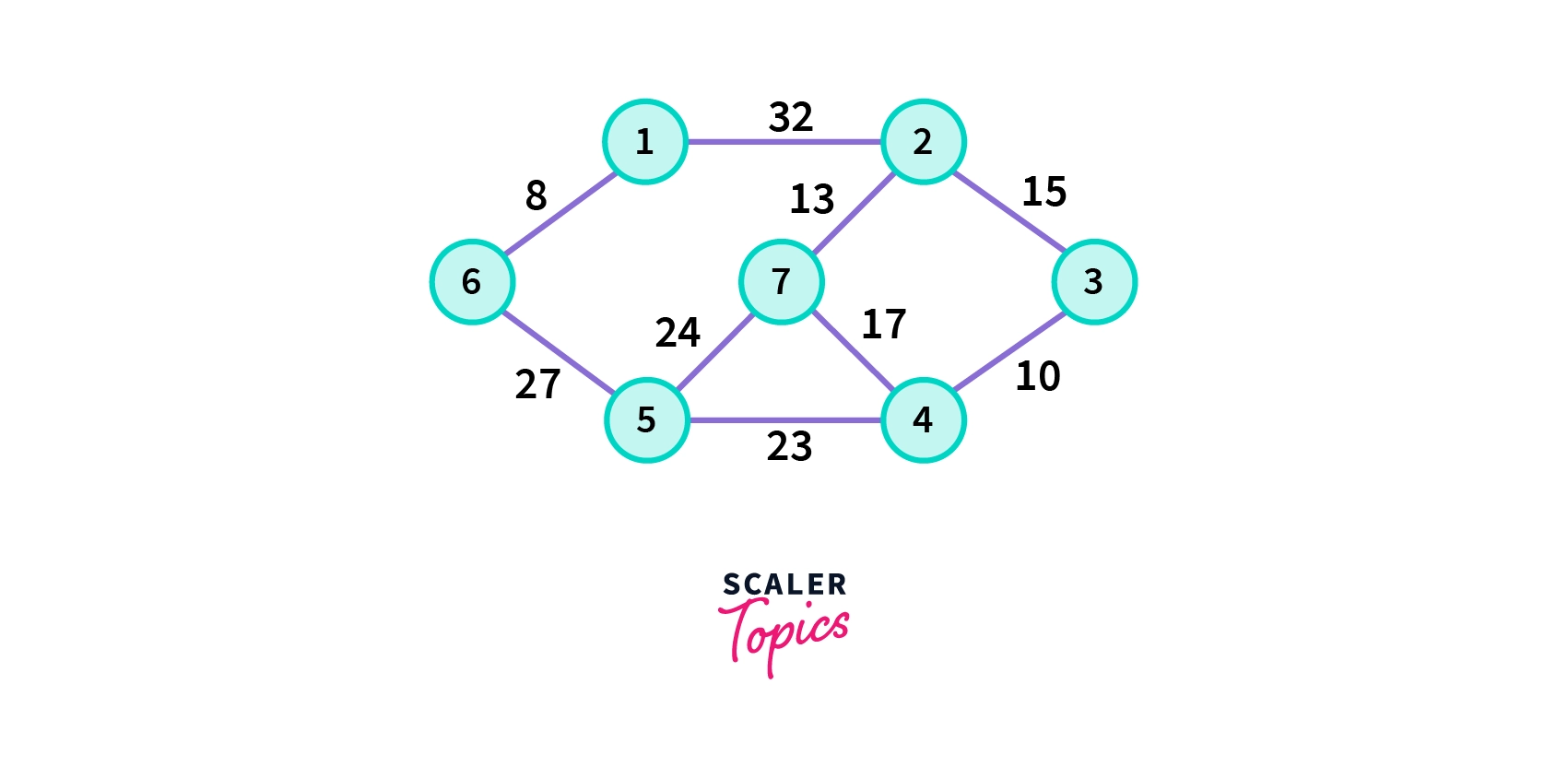
Now to find the minimum spanning tree using Prim's Algorithm, follow the steps below.
- Choose any arbitrary vertex , here we are starting from vertex 1 in the given graph G.
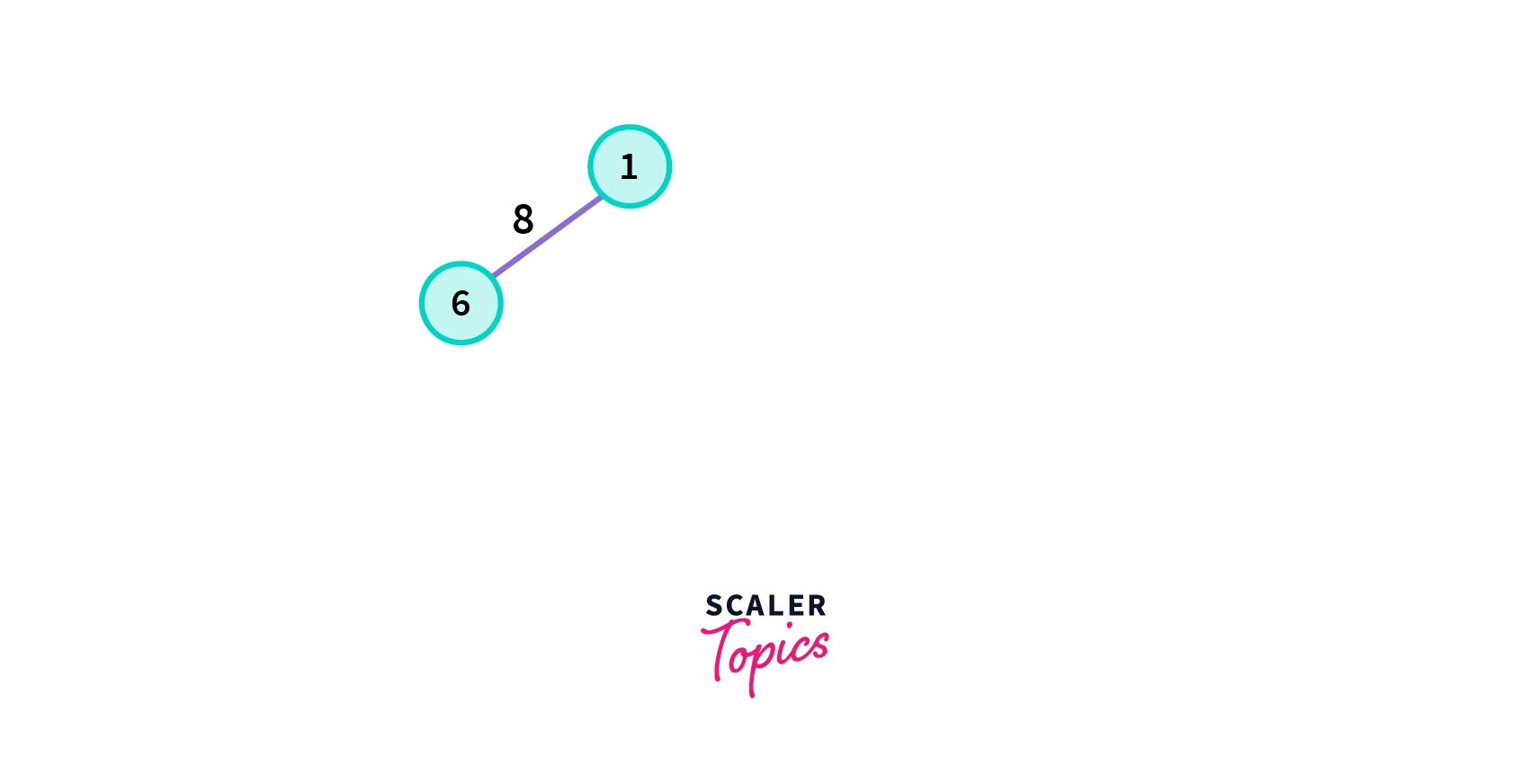
- Choose the shortest edge from this vertex and add it to the spanning tree so formed.
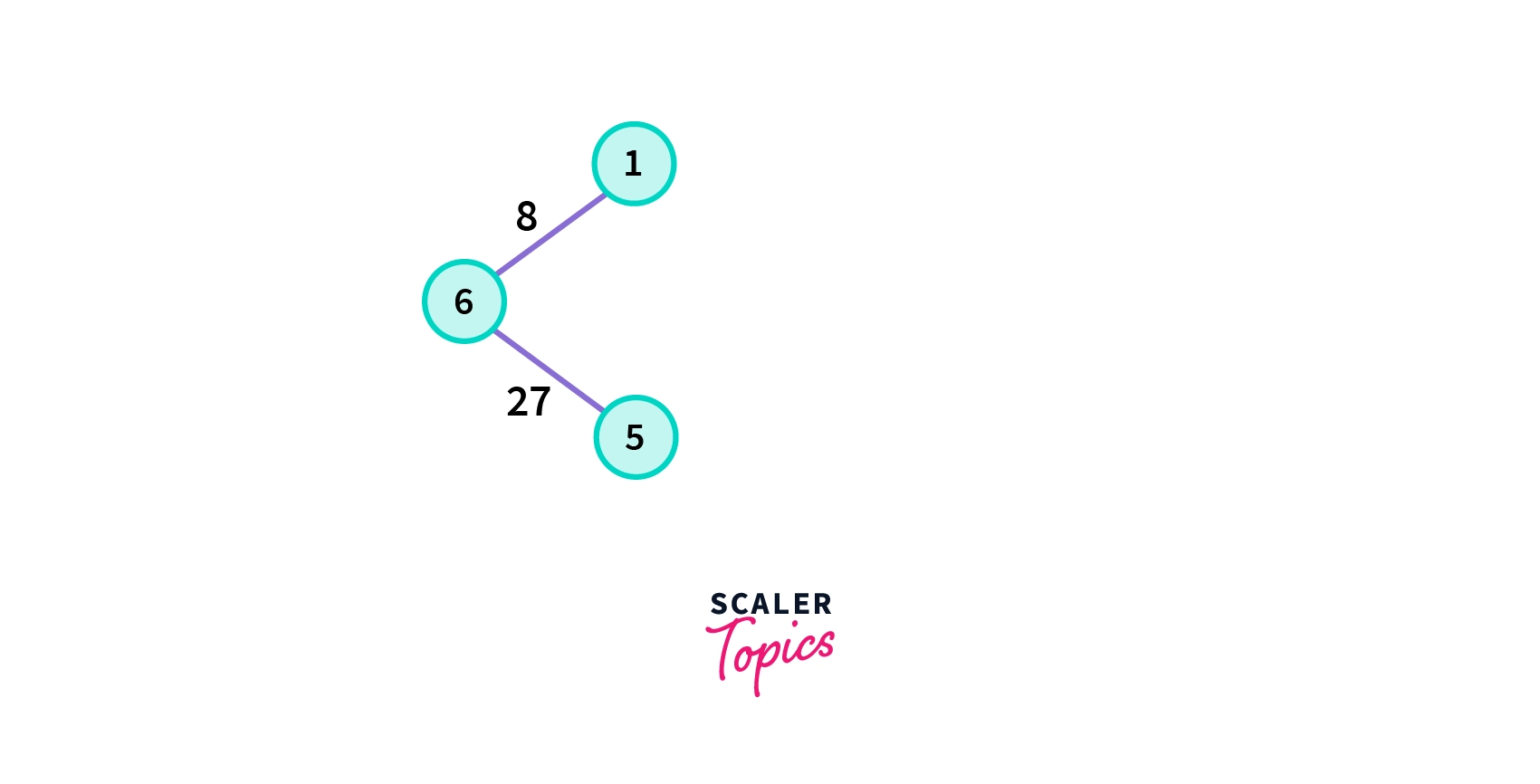
- Choose the nearest vertex which is not yet included in the solution. In each iteration, we are considering all the respective fringe vertices for a particular vertex.
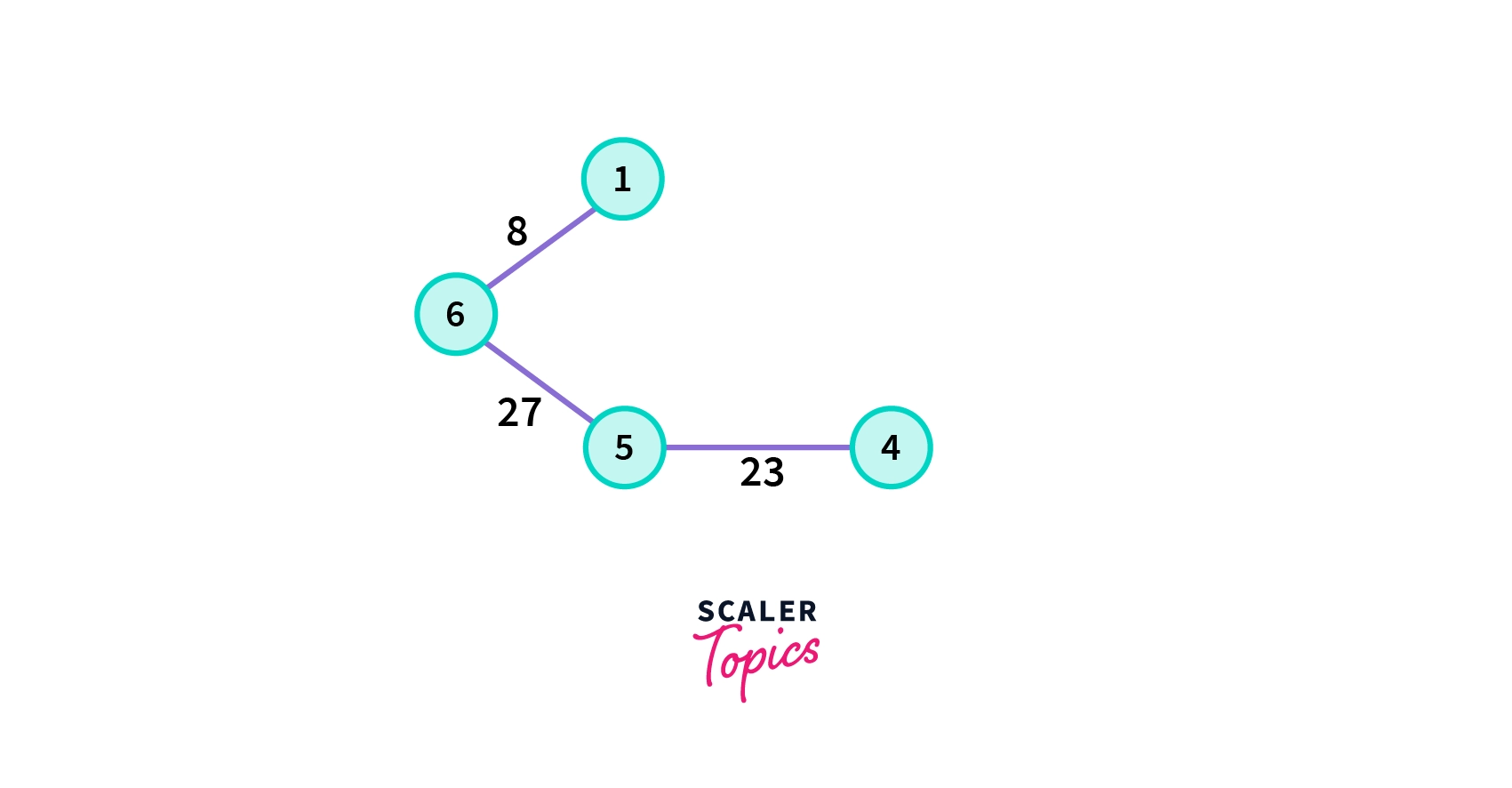
- Choose the nearest vertex which is not yet included in the solution and does not form any cycle.
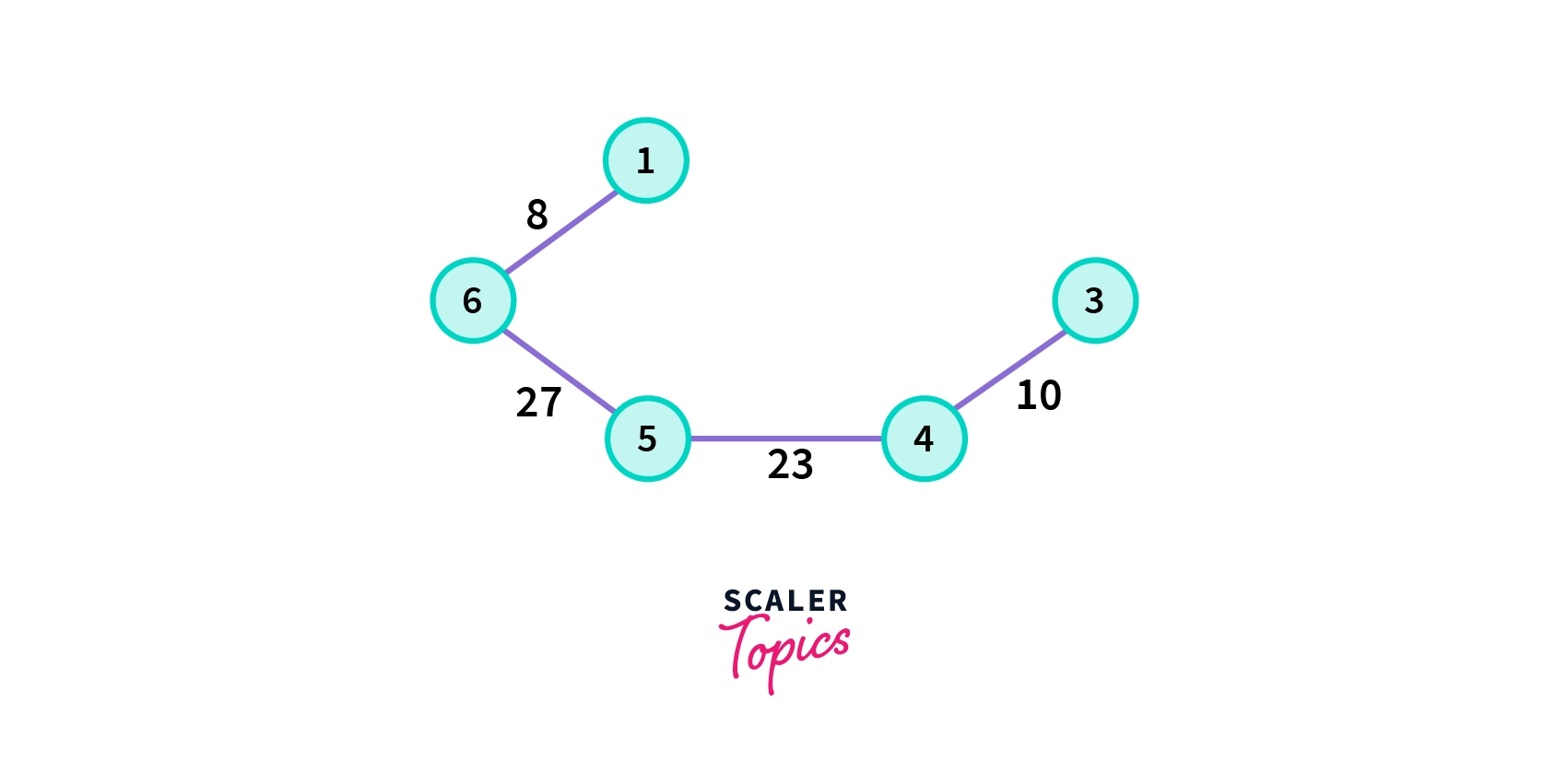
- Choose the nearest vertex which is not yet included in the solution and does not form any cycle.
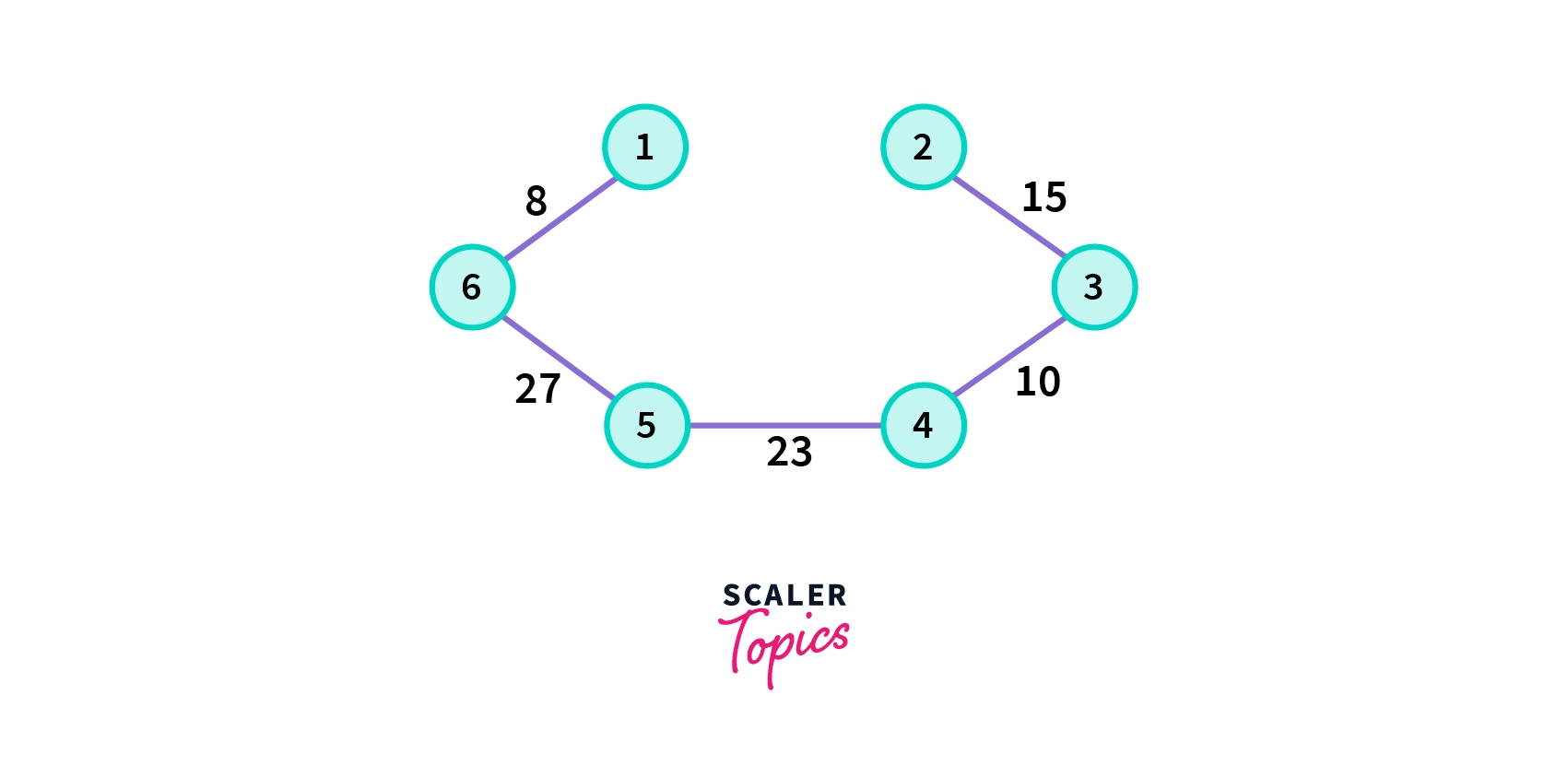
- Repeat the same process until our minimum spanning tree does not have V-1 vertices, where v is the total number of vertices in the in original graph G.
Implementation of the Prim's Algorithm
In Prim’s algorithm, we find a cut that consists of two sets, one set contains the vertices already included in MST and the other contains the rest of the vertices which are not yet included in the MST, then we pick the minimum weight edge from the cut and include this vertex to MST Set that contains the set of vertices which are already visited.
Approach
Below is the step-by-step aproach to implement Prim's algorithm.
- Create an array parent[] of size V to store indexes of parent nodes in MST.
- Also create an array key[] to store key values of all vertices.
- Initialize all key values as INFINITE.
- Assign key value as 0 for the first vertex so that it is picked first.
- Create a boolean array mstSet[] to represent the set of vertices included in MST.
- While mstSet doesn’t include all vertices
- Pick a vertex u which is not there in mstSet and has minimum key value.
- Include u to mstSet.
- Update the key value of all adjacent vertices of u according to the respective edge weights.
- The parent array is the output array that is used to show the constructed MST.
Here is the C++ implementation of the above approach
Output of Above Program
Application of Spanning Tree
Spanning tree has various uses in real life some of the applications are as follows.
- Spanning Trees are used in designing networks like computer networks, telephone networks, etc.
- Spanning Trees are used in civil network planning to build the networks.
Application of Minimum Spanning Tree
Minimum Spanning Tree is widely used in real-life situations. Some of the applications of the Minimum Spanning Tree are as follows.
- Minimum Spanning Tree is used for designing telecommunication networks and water supply networks.
- For designing Local Area Networks.
- For solving the Traveling salesman problem
- Real-time face tracking and verification (i.e. locating human faces in a video stream).
- Minimum spanning trees can also be used to describe financial markets.
- Handwriting recognition of mathematical expressions.
- Curvilinear feature extraction in computer vision.
- For building or Connecting the roads among cities or villages at a minimal cost.
- Minimum Spanning Trees are used For clustering i.e. grouping of similar objects under one category and distinguishing from other categories.
Complexity Analysis
We have discussed two algorithms for constructing the minimum spanning tree. Let us have a look at the Time and Space complexity of these algorithms.
Kruskal's Algorithm
-
For the Adjacency Matrix representation of the graph.
Time Complexity: O(V2)
Space Complexity: O(V2)
In Kruskal's Algorithm, the time required for traversing the matrix is O(V2) so the overall time complexity is O(V2). Also to represent the matrix we use a 2-Dimensional array. So, we will require O(V2) space where V is the number of vertices in graph G.
-
For the Edge List representation of the graph.
Time Complexity: O(ElogE + ELogV)
Space Complexity: O(V + E)
Where E is the number of edges and V is the number of vertices in graph G.
Prim's Algorithm
-
For the Adjacency Matrix representation of the graph.
Time Complexity: O(V2)
Space Complexity: O(V2)
In Prim's Algorithm, the time required for traversing the matrix is O(V2) so the overall time complexity is O(V2). Also to represent the matrix we use a 2-Dimensional array. So, we will require O(V2) space where V is the number of vertices in graph G.
-
For the Adjacency List representation of the graph, Min Heap is used as time complexity of operations like extracting minimum element and decreasing key value is O(LogV) in Min Heap.
Time Complexity: O((V + E)logV)
Space Complexity: O(V + E)
Where E is the number of edges and V is the number of vertices in graph G.
Conclusion
- In this article, we have learned about the spanning tree and its interesting properties.
- We also learned about the Minimum Spanning tree and its properties.
- We saw various applications of Minimum Spanning Tree.
- Learned about what is clustering and How we can achieve clustering.
- Learned about the algorithms to construct a minimum spanning tree.
- Analysed the Time and Space Complexities of the minimum spanning tree algorithms.
Takeaways
The weight of a spanning tree is the sum of weights given to each edge of the spanning tree.

