Multivalued Dependency
Learn via video course

Overview
Multivalued dependency (MVD) states that two independent data variable rows say 'B' and 'C' in a table can be dependent on the third variable row 'A' respectively, i.e., for same value of attribute 'A', we can have multiple values of component 'B' and 'C'.
Scope of Article
In this article, we will discuss
- Significance of MVD.
- Representation of MVD.
- Condition for MVD to exist.
- Example of MVD, along with verification.
This article assumes that the reader has basic knowledge of DBMS.
Introduction
So, before we dive into the Multivalued Dependency of DBMS it’s a prerequisite that we should have a proper idea about how Data Base Management System works, for that you can refer to: “Data Base Management System” for better understanding.
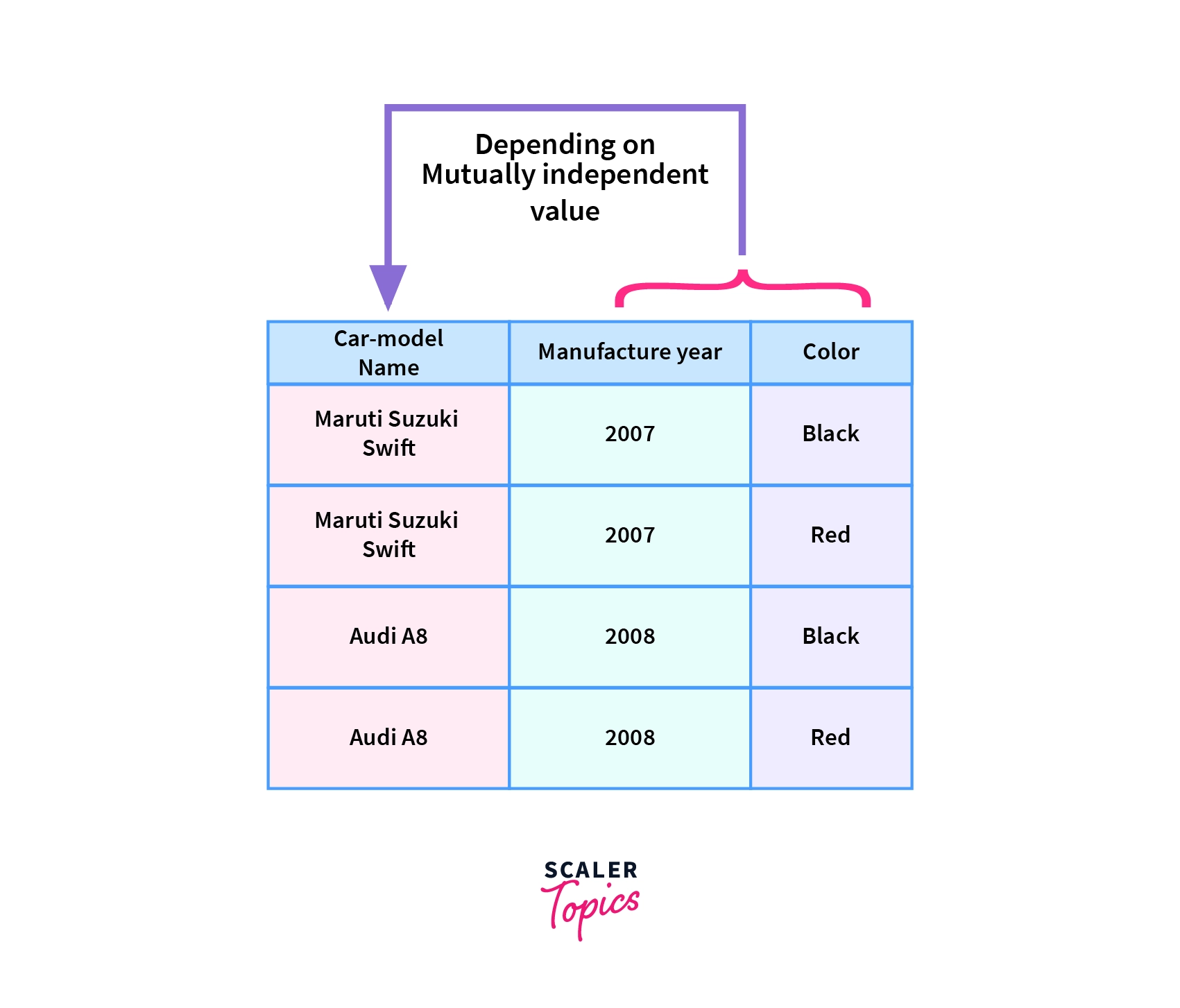
Occurrence of Multivalued Dependency(MVD)
- Multivalued Dependency occurs when two attributes in a table are independent of each other but are dependent on the third attribute.
- Since multivalued Dependency consists of a minimum of two variables (independent of each other) to be dependent on the third variable, so the minimum amount of variables required is two.
Representation of Multivalued Dependency(MVD)
we write MVD as,
a --> --> b
Which signifies for a single attribute 'a', there exist multiple values of 'b'.
The above expression is read as: 'a is multi-valued dependent on b'.
Condition For MVD
We can say multivalued dependency exists if all the following conditions are met.
If any attribute 'a' has multiple dependence on 'b', for any relation R, for all the pair data values in row R1 and row R2 in table, such that the relation
R1[a]=R2[a]
exists, and the relation between row R3 and row R4 exists in table, such that
R1[a] = R2[a] = R3[a] = R4[a]
R1[b] = R3[b], R2[b] = R4[b]
then we can say that Multivalued Dependency(MVD) exists.
Which means, in the Rows R1, R2, R3, and R4
- R1[a], R2[a], R3[a], R4[a] should contain the same value.
- The value of R1[b] should be equal to the value R3[b] and the value R2[b] should be equal to the value of R4[b].
Example of MVD
Now, let's make things clear by taking an example of MVD. Suppose a student named Rahul, who is taking courses on C++ and Python and has hobbies in Painting and Music.
| Row | Name | Course_work | Hobby |
|---|---|---|---|
| R1 | Rahul | C++ | Painting |
| R2 | Rahul | Python | Music |
| R3 | Rahul | C++ | Music |
| R4 | Rahul | Python | Painting |
Here Hobby and Course work are multivalued dependents on Name because for the same value of name "Rahul" we have different values of Project and Hobby.
Verification of Example
Now, let us check the condition of MVD on our table,
Condition 1 for MVD
R1[a] = R2[a] = R3[a] = R4[a]
Finding from the table,
R1[a] = R2[a] = R3[a] = R4[a] = 'Rahul'
Therefore, condition 1 seems to be satisfied.
Condition 2 for MVD
R1[b] = R3[b], R2[b] = R4[b]
Finding from the table,
R1[b] = R3[b] = 'C++', R2[b] = R4[b] = 'Python'
Therefore, condition 2 also seems to be satisfied.
Now coming to the last condition which is
Condition 3 for MVD
R1[c] = R4[c], R2[c] = R3[c]
Finding from the table, we can conclude
R1[c] = R4[c] = 'Painting', R2[c] = R3[c] = 'Music'
Therefore, condition 3 is also satisfied which means MVD exists in the given example.
So theoretically, we have
a --> --> b
And from the table, we got
Name --> --> Course work
And for,
a --> --> c
We have
Name --> --> Hobby
Finally, we can conclude in the given table with conditional relation as
Name --> --> Course Work
Name --> --> Hobby
Conclusion
Multivalued Dependency exists when the values two independent attributes, say b and c, are determined based on the third attribute a.
MVD is represented as 'a --> --> b'.
Therefore, we can say that for a multivalued dependency to exist in a relation R.
- Two components say B and C of a single attribute say A should be mutually independent of eachother.
- For two tuples of R, say A and B, for entire attributes of A, component B might have different values.
- Similarly, For two tuples of R, say A and C, for entire attributes of A the component C might have different values.
