Directed Graph in Data Structure
Learn via video course

Overview
A graph is a non-linear data structure. It consists of several nodes, also referred to as vertices. The nodes of a graph are connected through edges. A graph in which there's associated a sense of a specific direction with each edge is referred to as a directed graph. Directed graphs, from graph theory, are extensively used in solving mathematical problems, social media, applications, digital navigation, aerospace industry, etc.
Scope
In this article we shall discuss:
- What is a directed graph data structure.
- Common terminologies in Graphs.
- Implementation of a directed graph.
- How to traverse a directed graph.
- Example of the directed graph data structure.
What is a Directed Graph in Data Structure?
A directed graph is a data structure that stores data in vertices or nodes. These vertices may be connected and directed by edges. One vertex is directed towards another vertex through an edge between them.
The ordered pair, P = (V, A), where ‘V’ is a collection of nodes and ‘A’ is the collection of edges. We use these elements, i.e. nodes and edges, to make a directed graph data structure. Each edge in a directed graph has one particular direction. The direction of an edge between nodes 'n1' and 'n2' will either be from n1 to n2, or vice versa.
Graph Terminology
Path
A path from a node m to node n is a sequence of edges that can be traversed to start from m and reach n.
Simple path
If all the vertices in a path are distinct, then the path is referred to as a simple path.
Closed path
If the first vertex and the last vertex in a path are same, then the path is said to be closed.
Trail
A trail is an open path that does not have any repeated edges in it. The vertices in a trail may repeatedly occur, but all the edges in a trail are distinct.
Cycle
A non-empty path is called a cycle if it begins and ends at the same node.
Connected Graph
A graph is said to be connected if there exists a minimum of one path between every two distinct vertices.
Weighted Graph
It is a graph in which each edge is assigned a weight value. The weight of an edge may denote it's absolute importance, relative priority, length, etc.
Adjacent Nodes
In a graph, two nodes connected by an edge are called adjacent nodes or neighbors to one another.
Degree of the Node
The number of edges connected to a node is called the degree of the node. If a node is isolated then its degree is 0.
How a Graph is Implemented
There are 2 ways to implement graphs in a computer: 1. Adjacency matrix representation 2. Linked list representation
Adjacency Matrix Representation
In this representation, a matrix is used to store and hold the graph's data.
Adjacency Matrix for an Unweighted Directed Graph
Then size of the matrix used is N x N. Here, N is the number of nodes. The value at any position (i,j) in the matrix determines whether or not there exists an edge from ith node to jth node. Following is the diagram of a directed graph and its adjacency matrix .
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 1 | 0 | 1 | 0 |
| B | 0 | 0 | 1 | 0 | 0 |
| C | 0 | 0 | 0 | 1 | 0 |
| D | 0 | 0 | 0 | 0 | 1 |
| E | 1 | 0 | 0 | 0 | 0 |
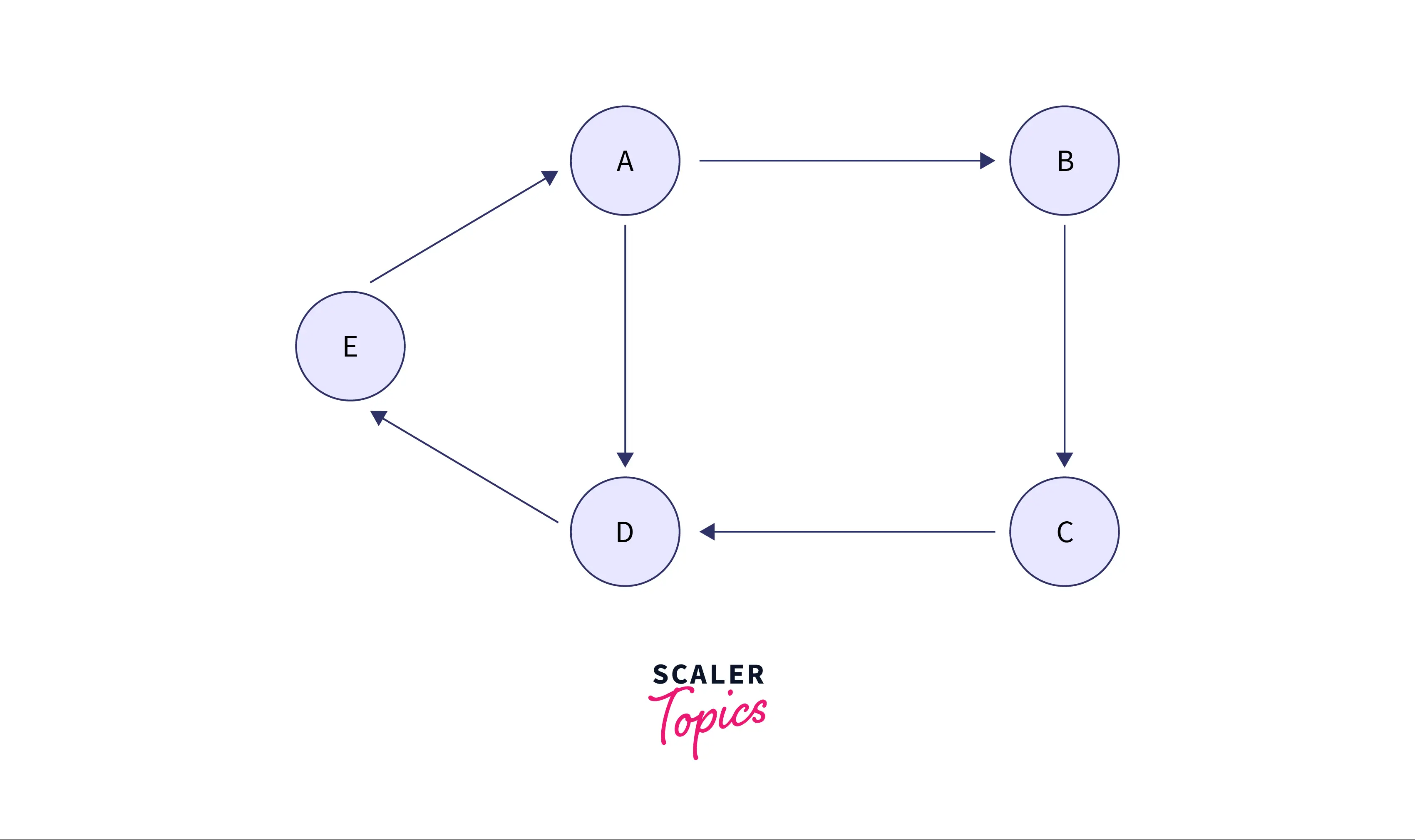
Adjacency Matrix for a Weighted Directed Graph
The matrix is similar to that of an unweighted graph. In order to accomodate the representation of the weight of edges, many techniques have been developed.
The most common technique is to fix one value for indicating the absence of an edge from node i to j. One suitable value is 0. Other values (1,2,3,... , -1,-2,-3...) may represent the presence of an edge as well as it's weight.
Adjacency List Representation
In this representation, an linked list is implemented to store and hold the graph’s data in the computer’s memory.
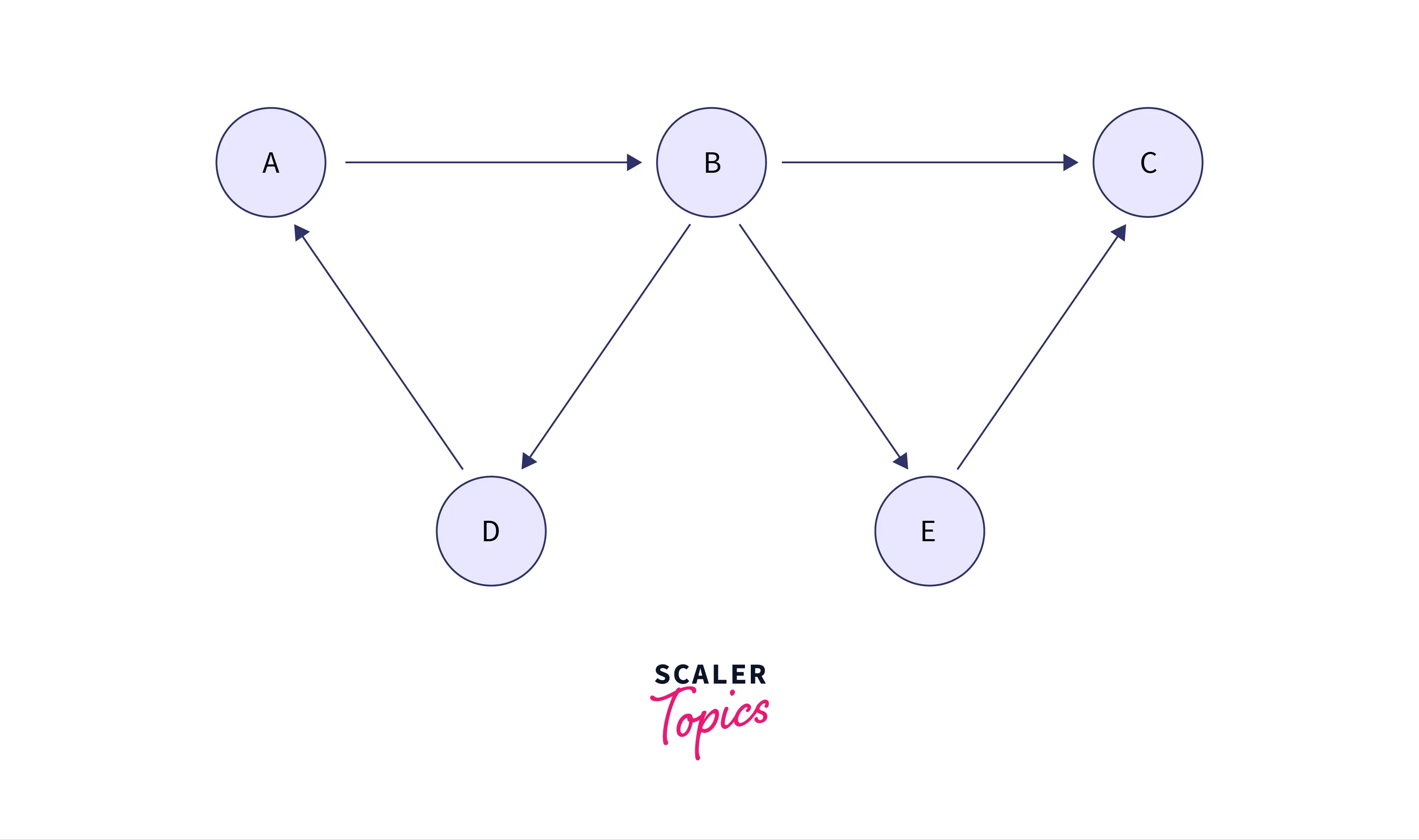
Adjacency List for an Unweighted Directed Graph
The diagram ahead shows a directed unweighted graph.
The diagram that follows is the adjacency list representation of the directed unweighted graph from diagram above.
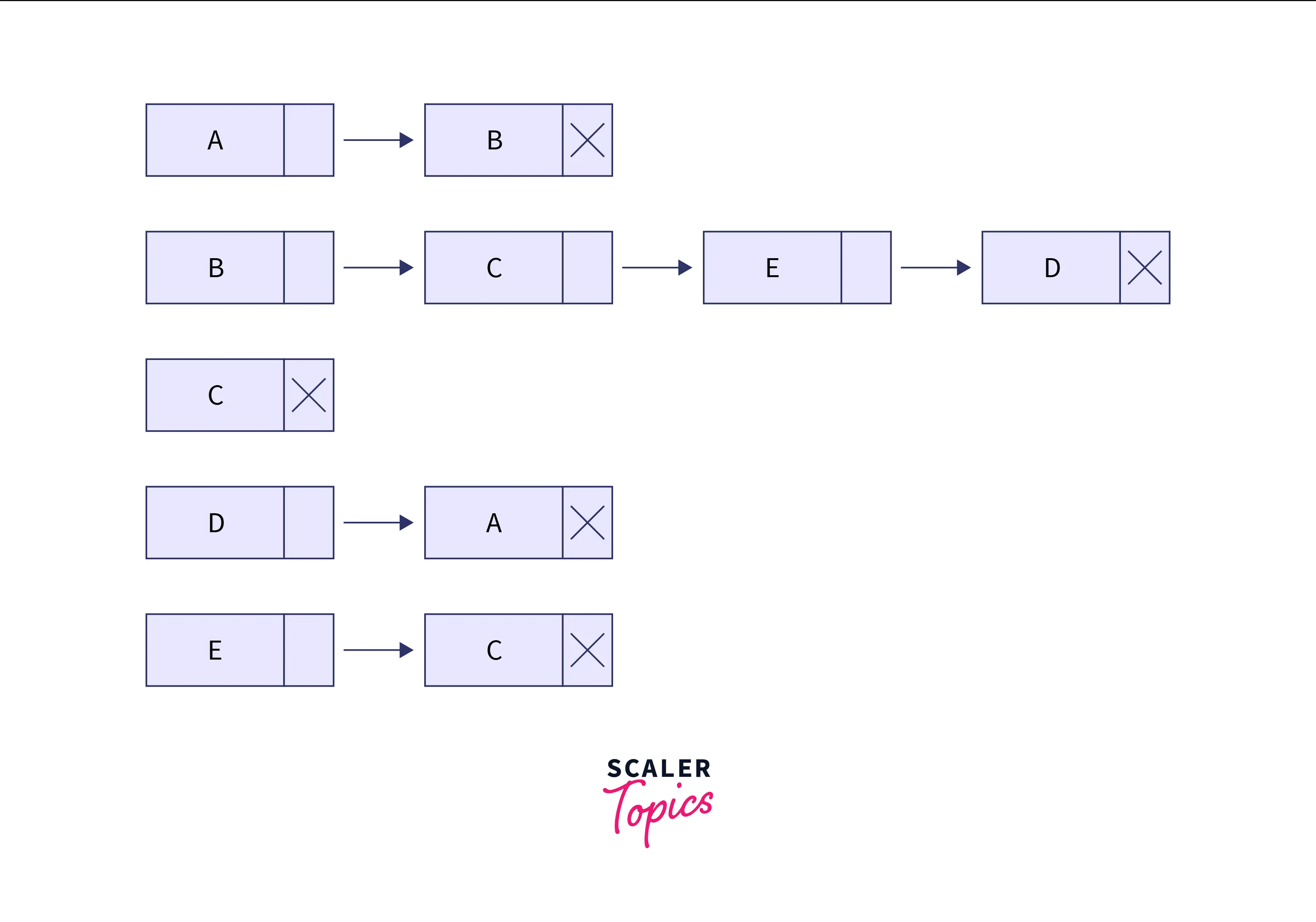
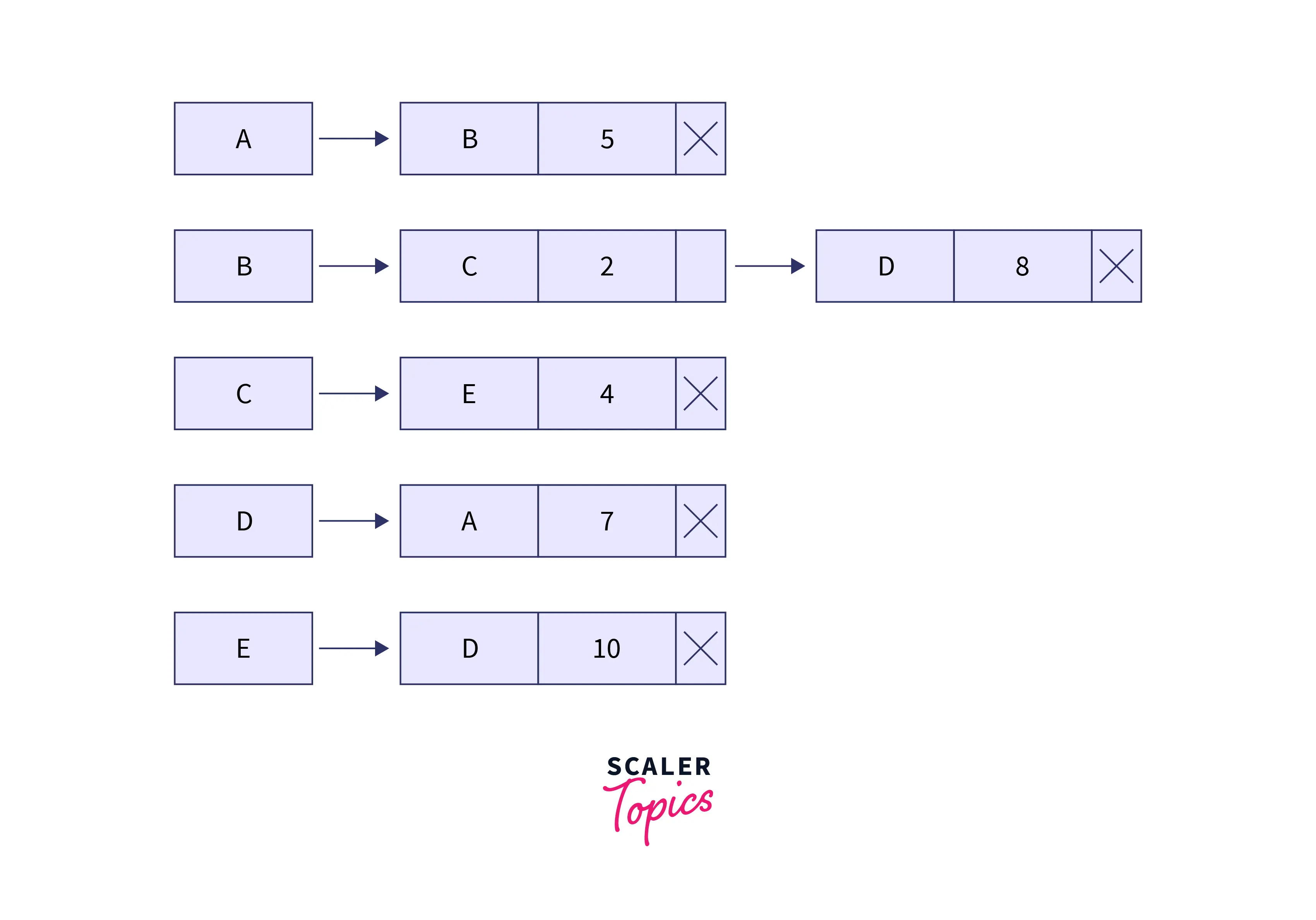
In the figure above, we can notice that for every vertex of the graph there is a node of a Linked list. The neighbors n1, n2, n3... of any edge i, are represented by a linked list mounted at i. This list contains all the neighbors n1, n2, n3... of i.
Adjacency List for a Weighted Graph
The adjacency list representation of a directed weighted graph is similar to that of an unweighted directed graph. Suppose there's a vertex i at which is mounted a list of it's neighbors v1, v2, v3... The linked list node of the jth neignbor of i, vj will contain the following 3 items:
- The value of the neighbor vertex v[j].
- The weight of the edge from current graph vertex i to the neighbor j.
- A pointer that points to the linked list node of the next neighbor graph vertex (v[j+1]). If there does not exist any further neighboring graph vertices, the next pointer points to null.
The following diagram shows a directed weighted graph.
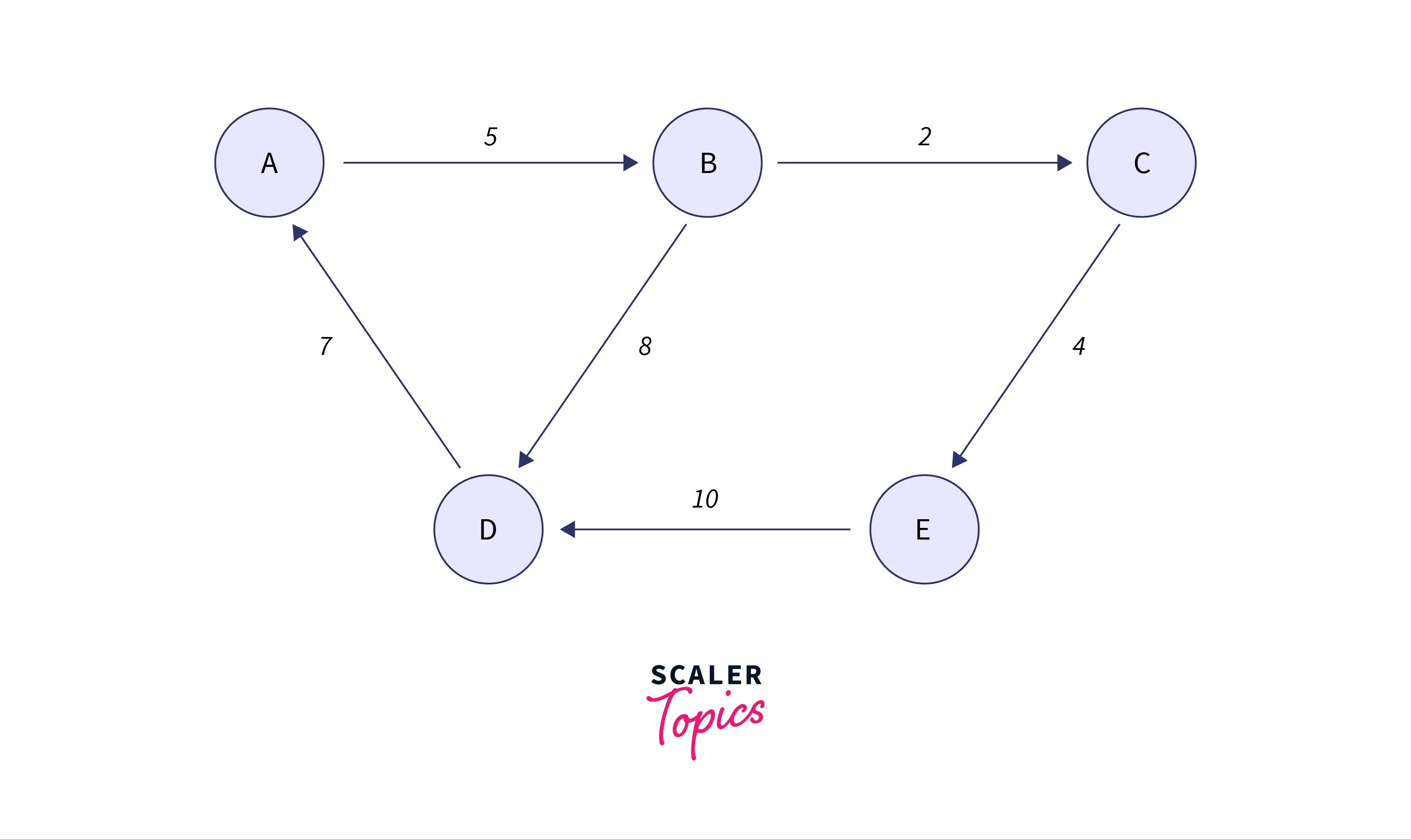
The following diagram shows the adjacency list representation of the above shown graph.
How to Traverse the Directed Graph
There are two ways of traversing a directed graph:
- BFS (Breadth First Search)
- DFS (Depth First Search)
BFS
BFS (Breadth First Search) is a traversal algorithm designed to traverse a graph, initiating from the root node of the graph and exploring all the other neighboring nodes. Then the process is repeated for all the neighbors.
In the graph, any given node can be selected as the root node while implementing the BFS. The state of any vertex during the traversal is either visited or unvisited. A node is marked visited once it is explored. A node that is marked visited is not traversed further. This helps in dealing with loops and cycles.
Algorithm
The steps of the algorithm for the BFS are as follows-
- Make a FIFO (Fisrt In First Out) queue and push the root. in it.
- Mark the root visited.
- Repeat the following steps while the queue is not empty:
- Pop an item out from the queue, process it.
- Mark all of its unvisited neighbors as visited and push them in the queue.
- END
Complexity of BFS Algorithm
The time complexity of BFS is O(n) where n is the number of nodes. Because we are exploring each node in the graph exactly once.
The space complexity of BFS is also O(n), as at a time the maximum number of nodes present in the queue can be upto n- the total number of nodes in the graph.
DFS
DFS (Depth First Search) is a recursive approach implemented to traverse a graph. It is implemented to visit all the vertices of the graph or the tree with the initial node and goes deeper and deeper until the targetted node or a node with no children (called leaf node) is found. The stack data structure can be used to implement the DFS algorithm due to its recursive nature.
Algorithm
Following are the steps involved in doing a DFS traversal of a directed graph:
- Make a LIFO (Last In First Out) stack and push the root in it.
- Mark the root visited.
- Repeat the following steps while the stack is not empty:
- Pop out an item from the stack.
- Mark all of its unvisited neighbors as visited and push them in the stack.
- END.
Complexity of Depth-first Search Algorithm
The time complexity of DFS is O(n) where n is the number of nodes. Because we are exploring each node in the graph exactly once.
The space complexity of DFS is also O(n), as at a time the maximum number of nodes present in the stack can be upto n- the total number of nodes in the graph.
Example for Directed Graph in Data Structure
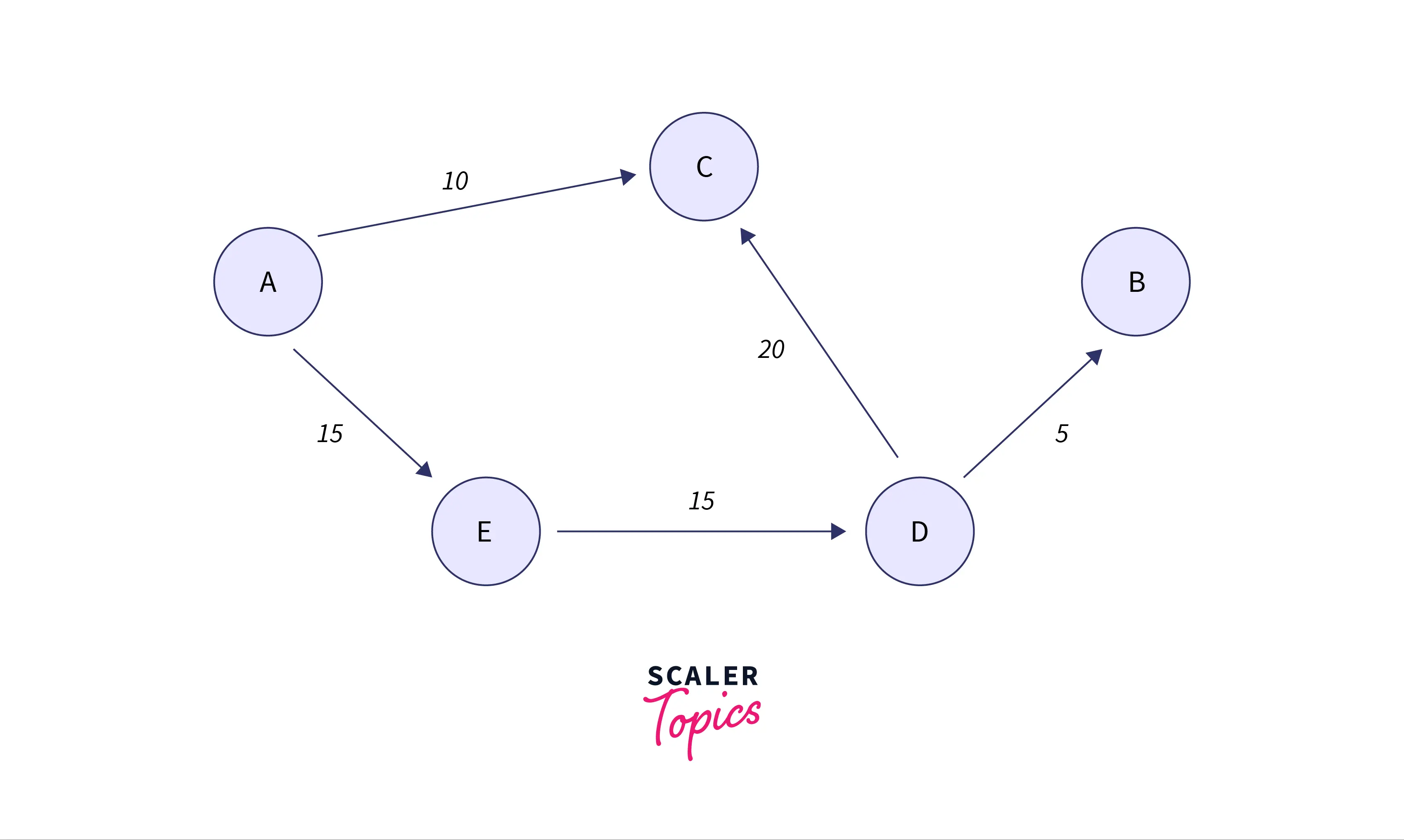
A simple example of a directed graph can be considered as a matrix A containing the edges between 5 different vertices (A,B,C,D, and E).
| A | B | C | D | E | |
|---|---|---|---|---|---|
| A | 0 | 0 | 10 | 0 | 15 |
| B | 0 | 0 | 0 | 0 | 0 |
| C | 0 | 0 | 0 | 0 | 0 |
| D | 0 | 5 | 20 | 0 | 0 |
| E | 0 | 0 | 0 | 15 | 0 |
Now from the above matrix, a graph can be constructed with the edges directed from row to column.
If for a particular cell, there is 0, then it means there is no edge between that cell's row and the cell's column. Also, other than 0 if there is an integer then it means that there is an edge between that cell's row and column also the number in that cell is the weight of the edge.
Conclusion
- A directed graph is a data structure that stores data in vertices or nodes and these nodes or vertices are connected and also directed by edges (one vertex is directed towards another vertex through an edge) that may have some weight.
- Directed graph is also called a digraph or directed network.
- The number of edges that a node is connected to is called its degree. If a node is isolated then its degree is 0.
- In matrix representation, an adjacency matrix is used to store and hold the graph.
- In list representation, an adjacency linked-list is implemented to store and hold the graphs data in the computer’s memory.
- In an adjacency list, because of the implementation of a linked list, it becomes very easy to add a vertex.
- There are two ways with which you can traverse in a graph: BFS and DFS.
- Time complexity of BFS is dependent on the data structure used to implement the graph. The complexity of BFS is O(V+E).
- DFS (Depth First Search) is a recursive approach implemented to traverse a graph.
- The stack data structure is used to implement the DFS algorithm due to its recursive nature.
- DFS algorithm’s time complexity is also O(V+E), where the number of edges is E and the number of vertices in V.
