Program to Implement Insertion Sort in C++

Introduction to Insertion Sort

Insertion sort is a sorting algorithm that is used to place elements of an array in their correct position. To Sort elements using the insertion sort algorithm, we divide an array into two parts where the first part is the sorted part and the second one is the unsorted part. We consider first index of the array as sorted and then we will compare it with its adjacent element means the element on the right side. If the adjacent element is less than the sorted one then they will be swapped which means the element will be placed on the left side or else it will be placed on the right side. This particular process will be repeated until the entire array becomes sorted. In short words, insertion sort works by comparing each element with the previous element and then placing them accordingly.

Insertion sort can be applied where the size of an array is less because it is inefficient for larger data sets.

Insertion sort has several advantages as it has a simple implementation compared to other sorting algorithms. It is adaptable as it is a preferred sorting algorithm for data that is significantly sorted.

Insertion sort is an efficient algorithm when compared to other sorting algorithms like selection sort and bubble sort but it is less efficient than sorting algorithms like Quicksort, Merge sort, and Heapsort.

Working of the Insertion Sort algorithm in C++

Now, let's know about the working of the insertion sort C++ algorithm and how it behaves in every iteration.

Let's suppose we have an array to be sorted as given below:

First Pass

In the above array, we will consider the first element as already sorted. Therefore, the first element is considered sorted. The remaining array will be considered unsorted.

Second Pass

Now, we will iterate through the entire elements of the array and then compare them with their previous element. We will compare the second element with the first element and if it is smaller than the first element, the second element will be placed in place of the first element.

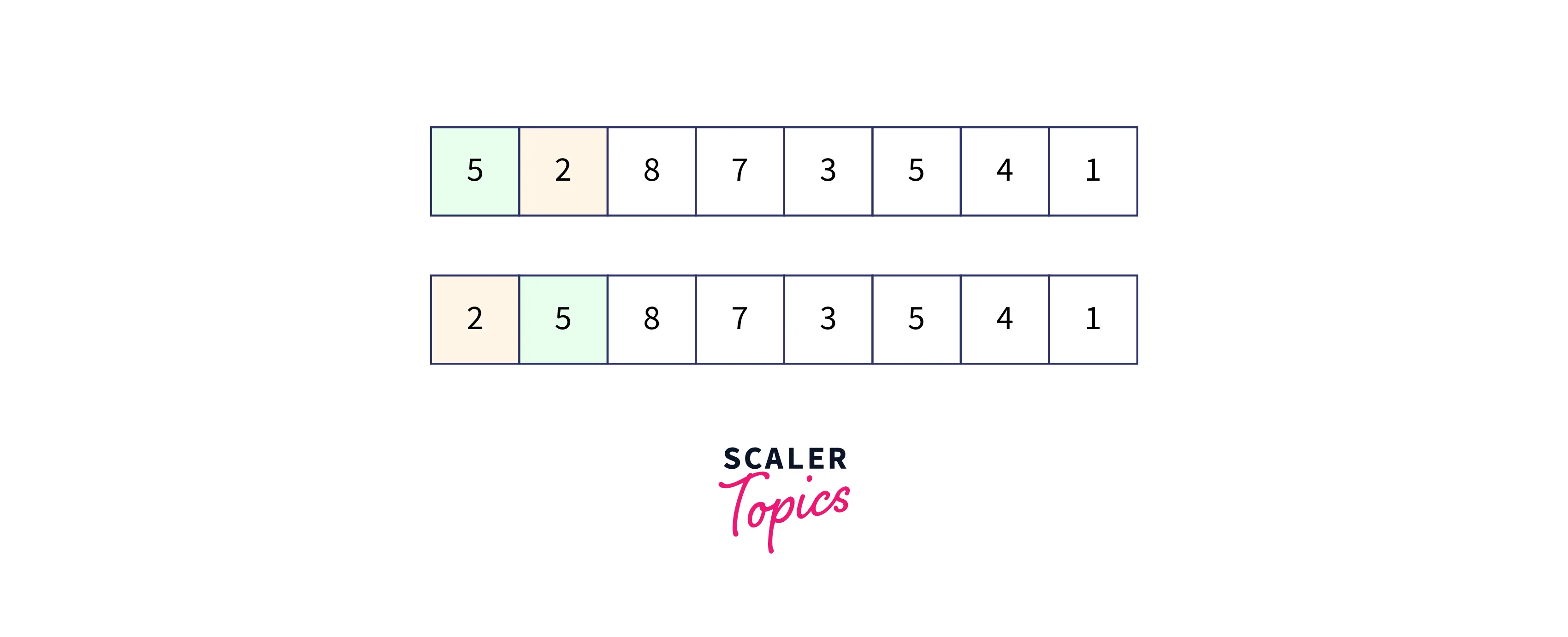
Third Pass

After sorting the first two elements, if the next value in the array is more or greater than the previous element, then the next element's place remains unchanged, which means no swapping will happen.

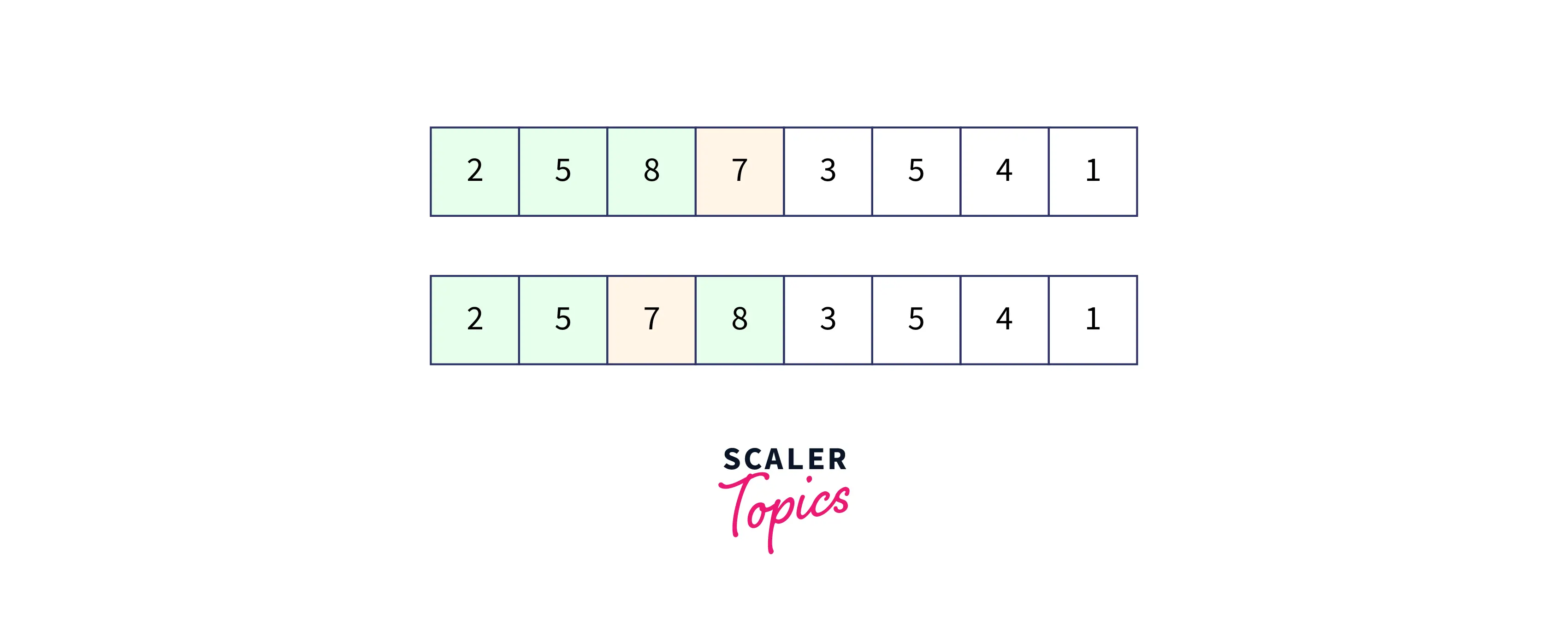
Fourth Pass

Similarly, we will place every element which is unsorted in its correct position so that they will be sorted.

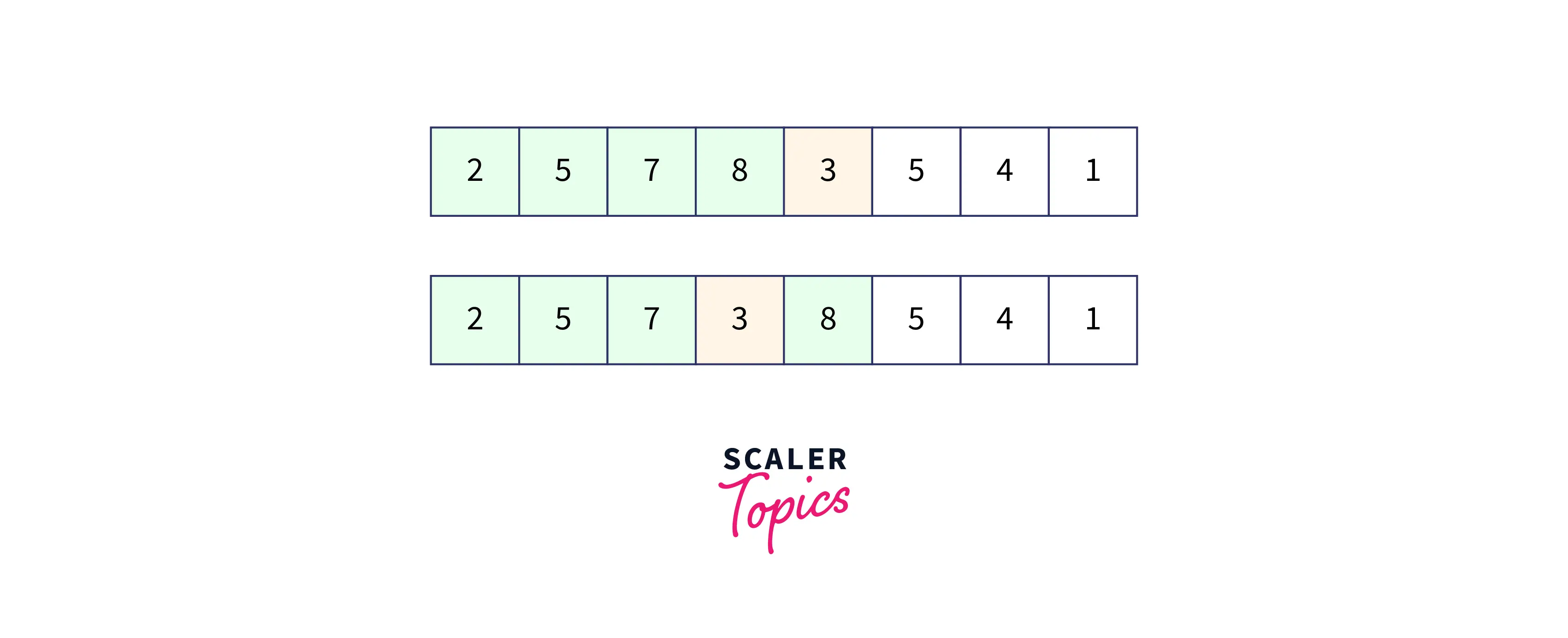
• Here, in the above, we are comparing the element until it becomes sorted and placed at its correct position by comparing it with its adjacent element.

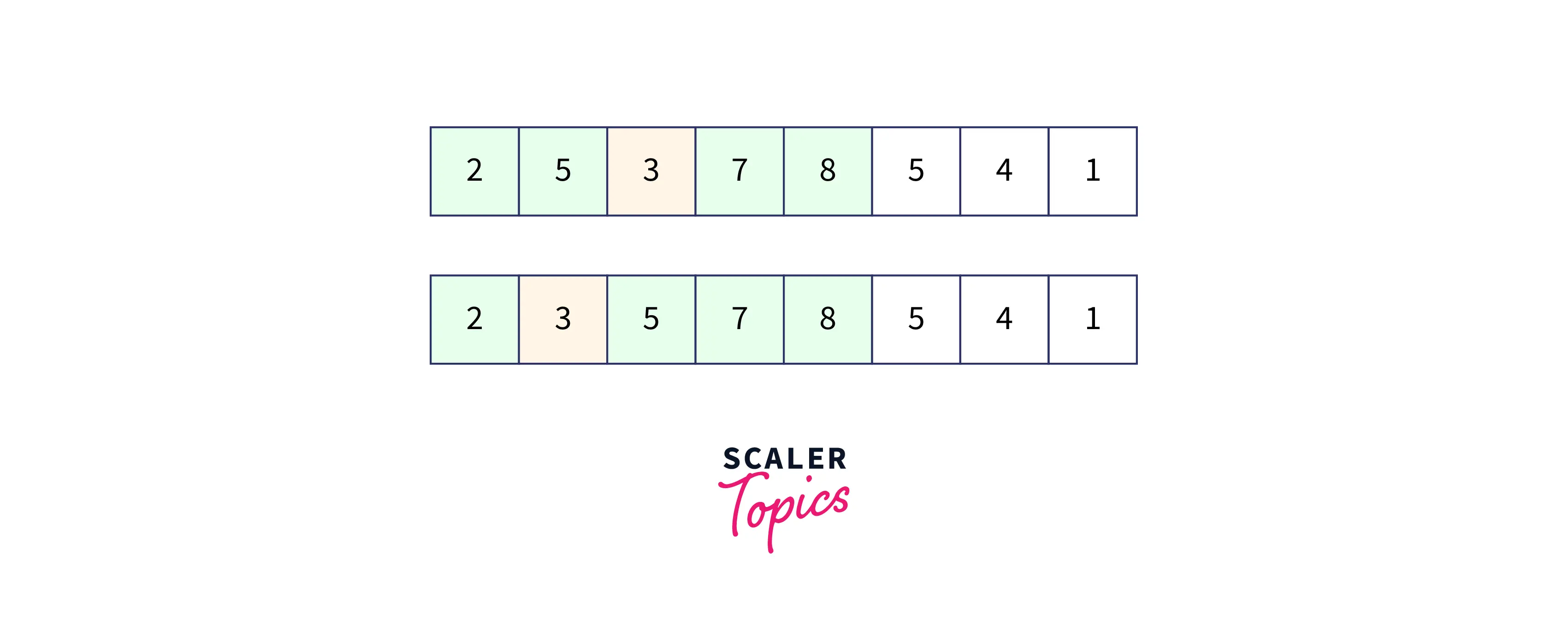
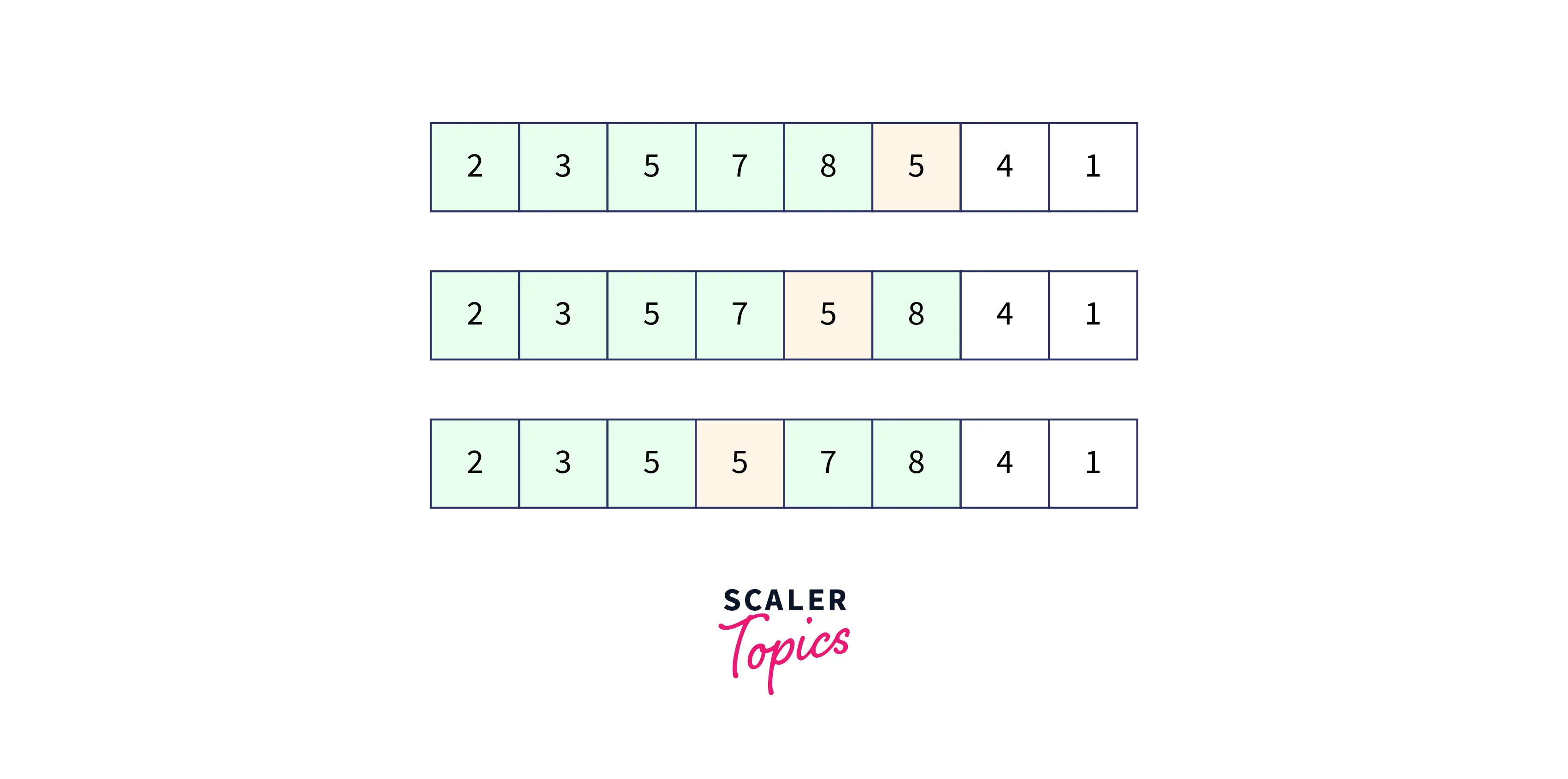
• In the above image, we have repeated the previous steps and keep changing the position of 5 until it becomes sorted.
• We will keep repeating the steps discussed earlier and that's how we will get our sorted array as seen in the image below:

Insertion Sort Algorithm in C++

After having a detailed explanation about the introduction and working of insertion sort C++. Now, let's discuss the algorithm used for its implementation.

Algorithm

Let's now discuss the implementation of insertion sort.

Code

Output

Explanation: In the above program, we have initialized an array array with its elements. After that, we initialized a variable named size with shows the size of the given array. From the main method, we have called the insertionSort() method which will sort the array passed as an argument.

In the insertionSort() method, we have two for loops in which the first is used to select elements and the second is used to compare the previouly sorted element with the selected element. Inside the inner for loop, we have an if statement which specifies whether the current element var is less than the sorted element arr[j], and if yes, then they are interchanged. Else, we will get out of the loop using the break statement and the current element will be placed at the start index or the element which is considered as sorted. This process will continue until the entire array becomes sorted. After sorting, we printed the sorted array using a for loop.

Insertion Sort in C++ Complexity

Now, let's discuss the efficiency of the insertion sort C++ algorithm which is done by analyzing the complexity of the algorithm which is both Time (Best, Worst, and Average) and Space complexity.

Time Complexity

The time complexity of the insertion sort algorithm comes out to be O(n^2) according to the comparisons required to sort the entire element of the array as we compare adjacent elements so We require two loops that may go from 1 to n, and therefore time complexity becomes O(n^2).

Best Case Complexity

The Best case complexity occurs in insertion sort when the given array or list is already sorted. In this particular case, only the outer loop runs for n times. Therefore, the complexity comes out to be linear that is O(n).

Worst Case Complexity

The Worst case complexity occurs in insertion sort when the given array has to be sorted in ascending order and it is already sorted in descending order. Each element of the array will be compared with every other element. We have to make (n-1) comparisons for every nth element. Therefore, the complexity comes out to be O(n^2)

Average Case Complexity

The Average case complexity occurs in the situation when the elements of the array or list are randomly arranged rather than in ascending or descending order. Hence, the average case time complexity comes out to be O(n^2).

Space Complexity

The Space Complexity of the insertion sort C++ algorithm comes out to be O(1) which is Constant Space as there is no extra space or data structure used in the algorithm other than the temporary variables.

Characteristics of Insertion Sort in C++

Now, after discussing the efficiency of the insertion sort algorithm, let's now take at some of the important characteristics of insertion sort.

• Insertion sort algorithm is an adaptive algorithm. Here, adaptive refers to the fewer number of steps taken by insertion sort to sort an array when that array is somewhat sorted.

• The best case algorithm is efficient when compared to algorithms like selection sort and bubble sort.

• The overall space complexity of insertion sort is constant that is O(1) which means this algorithm does not take any extra space other than temporary variables used to store values.

• Insertion sort is not preferable or efficient for an array or lists having more elements rather it is an efficient algorithm for small arrays or small data sets.

• Is Insertion Sort a stable algorithm? Answer- Yes, insertion sort is a stable algorithm as it preserves the order relatively with equal values.

Insertion Sort Applications

Let's take a look at some of the applications of insertion sort as to where this algorithm can be used efficiently as compared to other sorting algorithms.

• Insertion sort can be used where the size of the data set is smaller or the size of an array or list is smaller.
• Insertion sort algorithm can be used where the given array is already partially sorted and few of the elements are still left to be sorted.

FAQs regarding Insertion Sort:

Let's take a look at some of the frequently asked questions related to insertion sort C++.

• Q1. What is the algorithmic paradigm of Insertion Sort? Answer: Insertion sort algorithm uses an incremental algorithmic approach to sort elements.

• Q2. When is Insertion sort generally used? Answer: Insertion sort algorithm is generally used where the size of the data set is smaller or the size of an array or list is smaller. It can be used where the given array is already partially sorted.