Insertion Sort Program in C

Insertion Sort

Insertion Sort is one of the simple sorting algorithms used to sort the array. Say we have two boxes, box1 and box2. box1 contains items in random order and box2 is empty. Now we pick each item from box1 and place this item in box2 such that the items in box2 are in sorted order after each addition.

This can be done by assuming the first element inserted is in its right position and from the next element, its right position is searched and the element at that position as well as elements placed after it is moved one step forward so that the current element is placed at right position and items are in sorted order.

The same procedure is applied to the array as well. Instead of using two arrays, the given array is divided into two parts i.e. the sorted one and the unsorted one. Values from the unsorted section are picked one by one and placed in the sorted part at their right position.

Characteristics of Insertion Sort

• It is one of the simplest algorithms to sort an array. It is easy to understand and implement.
• It is efficient only for a small number of data values.
• Insertion sort is appropriate if the data is partially sorted i.e. it is adaptive in nature.
• It follows an incremental approach i.e. the number of elements in the sorted section of the array is increased one by one.
• It is a stable and in-place sorting algorithm.

Algorithm

The steps to implement the insertion sort algorithm are described below:

1. We assume that the array is empty and on inserting one element into it will not affect the sorting order of the array. Thus, the first element is already sorted.
2. We run a loop from the second element to the last element in the array. In each iteration, the current element is compared with the previous elements, and its correct position is searched.
3. If the current element is greater than or equal to the previous element then we simply move toward the next iteration. If the current element is smaller than previous elements all the elements greater than the current are shifted one position to the right and the current element is placed at its correct position.
4. Step 3 is repeated for each element in the array.

The array is sorted now. Let us look at its pseudo code for a better understanding:

In the above code, the outer for loop visits each element of the array. The inner while loop moves all the elements greater than cur to the one position right. At last, the cur is placed in its right position.

Working of Insertion Sort Algorithm

Let us take an example of the array as follows: {45, 33, 2, 60, 71, 68} Initially, the array is as follows:

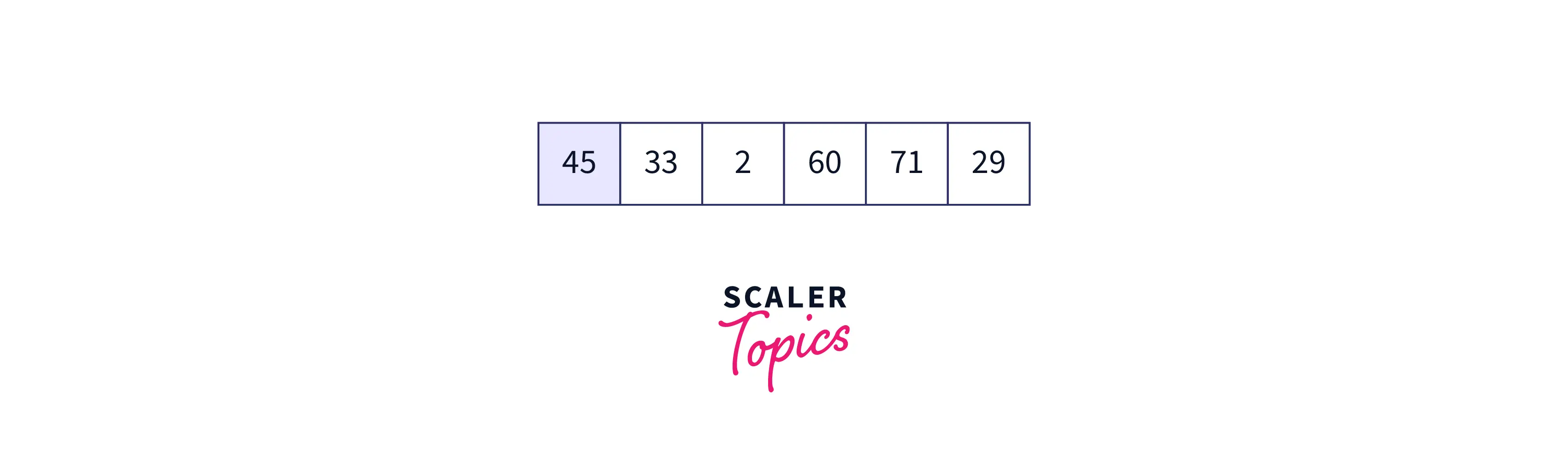
First iteration:

• Initially, the first element is sorted, i points to the second element i.e. 33. Now j points to the 45. After running the while loop, j = -1, cur = 33, and the array is -

While Loop:

• At the end of for loops iteration we place cur at its position i.e. j+1 = 0 and the array becomes

Second iteration:

• Now I point to 2 and j points to 33. After execution of the while loop

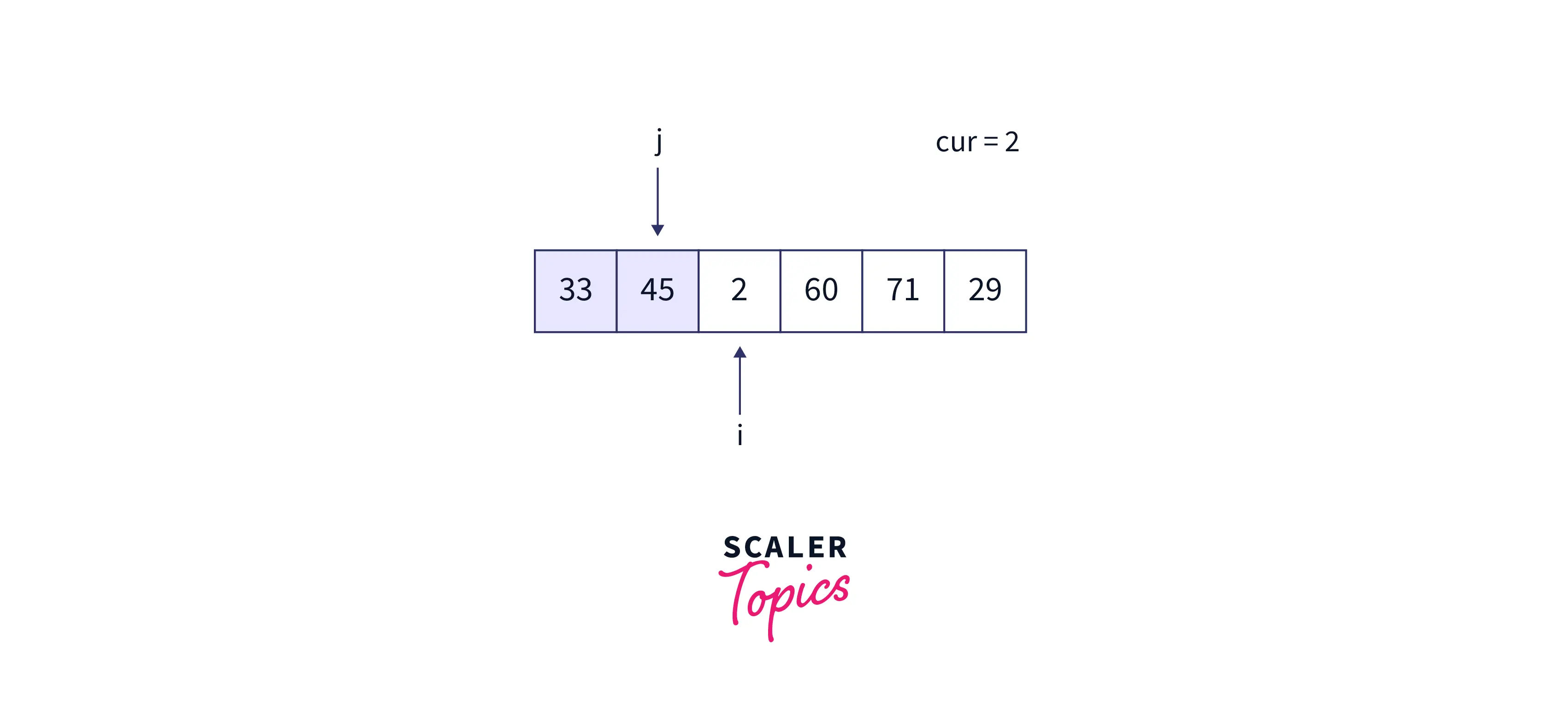
While Loop:

• arr[j] = cur

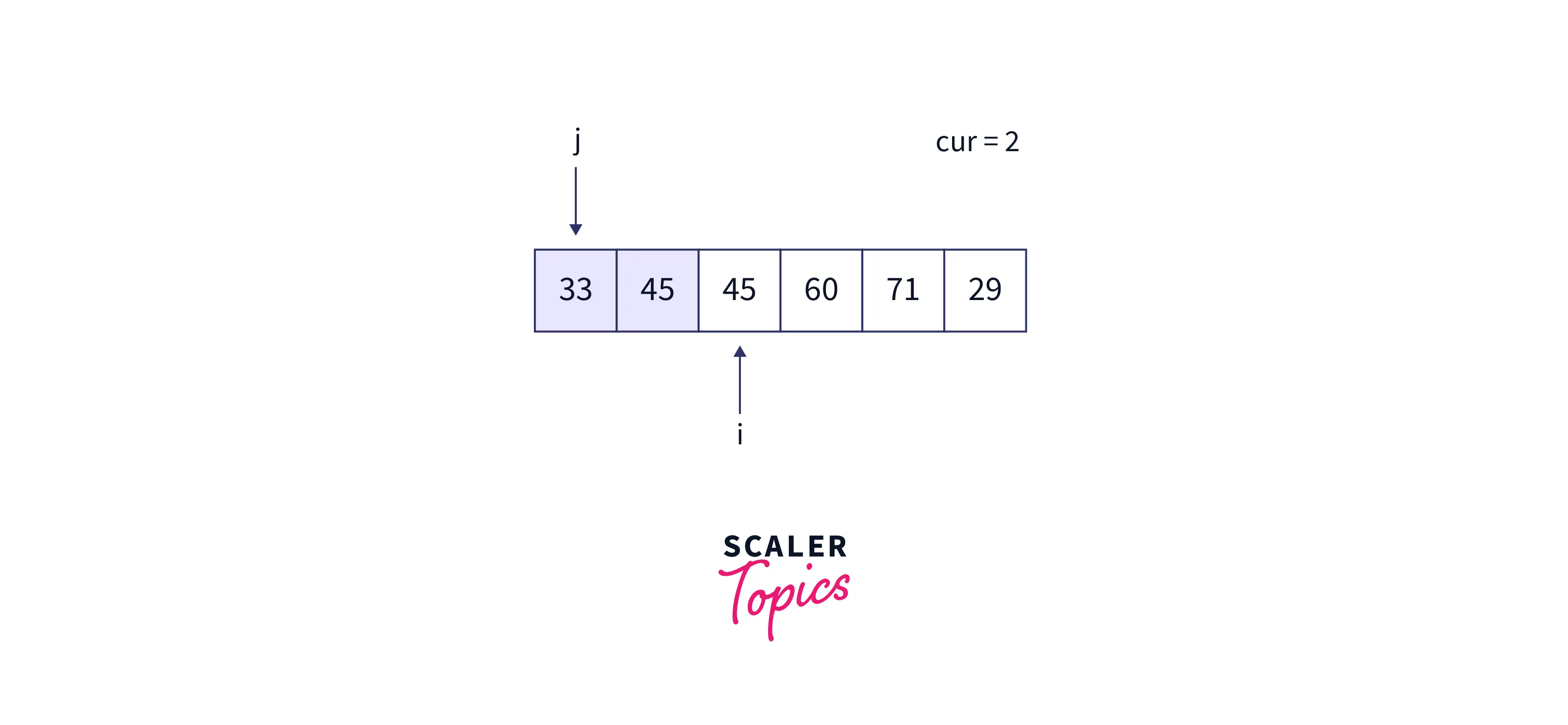
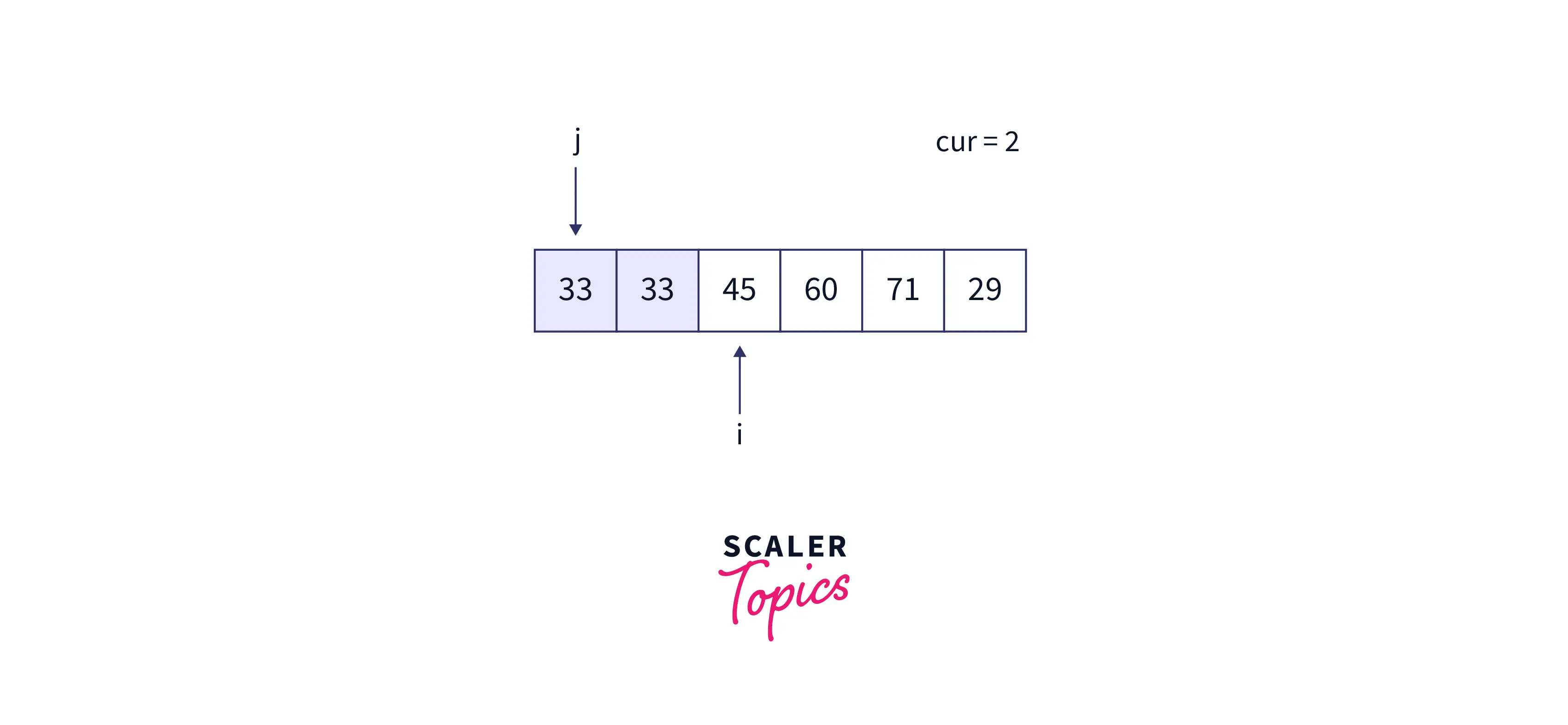
At the end of the second iteration, the array is as follows:

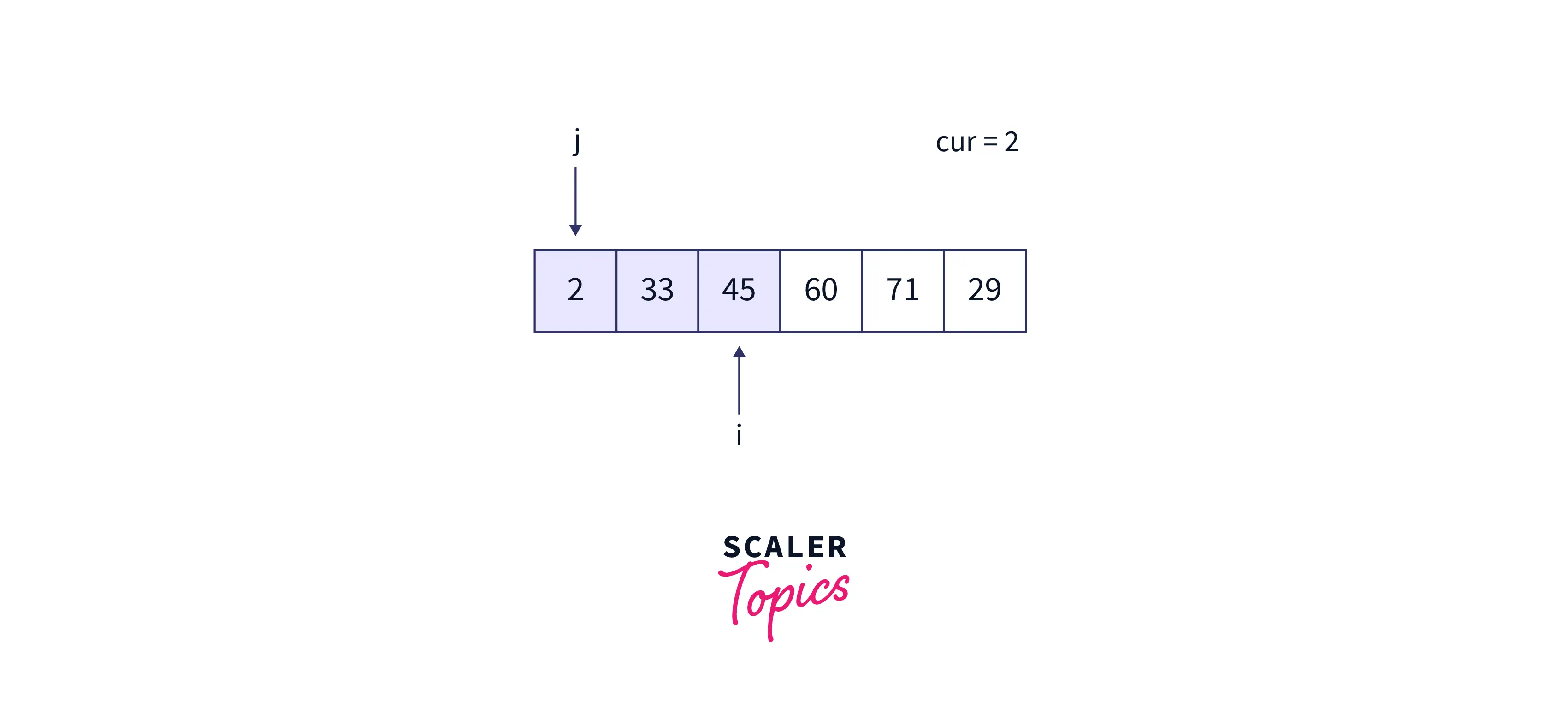
Third iteration: At the beginning of the third iteration,

• cur = 60, j points to 45, 60 is greater than 45 and thus, we are not required to modify anything in this iteration.

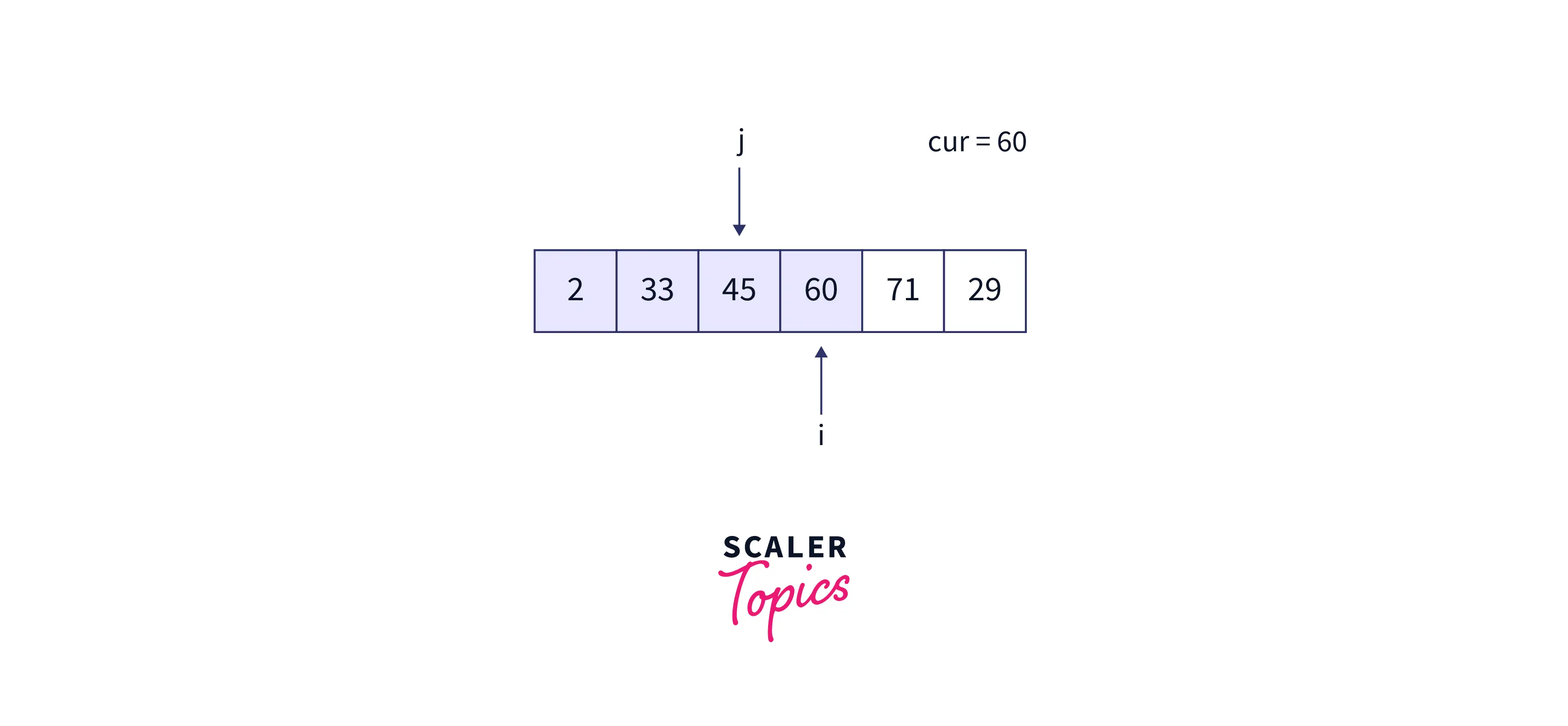
Fourth iteration:

• At the beginning of the fourth iteration,

• Now, cur = 71, j is 60 which is less than 71. Thus, again the array is sorted so far.

Fifth iteration:

• Array at the beginning of the fifth iteration:

• Lastly, i points to 29 i.e. cur = 29 and j = 4 i.e. 71. Variation during the while loop in the array is as follows:

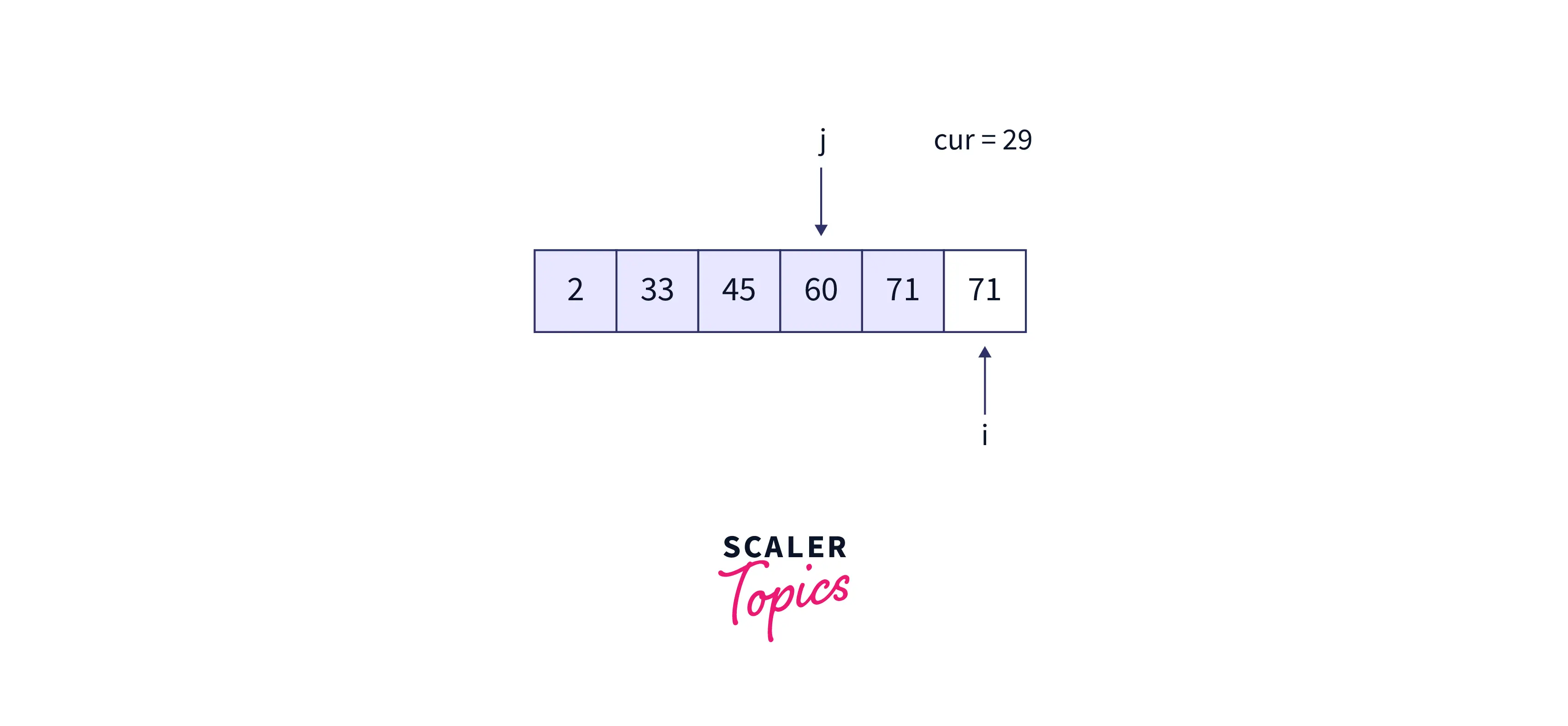
• Now cur must be placed at position 4. The resultant array is as follows:

The sorted array after execution of the insertion sort is as follows:

Implementation of Insertion Sort

C Program for Insertion Sort using For Loop

The simplest approach to implementing the insertion sort program in C is given below. We are using an outer loop to visit all the elements of the loop and an inner while loop to search for the position of the current element and shift greater elements to one step right.

Output:

Insertion Sort Program in C using While Loop

Another way to implement the insertion sort program in C is using two while loops i.e. a while loop inside the while loop. It is the same as the above implementation. The only variation is we are using a while loop to traverse the array instead of for loop.

Output:

Insertion Sort in C Using Functions

Let us see another way to implement the insertion sort program in C. In this example, we are using the swap function to move all the elements to the right. It makes the code more readable and easy to understand. The first for loop is used to traverse the array. The second for loop is used to find the right position for the current element and shift all the previous greater elements to the right side. As we are swapping the current element we are not required to place the element at its position in the end.

Output:

Insertion Sort Complexity

Time Complexity

The time complexity for the Insertion sort Program in C is given below:

• Best Case - The best case is when all the elements of the array are sorted and we simply run the outer for loop whose time complexity is O(n). Thus, in the best case time complexity of the insertion sort is O(n).
• Worst Case - In the worst case all the elements are in reverse order i.e. suppose we have to sort the array in ascending order. Still, it is in descending order, and thus along with outer for loop, inner while loop runs for O(n) time for each element in the outer loop. This is the worst case and the time complexity for the same is $O(n^2)$. It will consume the maximum amount of time to sort such an array.
• Average Case - It is the case when the elements are in jumbled order, i.e. it is not strictly in ascending or descending order. The average time complexity for this case is $O(n^2)$ as the inner while loop has to be iterated for each element of the array until its correct position is found.

Space Complexity

• As we are swapping elements rather than using another array for sorting purposes so no extra space is occupied and thus, the space complexity of the insertion sort program in C is O(1).

Advantages and Disadvantages of An Insertion Sort Algorithm

Advantages

• Insertion sort program in C is simple and easy to implement.
• It is an efficient sorting algorithm for small data sets.
• It doesn't use any extra space.
• If data is almost sorted then insertion sort is very fast approaching.

Disadvantages

• Its time complexity for the average and worst case is $O(n^2)$.
• It is not convenient for large data sets to have elements in random order.