Merge Sort Program in C

Introduction to Merge Sort in C

Merge sort is a sorting technique based on divide and conquer technique. In Merge sort, we divide the array recursively in two halves, until each sub-array contains a single element, and then we merge the sub-array in a way that it results into a sorted array. merge() function merges two sorted sub-arrays into one, wherein it assumes that array[l .. n] and arr[n+1 .. r] are sorted.

Algorithm of Merge Sort in C

How to Implement Merge Sort in C?

• Merge Sort Function in C

The following is the code implementation of the merge_sort function. In this function, we will find the mid-point, and then we will call the merge_sort function for array elements from left to mid-point and from index next to mid-point to rightmost index. Then we will call the merge function to merge the array.

Code:

Explanation of the code:

The function will first calculate the mid value using l + (right - left) / 2 then it will recursively call the mergesort function for values from left to mid and mid+1 to right respectively. It will call the merge function at the end to merge the portion ranging from left to right.

The base case: The merge_sort function will work until we have an array of unit sizes, this will operate only until the (left < right) condition holds true since for an array of unit sizes the value of left will be equal to the value of right.

• Merge Function in C

The following is the code implementation of the merge_sort function. The merge function is used to merge two subarrays of arr[], arr[left..mid] and arr[mid+1..right]. For this, two arrays left_arr and right_arr are created to store items in the range left to mid and mid+1 to right respectively.

Code:

Explanation of the code:

In the above merge function we are taking an array and left, mid, and right values as parameters. It will merge two subarrays of arr[], the first subarray is arr[left..mid] and the second subarray is arr[mid+1..right]. Now we will create two arrays left_arr and right_arr and store items in the range left to mid and mid+1 to right respectively.

After that, we will iterate through the arr and assign the values from the left_arr and right_arr accordingly.

How Merge Sort Works in C?

• To divide the given array of size N and divide it into two halves of size N/2, then take each half and divide them into halves. Keep doing it until the whole array is divided into N subarrays.
• Now take the adjacent pair of array items and merge them in a way that the merged array is sorted.
• Keep repeating the second step until the complete array of size N is formed.

Let us consider an array [6, 8, 2, 4, 1, 3]. As we can we that the given array is not sorted. We can apply a merge sort algorithm to sort this array.

The following picture depicts the merge sort operation on the array:

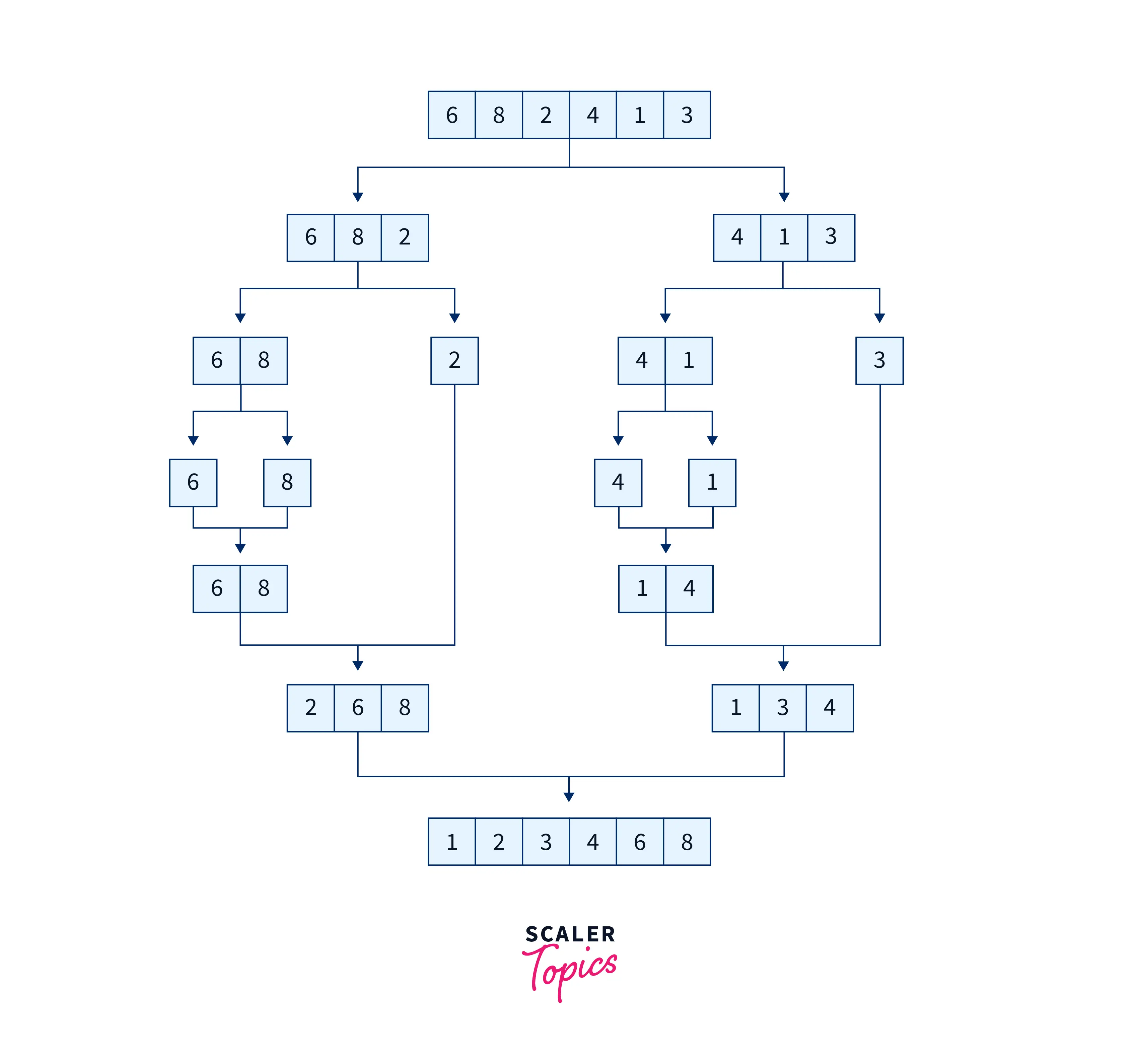
The whole process can be divided into two steps:

• Step 1: Dividing the array into two halves.

In this step, we are dividing the given array into two halves. Here the size of the array [6, 8, 2, 4, 1, 3] is 6 thus the value of mid will be (size of the array)/2 which equals 3.

The array will be divided into two arrays ranging from index[0, 3] (i.e. 0 to mid-1) and index[3, 5]. Now we have two arrays [6, 8, 2] and [4, 1, 3] each of size 3.

Now again, we will follow the above step to divide the two arrays [6, 8, 2] and [4, 1, 3] into two halves, respectively. In both cases, the size of the array is 3; thus the value of mid will be 3/2, which equals 1 (The value will be 1.5 but the ceil value is taken becindex[0, 1]ause the array indexes are integers). Now we will divide both the array into two haves of size 2 and 1, respectively. Thus we will have two arrays [6, 8] and [2] for the array [6, 8, 2] and [4, 1] and [3] for the array [4, 1, 3].

We will keep repeating this step until we have an array of unit sizes.

• Step 2: Merging the arrays.

Now that we have individual arrays of unit size, the arrays will be merged in a manner that the items in the merged array at every step are in sorted order. The merging of arrays will occur in the opposite order of the way the arrays were divided, i.e. firstly the unit arrays will be merged into the size of 2, then the arrays of the size of two will be merged into the size of 4 and so on and eventually we will have two halves of the original array which will together be merged into one sorted array.

In the first step the arrays [6] and [8] will be merged into array [6, 8]. Now the unit array [2] will be merged with the array [6, 8] and end up in an array [2, 6, 8]. Similarly the arrays [4] and [1] will be merged into the array [1, 4] and the arrays [1, 4] and [3] will merge into [1, 3, 4].

Now in the final step, we will merge [2, 6, 8] and [1, 3, 4] such that it stores items in a sorted manner. Thus we will have [1, 2, 3, 4, 6, 8]. In this way, the merge sort program in c will sort the given array.

Pseudocode

• Take two variables left and right
• Declare left variable to 0 and right variable to n-1
• Find mid by medium formula. mid = (left+right)/2
• Call merge sort on (left,mid)
• Call merge sort on (mid+1,rear)
• Continue till left is less than right
• Then call merge function to perform merge sort.

Example of Merge Sort in C

Sorting an Array using Merge Sort

Suppose we are given an array [90, 66, 67, 32, 1011]. We have to sort this array using the merge sort function.

Code:

Output:

Program to Perform Merge Sort

Following is the complete merge sort program in C:

Complexity of Merge Sort in C

Time Complexity

The merge sort is a recursive algorithm. The following will be the recurrence relation for the same:

$T(n) = 2T(n/2) + theta (n)$

upon solving the above relation we can derive that the complexity of the merge sort algorithm is O(nlogn).

The time complexity of Merge Sort is ɵ(nLogn) in all 3 cases (worst, average, and best) as merge sort always divides the array into two halves and takes linear time to merge two halves.

It divides the input array into two halves, calls itself the two halves, and then merges the two sorted halves.

Space Complexity

The merge sort program in C uses O(n) space complexity.

Each call to merge_sort triggers two recursive calls thus if we could deduce that a binary tree of recursive calls is formed although only one of those two recursive calls is performed at a time. The first recursive call ends before the second call starts. Thus, at any given time, only one branch of the tree is being explored. This branch is represented by the "call stack".

The maximum depth of the recursive tree can be log(n), thus the maximum height of the call stack can be log(n).

Now in order to deduce the space taken, we would need to know how much memory would it need in order to explore a single branch.

By looking at the algorithm we can observe that:

At the bottom of the call stack, there is an array of size n. On top of that is an array of sizes n/2. On top of that is an array of sizes n/4 and so on.

Thus the total size of the call stack is at most n + n/2 + n/4 + ... < 2n.

Thus the total size of the call stack is at most 2n which upon omitting the constant gives out the space complexity of O(n).