Python Program to Check Prime Number

Introduction to Prime Number in Python

In this article, we are going to learn about prime numbers and how to check if a number is prime or not. For the testing part, we will go all the way from the brute force method to advanced algorithms like Fermat’s Theorem.

So, let’s start with the definition of Prime Number.

Any positive number greater than 1 is only divisible by two numbers i.e. 1 and the number itself is called a prime number. There is no way to divide a prime number by any other number without getting a remainder. Let's take a look at a few examples to help us understand:

Let's look at the number 11, which can only be divided by 1 and 11. We will receive a remainder if we divide 11 with any other number, such as 5 (the remainder will be 1).

Similarly, finding the factors of 8 yields 1, 2, 4, and 8, indicating that multiple numbers divide 8, hence it is not a prime number.

Now it’s a no-brainer that 2 is the smallest prime number and also the only even number which is also a prime number.

Algorithm to check prime number in Python

So without any further delay, let’s move on to some algorithms which will help us determine whether a given number is prime or not. In this article, we are going to look at the four majorly used algorithms starting from the very basic ones.

Method 1: OLD School Method

The old school method to check if n is prime would be to iterate from 2 to N/2 and check if any number divides N. Why we are iterating till N/2 its explanation is given below. Now if the flag variable taken by us at any point changes from TRUE to FALSE, then the given number is not prime else when the loop will complete we can say it is not dividing by any of its factor except 1 and itself, we can say its prime. Let’s understand how to check whether a number is prime or not with this method.

1. Let’s start with taking input from the user. This will be our number which we want to test whether it is a prime number or not.
2. Declare a flag variable isPrime that is set to TRUE.
3. By the definition of prime number, we need to take a positive number as input even though we will keep a check whether the number is positive or not at the beginning.
4. Now, let’s iterate over the loop from 2 to N/2(number) to check for divisors.
   • Explanation- Since, the lowest factor of any number N can be 2 and it can be written as N = 2 * (N/2), we cannot find any factor beyond N / 2 for it. Thus, any iteration beyond N / 2 is redundant.
5. Set the flag to “TRUE” and break if a divisor is detected.
6. Now check whether the value of the flag is TRUE or FALSE, if it’s TRUE then the number is not prime, else it’s prime.

Pseudocode:

Python Code:

Sample input:

Sample output:

Sample input:

Sample output:

Sample input:

Sample output:

Time complexity: The time complexity of this solution is O(N) because the loop is iterating from 2 to N/2, so the running time is in the order of N. At first glance, you will think that it’s the most optimised solution because it’s running in linear time. But, the truth is far from the right, because this is a valid solution but not the best one available.

In the next method, we will try to optimize this brute force method and improve its time complexity.

Method 2: Optimized School Method

We iterated from 1 to N/2 in the first technique, but now we'll iterate from 1 to sqrt(N) i.e. square root of N. So why are we doing this?

Because the bigger factor of N is composed of smaller factors that have been already calculated.
Since, we are iterating from 2 to X, where $X = sqrt(N)$ and N is the number we want to check whether it is prime or not. So, we can say $X*X = N$. And the product of 2 factors of N is equal to N. So, $X*X = A*B$. Also, X is a real number whereas, N, A, B are natural numbers.
So, now we can formulate three cases.

1. When $A > X$ and $B < X$.
2. When $A < X$ and $B > X$.
3. When Both A and B are equal to X.(This is true only when X is a perfect square).

Since it is one of the factors that A is always greater than or equal to X, so the other factor would always be less than or equal to X. Let's look at example 64, so the factors will be comprised of one smaller factor and 1 bigger factor e.g.

$8*8$, $16*4$, $32*2$.

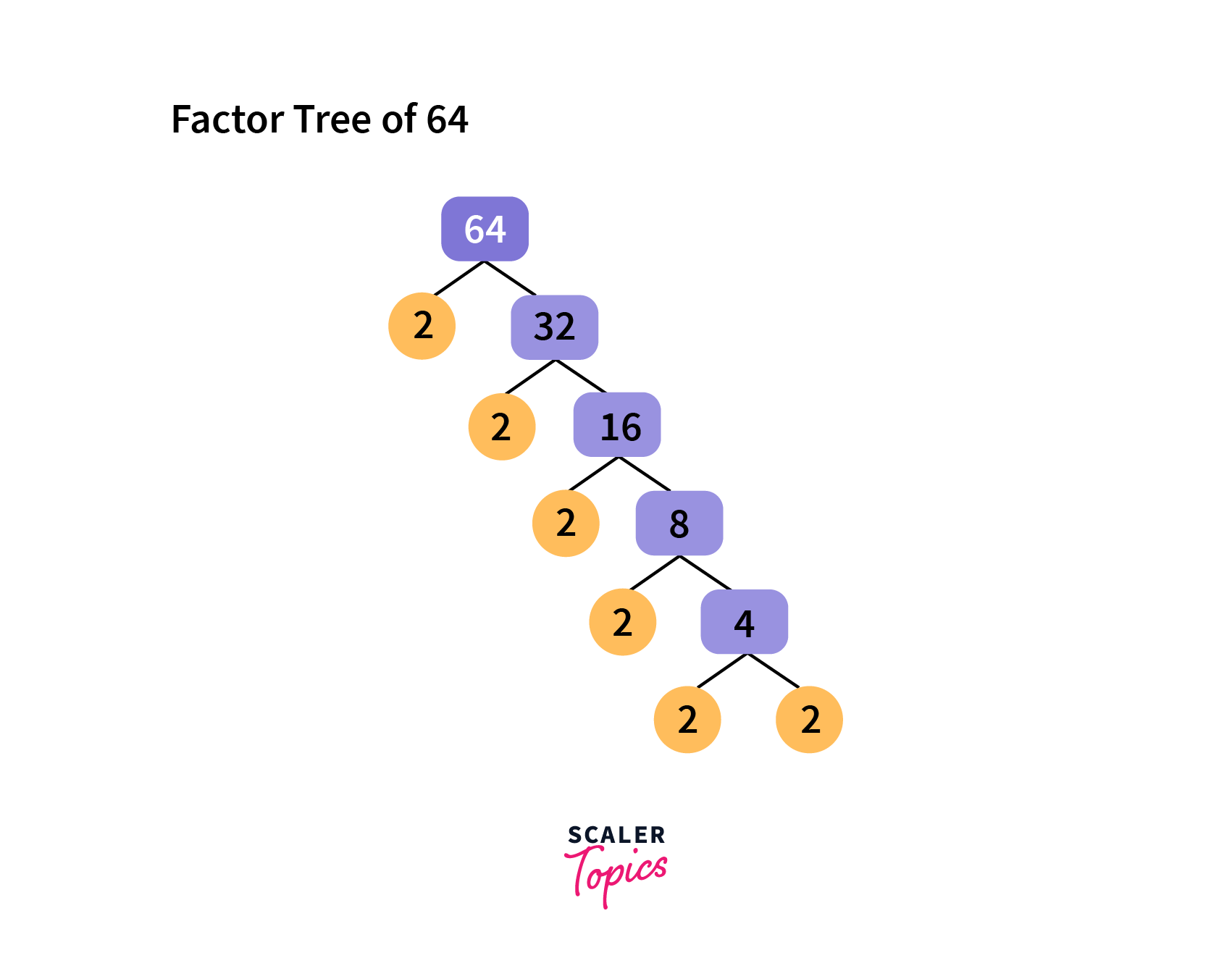
All the steps will be the same compared to the brute method, the only difference is we will iterate the loop from 2 to sqrt(N) i.e. square root of the value of N.

Fun fact: Every prime number can be represented with $6K+1$ and $6K-1$. K can be any whole number. The only exceptions are 2 and 3. Let’s take an example of K=1, then $6K+1 = 7$ and $6K-1 = 5$.

Pseudocode:

Prime Number Program in Python:

Sample input:

Sample output:

Sample input:

Sample output:

Sample input:

Sample output:

Time complexity and Space Complexity: This solution has a time complexity of O(sqrt(N)), which is a substantial improvement over the previous solution.

Also, since the program is running in constant space, the space complexity of the program will be O(1).

Method 3: Fermat primality test Method

Fermat stated that for any coprime integer $a$ and prime number $p$ such that $p$ does not divide $a$, $p$ divides exactly into $a^p$ −$a$.

So, in other words, the following equation holds

But, in normal conditions, this theorem may not be true for composite numbers (numbers with more than two factors).

Let's break down an example for better understanding.

Step 1: Let’s take our prime number(p) = 11, and co-prime number(a) is 2, 3.

Step 2: Using Fermat’s theorem formula of $a^{p-1}\%p = 1$, where $p$ is the prime number and $a$ is the coprime number. Let’s directly use it in the formula. In the case of using $a = 2$, $p=11$, we get $210\ \%\ 11$, which equals $1$. In the case of using $a = 3$, $p = 11$, we get $310\ \%\ 11$, which again results in 1. So, for all the numbers if it’s a prime number it will return 1.

A question may arise if it’s not a prime number. In that case, our given expression i.e. $a^{p-1}\ \%\ p$ will not return 1.

Hence our test will give false as output.

We now know what exactly is Fermat’s Primality Test, but how do we implement it? Few things we need to keep in mind while applying Fermat’s Test are:

1. The higher the value of iteration, the higher is the probability we will get the correct answer. Since the Fermat test is like a trial division method. So, higher iteration will increase the probability as mentioned earlier.
2. For composite numbers, it may be true or it may not, and chances for the correct answer for composite numbers increase if iteration is increased. For prime numbers, it gives the correct answer.

Now, let’s take a look at Pseudocode.

Pseudocode:

Before implementing let’s try to understand the Peudocode, here we are using a function used to calculate the binary exponentiation. It’s a trick for calculating the Nth power of a number in O(log N) complexity instead of O(N). The Binary exponentiation function uses the below formula. Which we will be implementing recursively as writing a recursive code for the formula is the direct translation of formula.

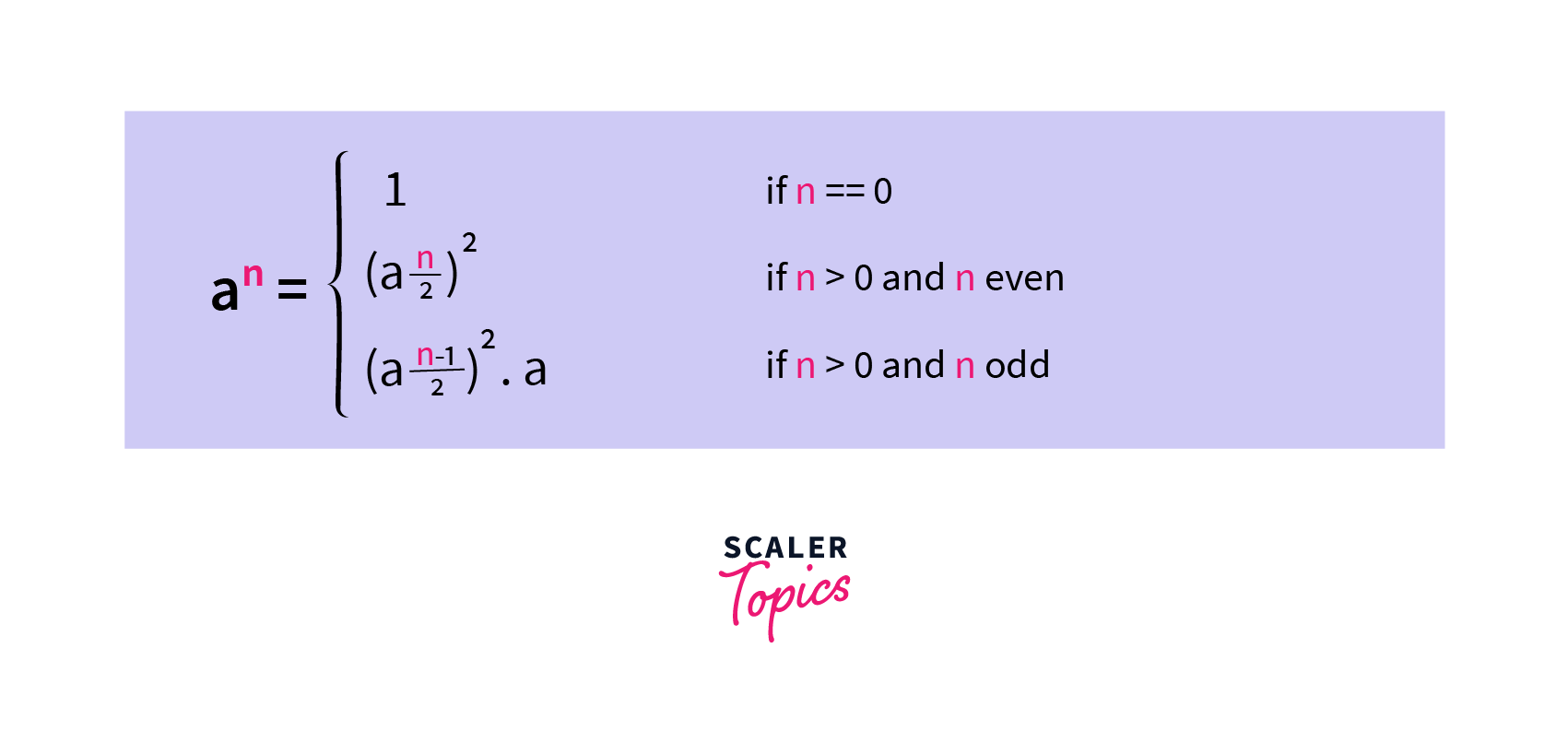
Since we can use any number from 2 to N-2, so it’s better to use any random number as it is a probabilistic test. Then we can simply check if the binary power function holds true or not. Now, let’s implement it in Python.

Prime Number Program in Python:

Sample input:

Sample output:

Sample input:

Sample output:

Sample input:

Sample output:

The complexity of the Algorithm:

Time complexity: O(K*log N). where N is the input number and K is the number of iterations Because log(N) is the time complexity for computing $a^{n}-1$, Here a is the coprime number and n is the prime number, as explained earlier. Since we are using Binary exponentiation, the process is repeated K times. So, the overall time complexity of this algorithm is O(K*log(N)).

Space complexity: O(1), since we are working in constant space.
Although in the case of Carmichael numbers it may fail, these numbers are extremely rare and the Fermat Test is fast, so it’s still in practice.

Method 4: Miller-Rabin Primality Test

We can call it an extended version or improved version of Fermat’s Primality test, why?
Although the Fermat test was really fast, let’s be honest it had its fair share of problems.
So, what were the problems with the Fermat Test? Let’s suppose any composite number N which is not Carmichael, then the probability of N being composite is 1/2 but Fermat’s test will fail in the case of all Carmichael Numbers. However, since in the case of the Rabin-Miller test, there aren’t any hard inputs so the correctness probability of the Carmichael number is independent of that of the probability of composite numbers. Also, there is a mathematical proof, which is a little complex and we are not required to research before writing a program so let’s just look at the equation.

We can factor all the power of 2 by relating $N-1 = D*(2^{S})$ where N is the odd number, so $N-1$ is an even number, S is the prime number and D is another odd random number between 2 to $S-2$. Since Miller Rabin is an improvement over Fermat’s Theorem, thus we can factorize the equation of Fermat’s Theorem.

So, for N to be prime, either

So, now let’s take a look at Pseudocode.

Pseudocode

Fermat’s theorem had limitations in the case of Composite numbers, giving false positives in some cases. Miller tried to overcome it using this theorem, which we will implement as a composite check. As a result, our code can speed up the process. Instead of checking for binary exponentiation we can check for composite and return true or false.

So, let’s implement this PseudoCode

Prime Number Program in Python:

Sample input:

Sample output:

Sample input:

Sample output:

Sample input:

Sample output:

The complexity of the Algorithm:

Time complexity: O(K*log3N). using repeated squaring, where N is the input number and K is the number of iterations.

Space complexity: O(1) since we are working in constant space.

Application of Prime Numbers in Python

In the topic of Cyber Security, prime numbers play an important role because they are utilised in various types of encryption that serve to keep information safe over the internet.
In addition to banks using similar encryptions to protect credit card information, hospitals also use similar encryptions to safeguard medical records, and even WhatsApp uses it for messaging.

Read More:

1. Python if…else Statement
2. For Loop in Python
3. Break, Pass and Continue Statement in Python
4. Numbers in Python