Quick Sort in Java
Learn via video course

Overview
Quick Sort is the fastest and one of the most efficient sorting algorithms that work by partitioning an array into subarrays based on a pivot. A pivot is an element around which the partition is done. The partitioning occurs in such a way that one of the subarrays contains elements smaller than the pivot while the other contains elements greater than the pivot. In this article, we'll be focusing on the implementation of Quick Sort in Java.
Scope of Article
- The Divide and Conquer approach has been briefly explained.
- The article discusses the implementation of Quick Sort in Java and also provides visualization of the working of the algorithm.
- The comparison between Quicksort and Mergesort has also been demonstrated.
- The program for Quick Sort in Java has been explained along with the approach.
Introduction to Quicksort Program in Java
Quick Sort is the fastest sorting algorithm in terms of time complexity in both the average and the best case. It works on the basis of the Divide and Conquer strategy. Partitioning is the specific area that needs attention when Quick Sort is being discussed. The pivot is picked either by selecting a random element or an element at the extreme position (either the leftmost or the rightmost index). Alternatively, a median of the array can also be considered as a pivot. Based on the pivot's position, the other elements are positioned either to its left (being smaller than the pivot) or to the right (being greater than the pivot). Also, the elements equal to the pivot can be placed in any of the two subarrays.
Although the algorithm has been precisely illustrated, we'll be focusing on the implementation of Quick Sort in Java.
QuickSort is an in-place algorithm because, apart from the stack created due to recursion calls, it doesn't require additional storage space to perform sorting operations.
Moreover, QuickSort is an unstable sorting algorithm as it involves the swapping of the elements in accordance with the pivot's position. So, the relative order of the elements isn't maintained.

We will travel through all the above-mentioned terms. The Divide and Conquer approach shall be comprehended properly. The implementation of the same approach will become easier to understand while discussing Quick Sort in Java.
Divide and Conquer approach comprises three steps:
- Split a huge problem into sub-problems (breaking),
- Solve the sub-problems separately (solving), and
- Finally, combine them once again to get the final assortment as per the needed results (combining).

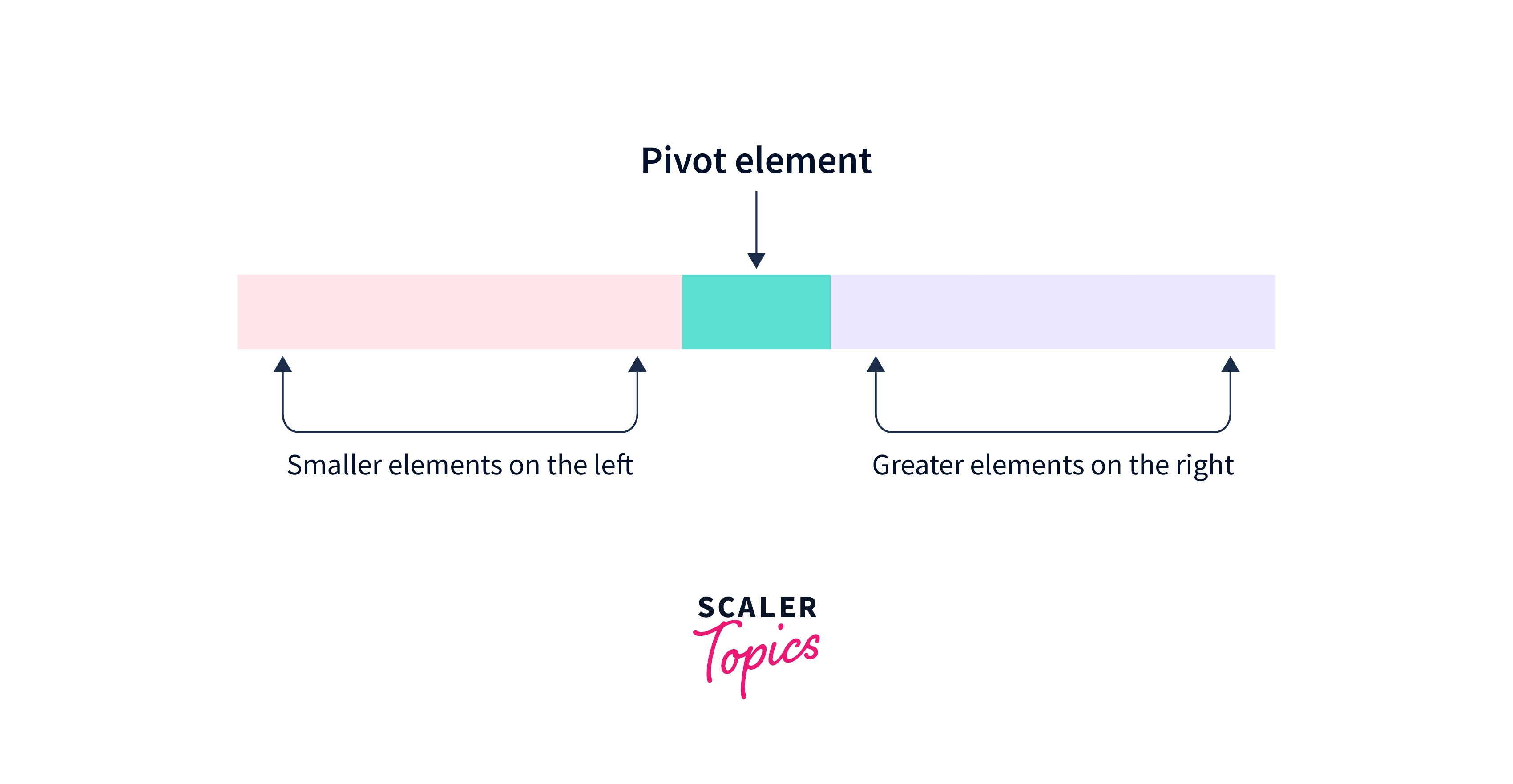
Now, what's a pivot?
In Quick Sort, a pivot is an element that needs to be placed at its appropriate position by swapping and rearranging the other elements around the pivot, meaning that all the elements lying on its left must be lesser than the pivot and the elements on its right must be greater. The basis of every partition in Quick Sort in Java revolves around the pivot.
Moreover, the pivot can be selected from different positions. You can choose to pick either the first element, last element, the median, or any random element from the array.
Note: In our example, we'll consider the middle element as the pivot.
Here's the one that gets the spotlight in a QuickSort algorithm: the partition. The partition should always be in a way where the left side of the pivot strictly contains smaller elements and the right side contains all the greater elements. Elements that are equal to the pivot can be placed on either side.
The Need for QuickSort Algorithm The sole purpose of a sorting algorithm is to rearrange the elements either in increasing or decreasing order to make searching for any element easier. However, there are times when a sorting algorithm might not prove to be helpful when time and space consumption comes into the picture. And in most cases, Quick Sort appears to be the best option among all the sorting algorithms.
How can it be efficient? To begin with, you wish to see the list of items on an e-commerce store to get sorted in the order of their prices. Several internal computations are going on a website at any moment and there's no surety about the total number of your searched item available on the website. And if sorting only takes a lot of time, the experience can never be satisfactory for a user. It has to be quick!
Therefore, we need an algorithm that is not only the fastest but is also less space-consuming. In Quick Sort, the elements arrange themselves according to the pivot's position so that the pivot is placed at its proper position with smaller values on one side and greater values on the other. Since it leads to the creation of two subarrays that are still unsorted, the same recursive algorithm will be applied to both of these subarrays until only a single element is left out for sorting.
Visualization
Steps for Sorting
- An element will be selected as the pivot (middle element in our example).
- The original array would be split into a subarray on the left of the pivot and the other subarray on the right of it.
- The partition will be done on the left subarray and right subarray in the same way.
The Idea for Partition
- Two pointers i and j will be taken where the pointer i is on the leftmost and j is on the rightmost element.
- We'll keep moving pointer I from left to right until we find any element greater than the pivot lying at its left.
- Similarly, pointer j will be moved from right to left until an element smaller than the pivot is found at its right.
- When both the pointer stops due to the above-highlighted conditions, both the elements at positions i and j will be swapped. After swapping, both the pointers will start moving again in their aforementioned direction. It continues until both pointers reach the pivot.
- Finally, we have two subarrays on which the same steps would be performed again until we approach a single element in any of the subarrays.
We have an example of an array, say num, that needs to be sorted with the help of the Quicksort algorithm.
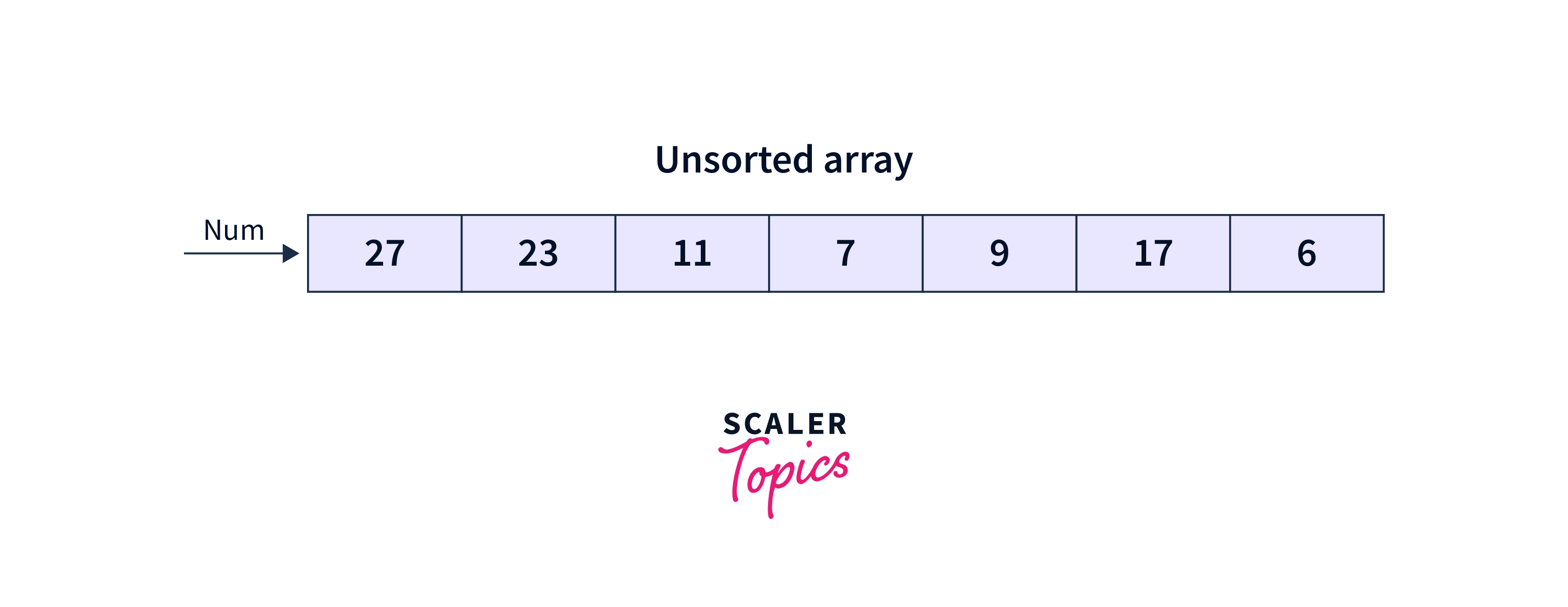
Let us consider a situation where a pivot is a middle element of the array. There is a pointer for the leftmost element as well as the rightmost element. The left pointer moves forward till it finds the elements smaller than the pivot. On the contrary, the right pointer continues moving to the left till it finds greater than the pivot.
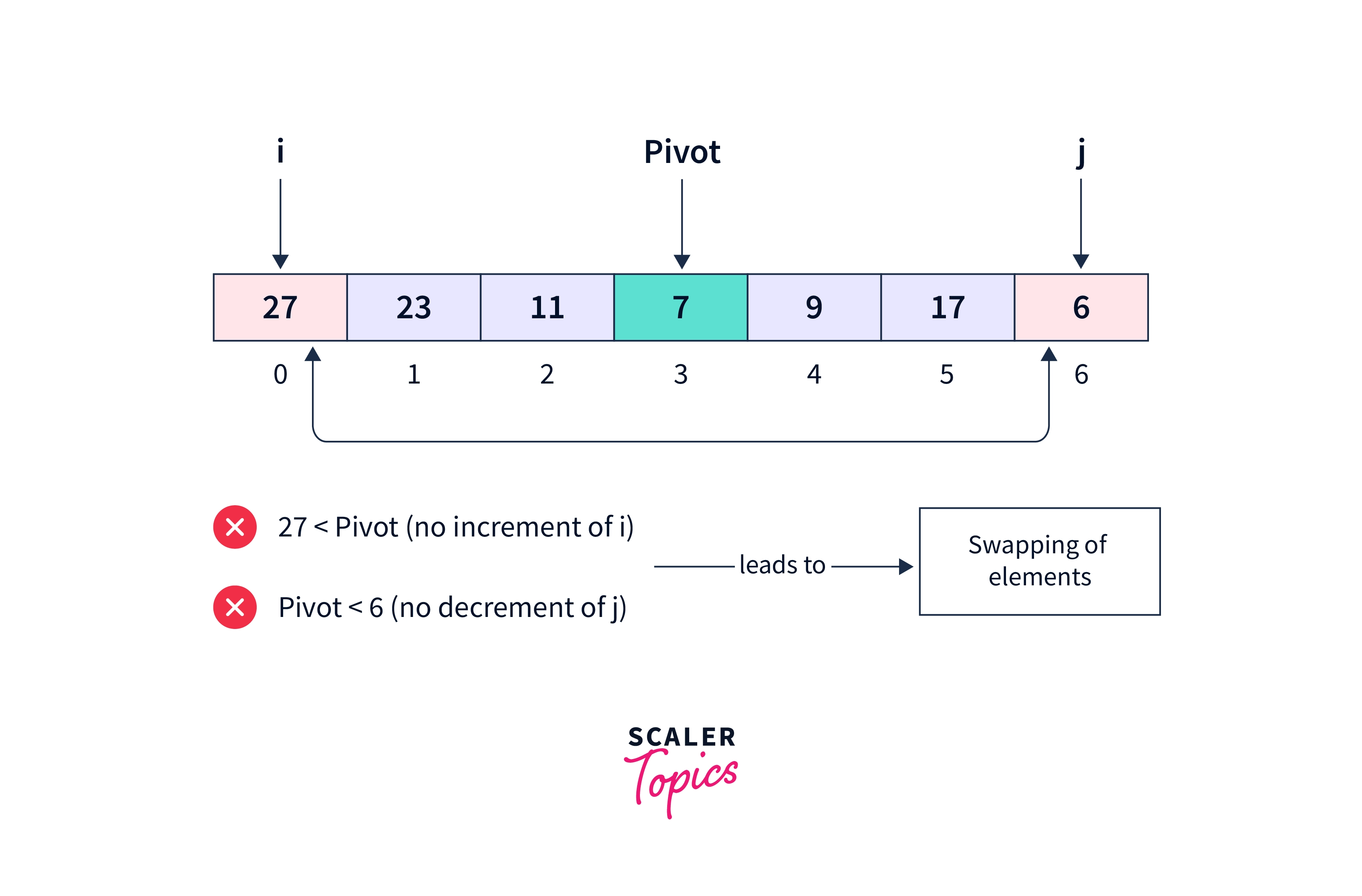
Initially, the pivot will be 7. The element at the 0th index is not smaller than the pivot. Also, the rightmost element at index 6 is not greater than the pivot. So, the pointers stop at this position and wait for the number to get swapped, following which, i increases and j decreases.
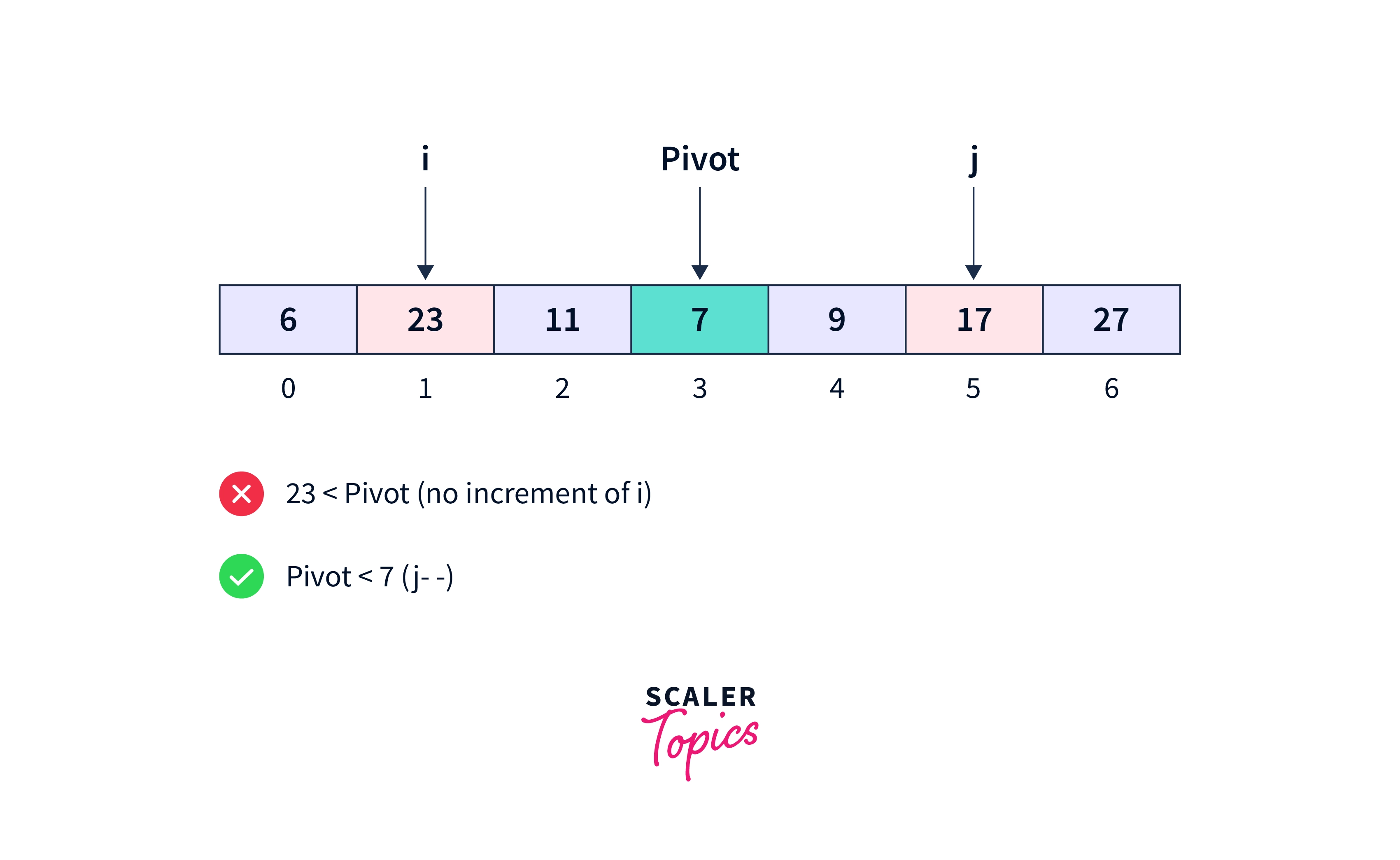
The element at the 1st index is not smaller than the pivot. The rightmost element at index 5 is greater than the pivot. So, the pointer i stops at this position while j gets decremented.
Again, the element at the 1st index is not smaller than the pivot, so the left pointer stays at index 1. The rightmost element at index 4 is greater than the pivot. So, j gets decremented.
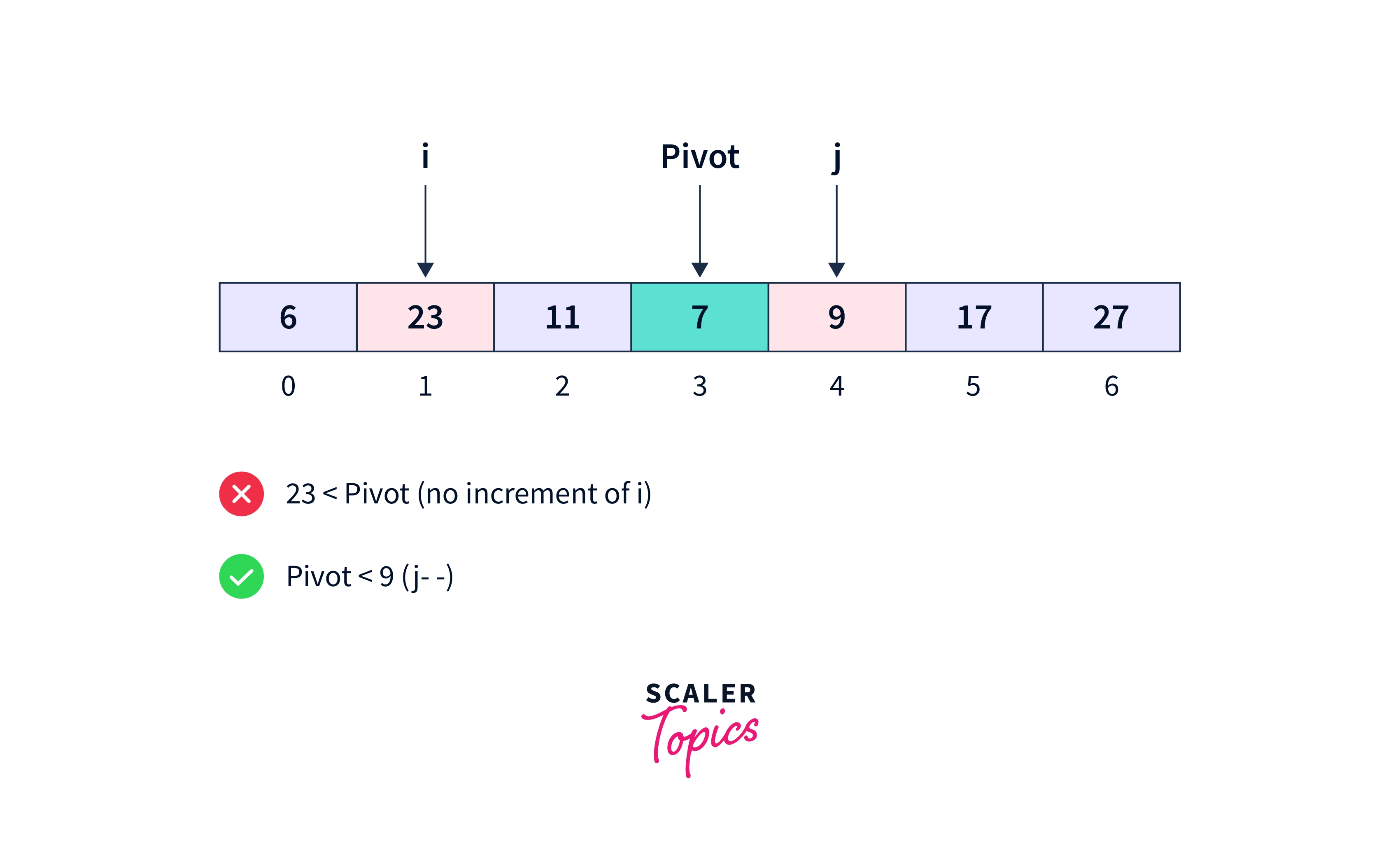
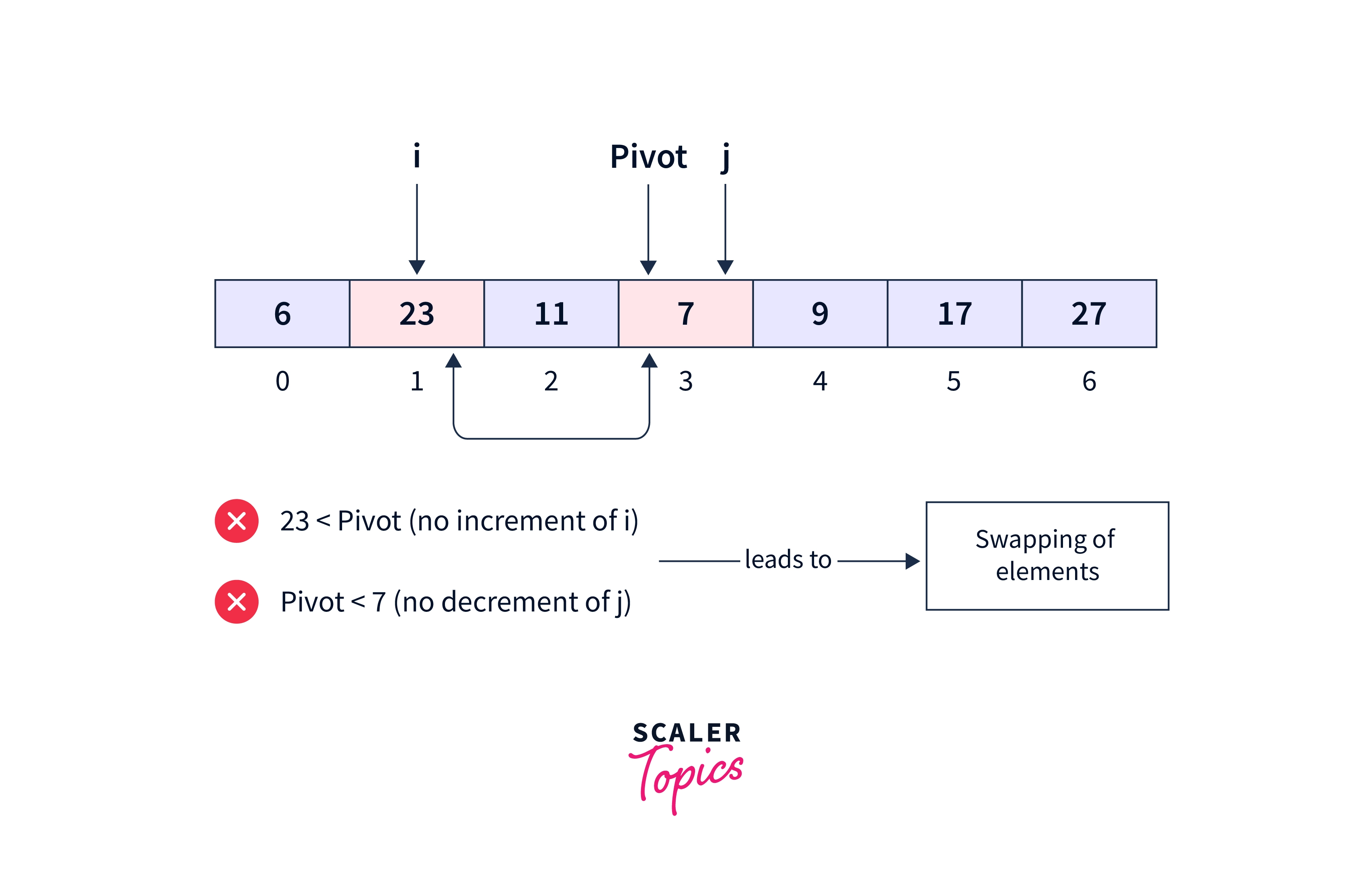
Now, the element at 3rd index is the pivot itself, which cannot be less than itself (upon checking if num[3]<pivot), so this is where pointer j stops and the elements 23 and 7 are swapped. Then, i increases while j decreases.
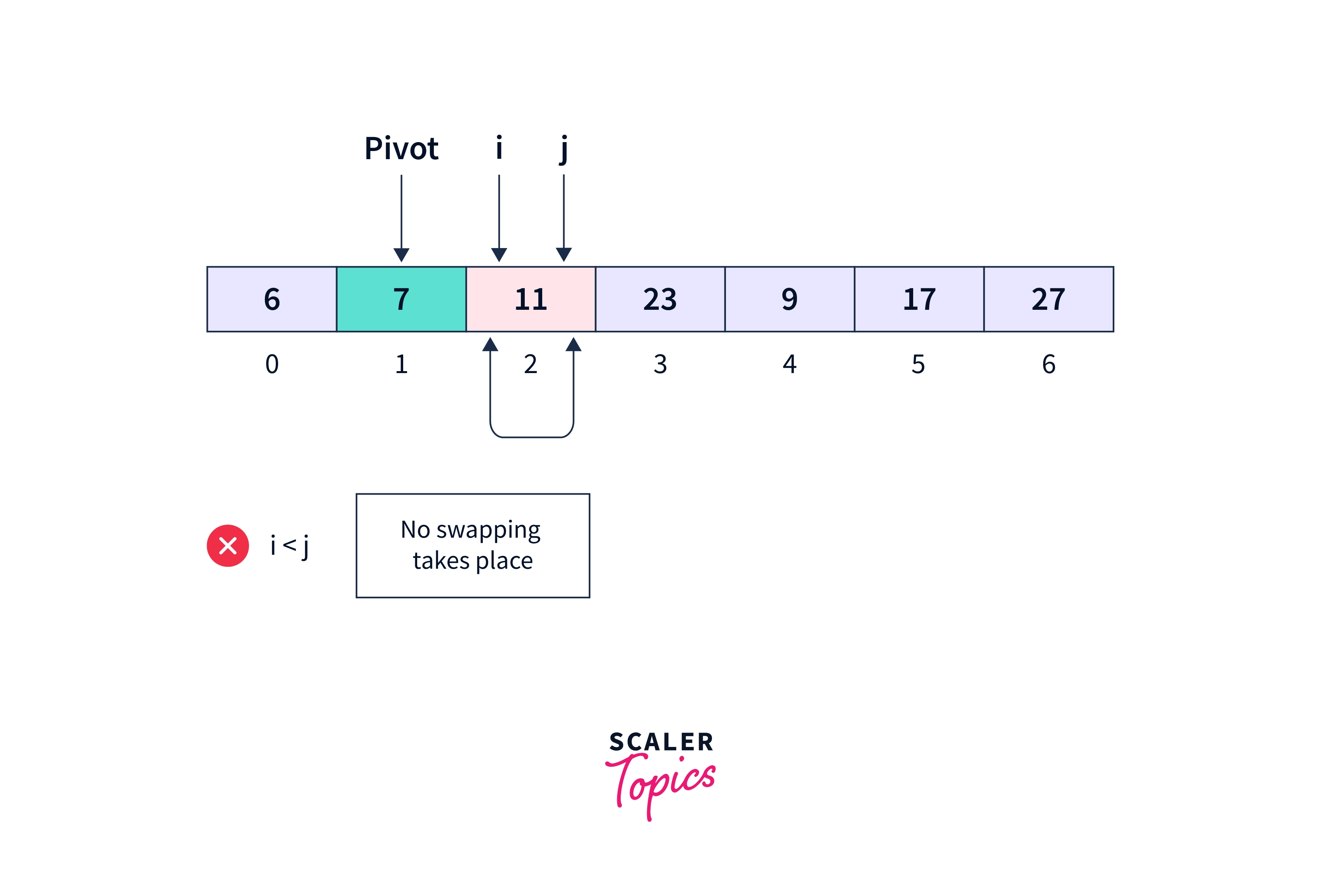
When pointer i and j are at the same position, the loop terminates and finally, pivot 7 is now at its appropriate position. Now, the same recursive quick sort method will be called on the left as well as the right subarrays.
Element 6, being the only element in the left subarray, is already sorted. So, we need to perform Quicksort on the right subarray in the same manner as we did above.
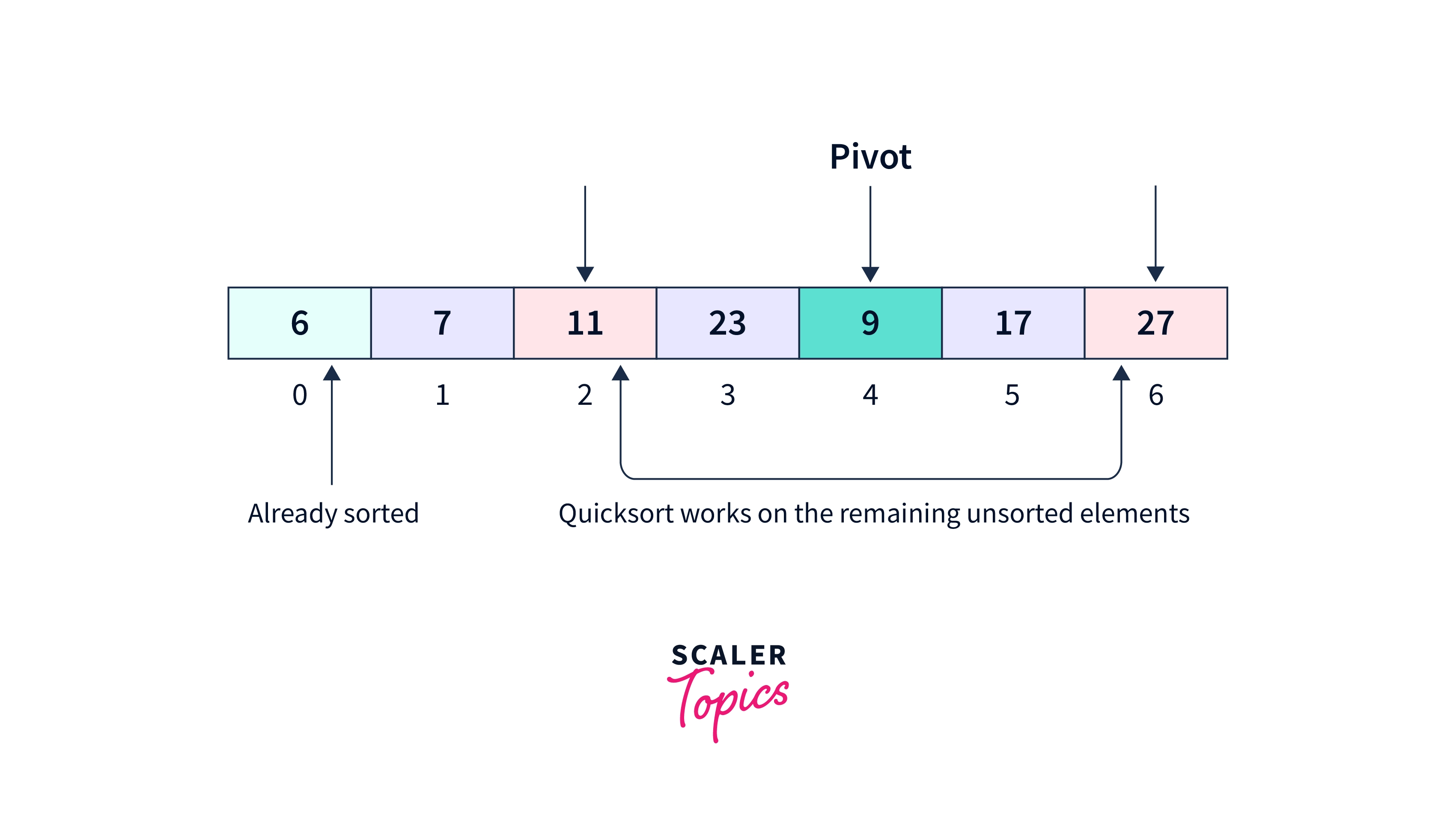
Finally, the sorted array would be obtained.

Pseudo Code for Recursive QuickSort Function
Pseudo Code for Quick Sort in Java
Pseudo Code for Partition of Subarrays
To understand how the pseudo code for partitioning works, revisit the steps given below.
We will now be looking at the program to implement Quick Sort in Java. Moreover, the same pseudo-code for partition and QuickSort function can be used to implement QuickSort in other programming languages.
Example: Java Program to Implement Quick Sort Algorithm
Output:
Time Complexity
Best case Let us see the ideal condition where Quicksort works the best. The best scenario would be to have two evenly split subarrays on either side of the pivot. In other words, the pivot will always be in the middle of the array. The partition also depends on the number of inputs (N).
- If N is odd, then apart from the pivot, both the subarrays will be equal in length, having (N-1)/2 elements each.
- If N is even, then the difference between the size of the subarrays would be 1 as one of the subarrays will have one more element than the other. So, one of the subarrays will have (N/2)-1 elements while another will have N/2 elements.
A quick look at the length of the subarrays makes it clear that any of these two subarrays cannot have more than n/2 elements. So, if we construct a tree, here's what their implementation would be like:
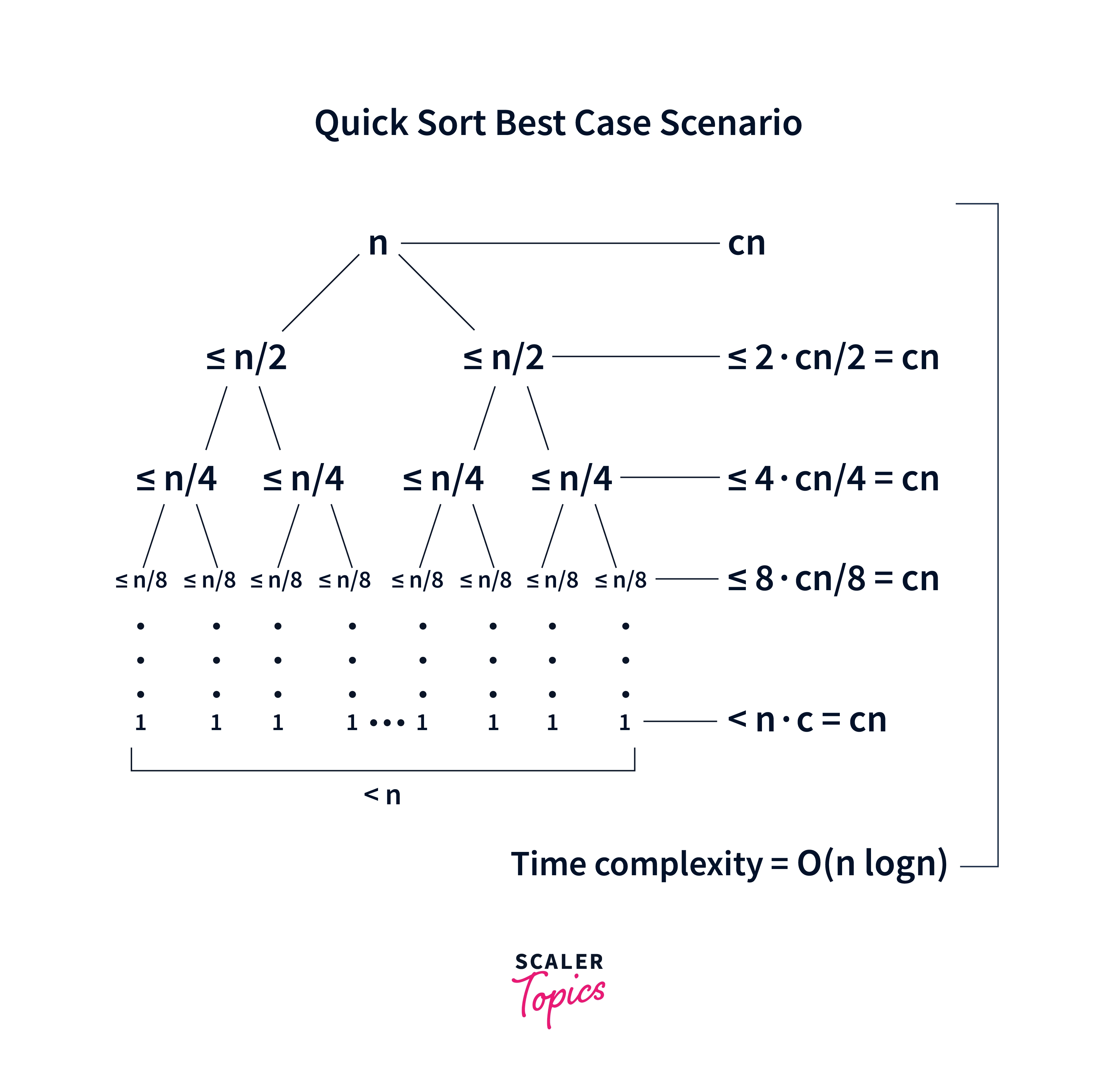
The tree is actually a binary tree as each of its nodes has two elements. The height of a binary tree is . Moreover, the partitioning has to take place for the entire array, so basically, the partition function will traverse through every element in the array, which results in time complexity.
Therefore, the best case for Quicksort would be .
Worst case
It will be a blunder to have an unbalanced partition where the pivot lies at either the leftmost or the rightmost position. In each recursive call, only one item would be sorted and the remaining elements will be left out for sorting at the next level.
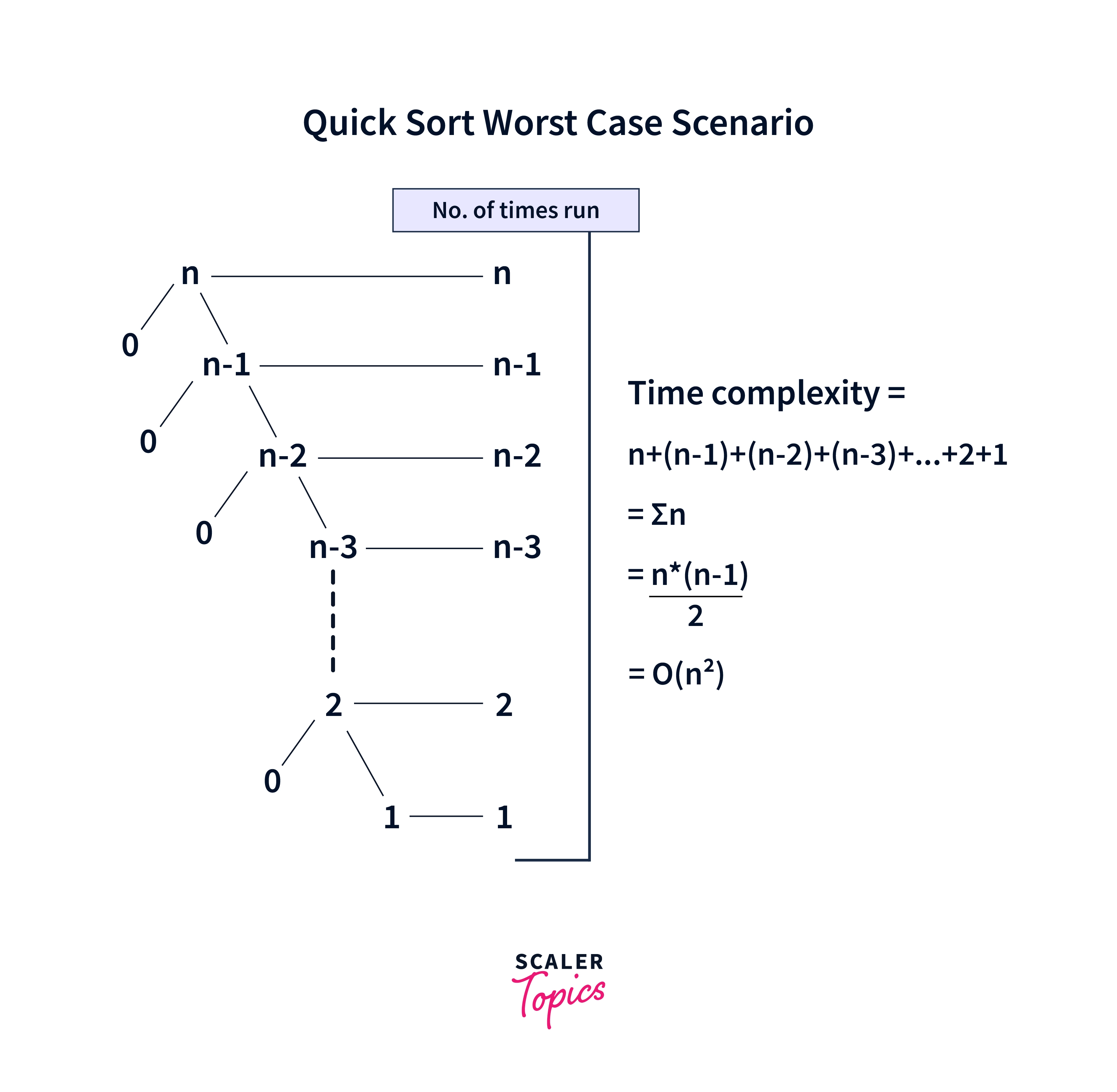
The initial call will consume T(N) time, the second call will consume T(N-1) time, and so on. If we measure the total time consumed in sorting, it will be the sum of all the recursive calls.
QuickSort vs MergeSort
Although there seems to be a head-to-head competition between the two, both these algorithms are useful in varied areas.
Time Complexity Analysis
QuickSort does have an average time complexity of and so does the MergeSort. However, from a theoretical perspective, the worst case time complexity of QuickSort is but MergeSort still works well in even in the worst-case scenario.
The efficiency of QuickSort depends more on the selection of the pivot and it isn't always expected that the best pivot would be chosen. However, the pivot selection is ensured to happen in a way that doesn't increase the time complexity to a greater extent. So, in the average case, the time complexity of QuickSort remains .
Space Complexity Analysis
When it comes to space complexity, QuickSort appears to be better than MergeSort. QuickSort, being an in-place algorithm, doesn't require any extra space and has a space complexity of . The in-place partitioning requires space whereas the number of comparisons will lead to space in the average case but in the worst case (N recursive calls). MergeSort, on the other hand, requires a new array to store the elements after merging and it has a space complexity of .
Usage
QuickSort finds its use in the case of Arrays because it uses indexing to swap and sort the elements. However, since Linked List doesn't use consecutive address blocks to create nodes and there would be no indexing, MergeSort is used to sort the nodes in a LinkedList without the need for extra space.
Size of Datasets
QuickSort is efficient and faster only in the case of small datasets because, in larger ones, there will be more comparisons which take the QuickSort algorithm near to its worst time complexity. MergeSort, on the other hand, will be better for datasets of any size, be it small or large.
Stability
QuickSort is an unstable algorithm because it doesn't maintain the original order of the duplicate elements due to swapping. However, certain modifications in the code can make it stable. However, in MergeSort, the duplicate elements will have the same position as they had in the input array.
Locality of Reference
In the case of QuickSort, as the elements are placed at consecutive memory locations, so accessing the elements is sequential. So, QuickSort is a cache-friendly algorithm which gives it an advantage over MergeSort
| Comparison | QuickSort | MergeSort |
|---|---|---|
| Time Complexity (Average case) | ||
| Space Complexity (Average case) | ||
| Usage | Arrays | LinkedList |
| Ideal for | Small datasets | Small as well as large datasets |
| Stability | Unstable | Stable |
| Cache-friendly | Yes | No |
The choice between QuickSort and MergeSort shall be made as per the size of the dataset and the data structure being implemented. QuickSort is preferred for Arrays while MergeSort is preferable for Linked Lists.
FAQs
1. How does a Quicksort Work?
Quicksort uses the divide and conquer approach by selecting an element from the array as a pivot and then partitioning the other elements by putting the smaller elements on one side and the greater elements on the other side.
2. What is the Time Complexity of Quicksort?
Time complexity analysis:
Best case:
Average case:
Worst case:
3. Where is Quicksort Used?
- Quicksort, being the fastest algorithm, is used to search for information on several websites.
- It is used for computations related to sorting by price values of items in the case of commercial websites.
- It is more preferred to sort arrays.
4. What is the Advantage of Quicksort?
- Quicksort is an in-place algorithm because it needs only a small stack as its auxiliary data structure for sorting. Plus, it doesn't require any extra space for storing the sorted elements.
- The inner loop used in Quicksort is shorter as it comprises only a few iterations while arranging the elements.
5. Why is Quicksort Better than the Mergesort?
A Quicksort only has an issue of worst-case time complexity. But it also has a time complexity of in the average case, which is the same as that of the Mergesort. On top of that, Quicksort has only space complexity while the Mergesort has space complexity.
Conclusion
- Quick Sort is an efficient and also the fastest algorithm that partitions the array into subarrays with the help of a pivot.
- QuickSort is an in-place, cache-friendly but unstable algorithm.
- A pivot is an element in the array around which the partitioning occurs. A pivot can be:
- a random element,
- the leftmost or the rightmost element,
- a median of the array
- One subarray comprises values lesser than the pivot and the other subarray includes values greater than the pivot.
- Time Complexity:
- Best case:
- Average case:
- Worst case:
- Space Complexity:
- Best case:
- Average case:
- Worst case:
