sqrt() in Python
Learn via video course

Overview
Have you been lately working on some mathematical problems around square roots? Well, the below module has the answer to your problems. You can simply import the math module and use the sqrt() in python to calculate the square root of any number without using any nested loops in python.
An sqrt() in python is an inbuilt function that helps to find the square root of any number that is greater than or equal to zero.
Let us start learning the sqrt() in python along with various code examples.
Syntax of sqrt() function in Python
The syntax sqrt() in python is as below:
where you first import the math module and then you can start using the sqrt() in python. The parameter 'n' in the syntax is any number more than or equal to zero.
Quick Tip − The sqrt() function in python cannot be used directly while writing the code. Hence, to call the sqrt() function in python, we first need to import the math module. Then, to execute this function we need to start by calling the sqrt function in python using the math static object.
Parameters of sqrt() in Python
The parameters of sqrt() in python are as below:
n : To find the square root of any number we need to specify the number in the parameter section.
We need to ensure that the number we are passing as a parameter is always more than or equal to zero. If it is less than 0, then we may encounter will a ValueError. While if the value is not a number, it will output a TypeError.
Return Values of sqrt() in Python
The return values of sqrt() in python are as follows:
The output returned from the square root of the number is a floating-point value for that number that is being passed in the parameter. For example, the square root of 25 would be 5.0 and not 5 as an output.
Exceptions of sqrt() in Python
The only exception of sqrt() in python is to always pass the parameter as a number more than or equal to zero.
If we pass a negative number as a parameter it returns a 'ValueError'.
While if the value is not a number, it will output a TypeError.
Example of sqrt() in Python
Let us look at a small and crisp code example where we shall be implementing the sqrt() function in python to implement all that we studied above. This example will walk you through how we can implement the sqrt in python and find the square root of any number ( positive and zero) with the help of python.
Code:
Output:
Explanation: We start by importing the math module, where the sqrt() function in python is already present as an inbuilt function. Then we use the sqrt() function in python to find out the square root of various numbers (in this case 4, 9, 16, 0) that we defined in various variables. Finally, we print the variable and we get the desired output.
What is sqrt() in Python?
Are you finding it difficult to calculate the square root of a number by using a nested loop in python? Well, have you heard of the math.sqrt() function from the math module.
The sqrt() in python can be defined as an inbuilt function in the python language which is an easy way of getting the square root of any number that is more than or equal to zero. No more looping the for loops to calculate the square root of a number, you can simply use the math.sqrt() in python to calculate the square root of a number. The math module is a standard python library that has various inbuilt functions of which, we shall be exploring the sqrt() in python. Now when you want to find the roots of a quadratic equation or be it calculating the length of one side of a right triangle, you can simply first import the math module and start using the inbuilt sqrt() in python to calculate and solve your problems. The sqrt() in python outputs the number as a float type and not an integer type.
Quick Tip: The number that is passed in the parameter has to be more than or equal to zero for the math. sqrt() in python to work and generate results.
As shown below you start by importing the math module and start directly using the sqrt() function in python to calculate square roots:
In the output, you will always find that the number returned is a floating-point number, not an integer.
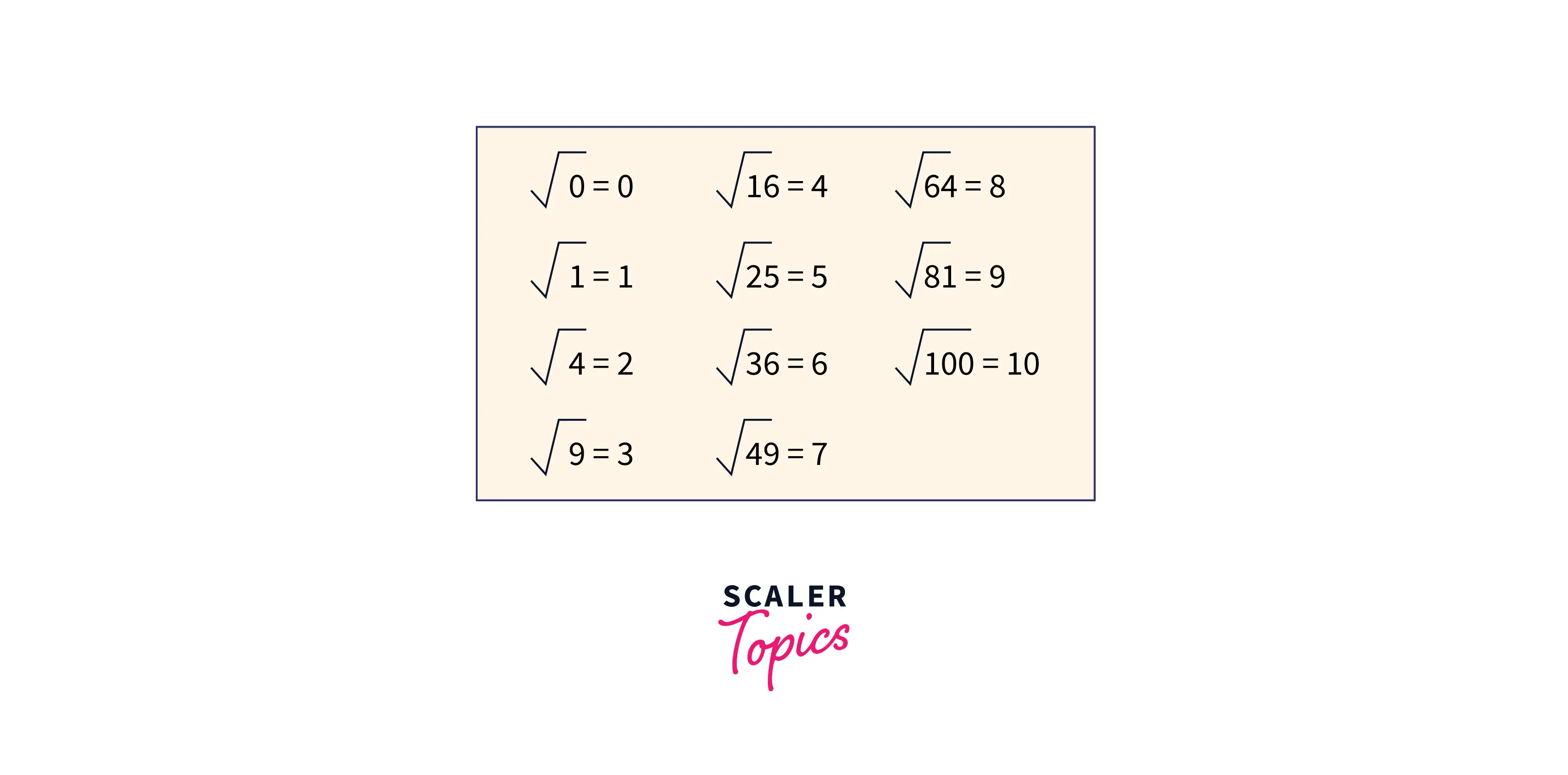
The below diagram shows a simple illustration of the sqrt() in python:

More Examples
Now that we have understood the concepts around the sqrt in python, let us start practising it with a few code examples as listed below:
Square Root of a positive number
Code:
Output:
Explanation: As seen above, we are printing the square root of the Positive Number (integer and float values). We have used the square root syntax we learned before to find the square root of the positive number. We imported the math module to use the square root syntax.
The square root of zero
Code:
Output:
Explanation: As seen above, we are printing the square root of Zero by using the square root syntax we learned before to find the square root of zero. We imported the math module to use the square root syntax.
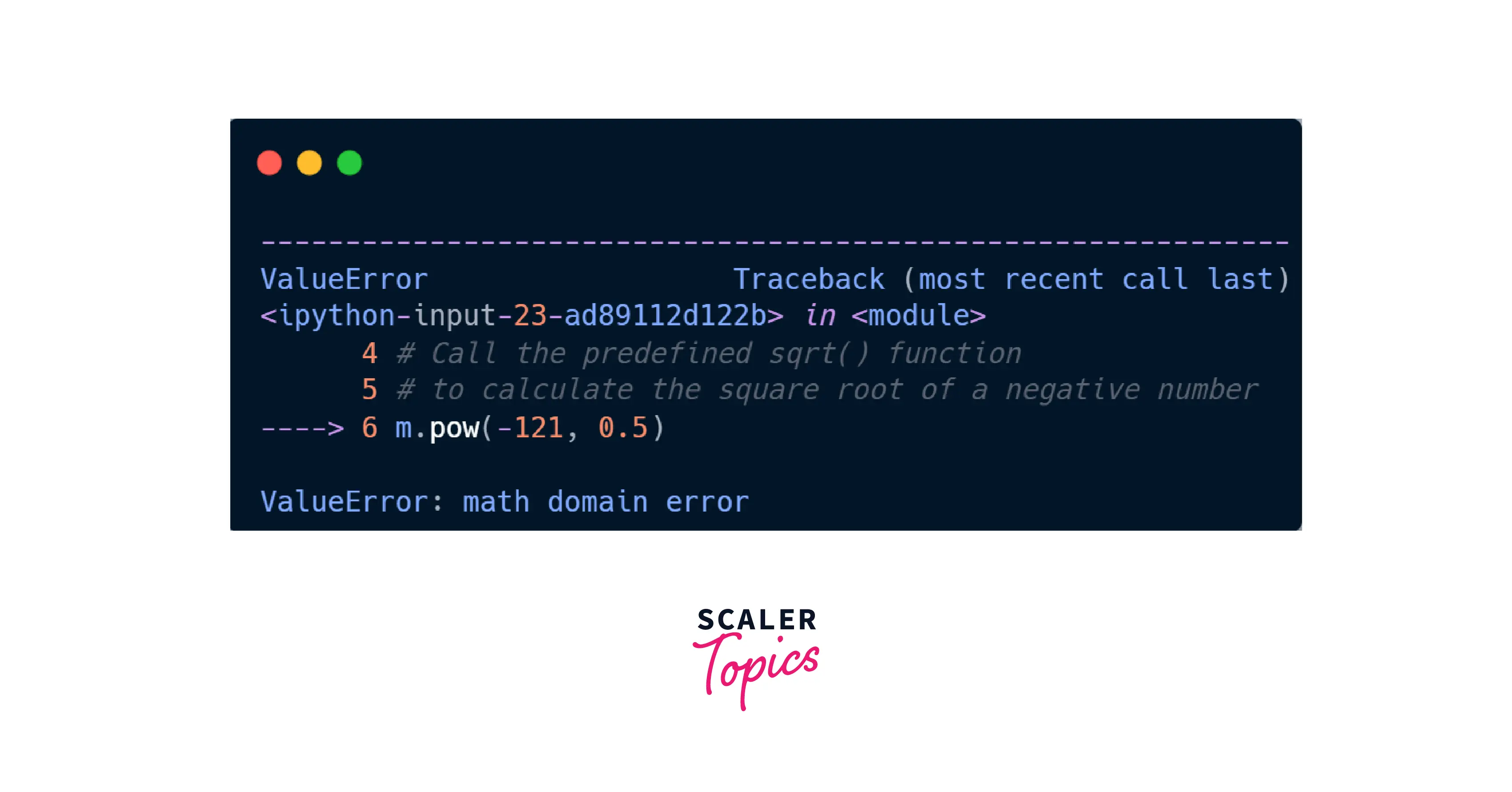
Square root of negative numbers
Code:
Output:
Explanation: As studied above for any number less than 0 or a negative number, the square root for that number comes out to be an ERROR as we got for the above code where we were trying to sort import the math module to use the square root of the number -9. And once the code was executed we get a ValueError: math domain error .
Given a number, check if it is prime or not demonstrate the error in the sqrt() method
The below code explains how we can make use of the (sqrt9) in python to calculate if a given number that is entered by the user is prime or not.
With the below code, we first start by importing the math module, moving to define a function named prime_check which will check if a given number when divided gives any remainder or not. If the number does not give a remainder or the remainder comes out to be zero, then we can say that it is not a prime number else it is a prime number( if we see any remainder occurring)
Code:
Output:
Explanation: here we are defining a function that will be used to check if a number is prime or not. Then we are
Real-world application of the Python square root function
Since we have explored various scenarios to find a number's square root, let us use the learning so far and see a real-world application of the python square root function.
We shall be exploring the popular game of tennis to expand our vision to understand the concept of sqrt() in python.
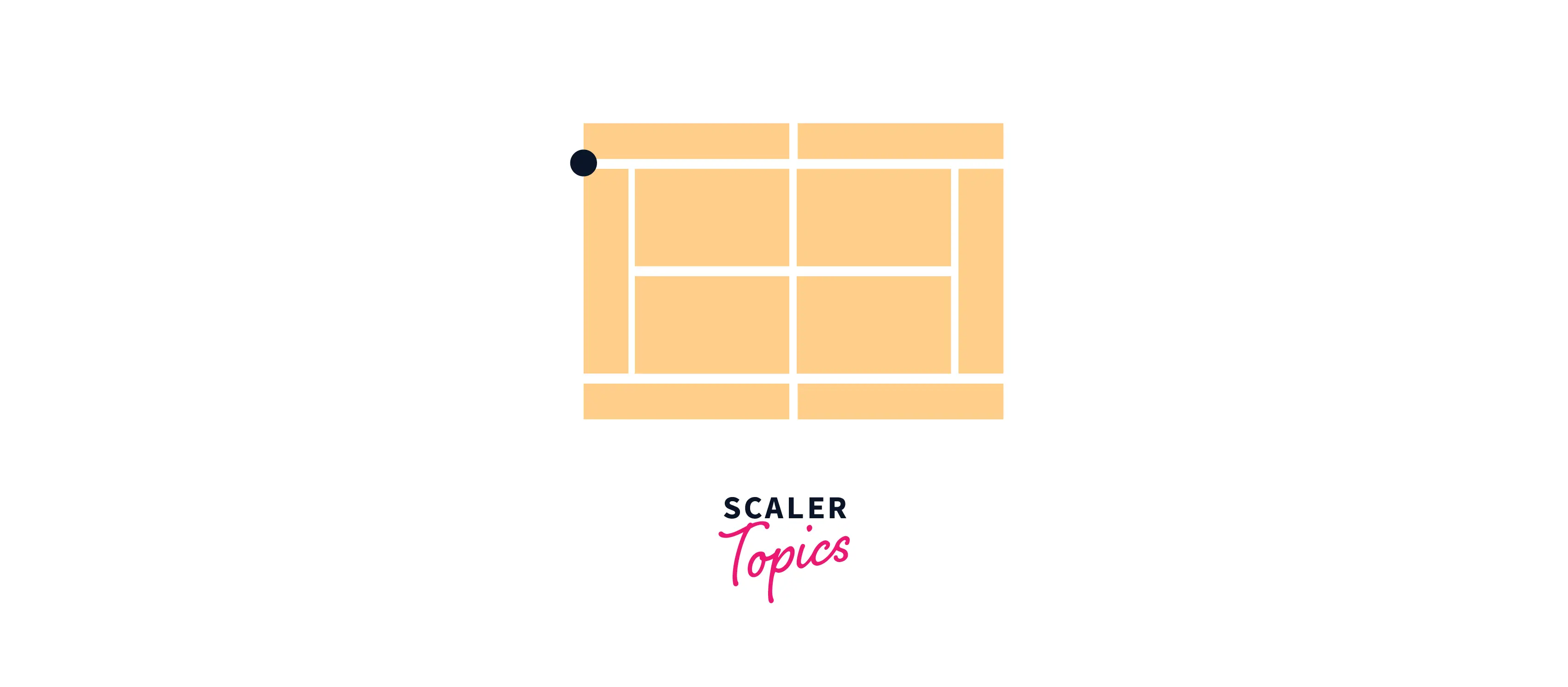
Suppose you are playing tennis and from the back corner you just hit a forehand. Exactly where the baseline of the tennis court meets the sideline as shown below.
Assuming the opponent counters this shot of yours with a drop shot. A drop shot is one in which the ball short is placed with a little forward momentum. This drop shot hits the opposite corner and eventually meets the nets on the other sideline as observed below:
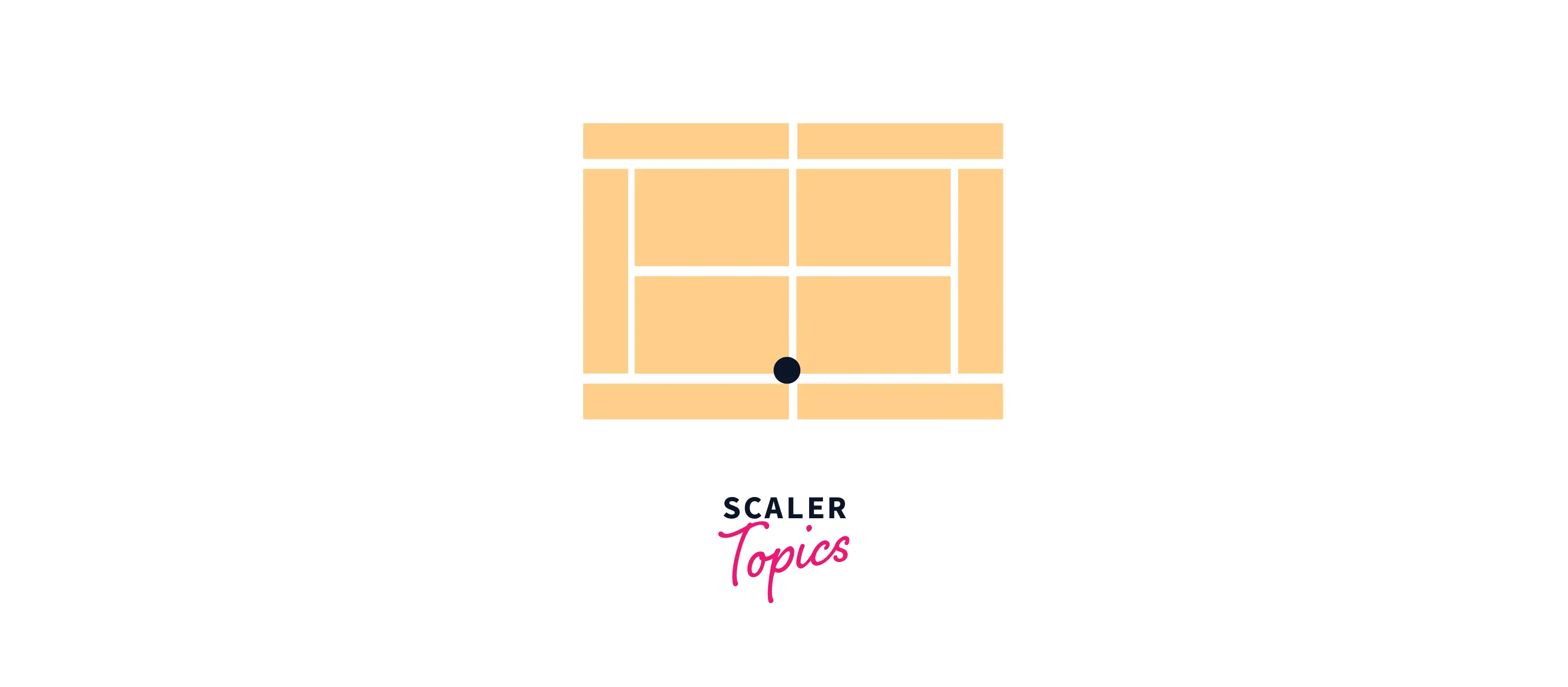
Now the question goes like this, How far will you need to run to reach that ball?
Interesting right? We may refer to the regulation of tennis court dimensions where we may know that the baseline is 27 feet long, and the sideline measures 39 feet long. Now, we are solving the problem of finding the hypotenuse of a right triangle as shown in the below diagram
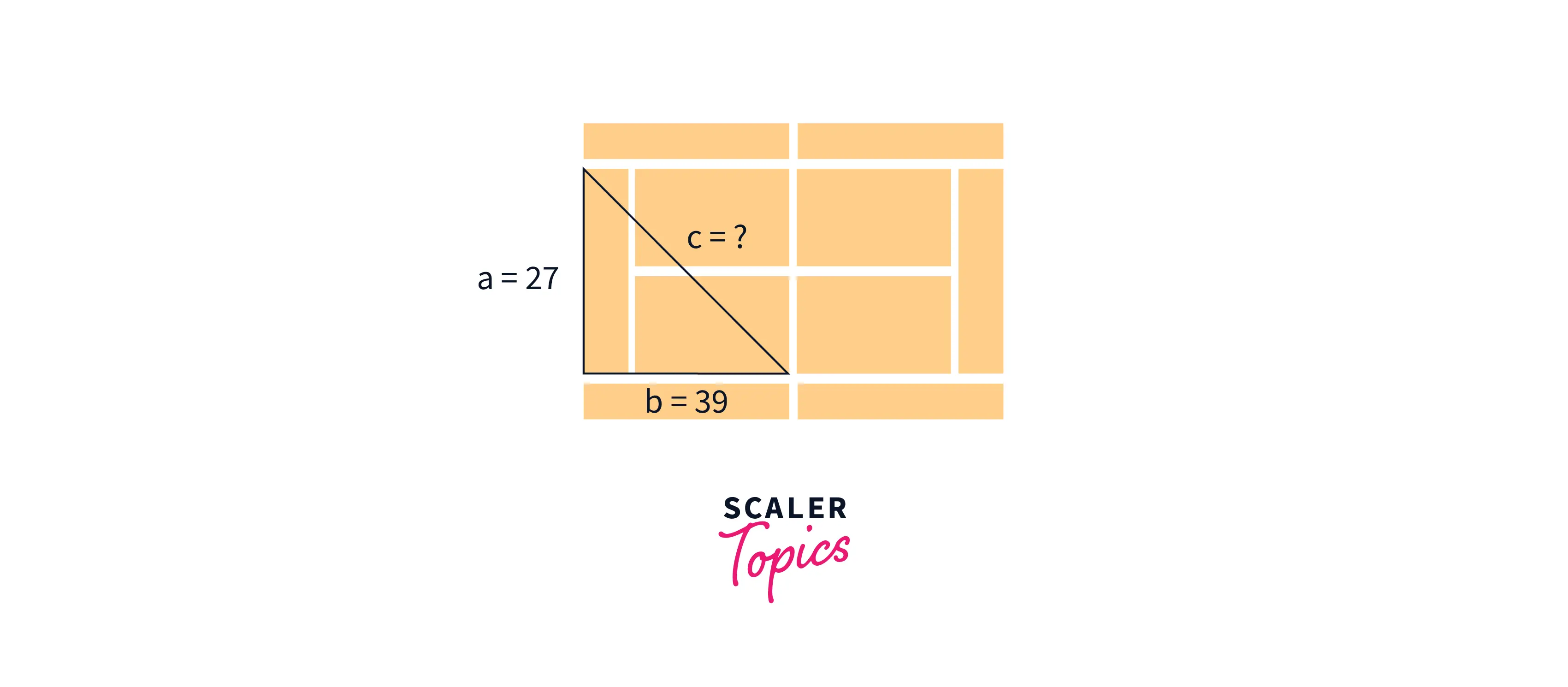
As studied in mathematics, the Pythagorean theorem is mathematically stated as a² + b² = c² where a and b are the perpendicular and base of the right triangle and c marks the hypotenuse.
Now to calculate the distance that you need to run, we shall be equating the equation and using the sqrt() in python to solve for the c as follows:
Code:
Output:
Explanation: As seen via the output, you need to stretch and run 47.4 feet to reach the ball and win your point.
Conclusion
- An sqrt() in python is an inbuilt function that helps to find the square root of any number that is greater than or equal to zero.
- If you use the sqrt in python to find the square root for any negative number you shall encounter a Value Error.
- While if the value is not a number, it will output a TypeError.
- The output returned from the square root of the number is a floating-point value for that number that is being passed in the parameter eg 5.0 not 5.
- Various scenarios covering the concepts around sqrt() in python were covered as learned in the above code examples.
