Merge Sort Algorithm

Introduction to Merge Sort

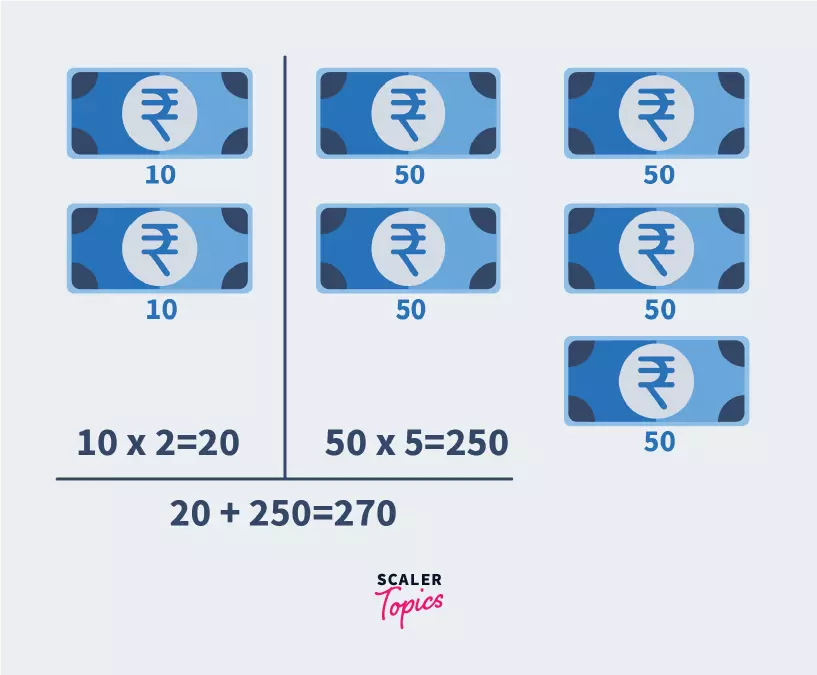
Imagine a situation where you have a lot of money of different denominations and you need to calculate the total amount of money you have.

What do you do?

Well, Wouldn’t it be easier if you first divide the money on the basis of the denominations i.e. all the 10 rupee notes in one pile, all the 50 rupee notes in one pile, and so on, and then find out the amount of money in each pile, and then sum the total amount of each pile to get the amount of money you have?

As in, if you have two 10 rupee notes and five 50 rupee notes, you would first find the sum of the 10 rupee notes i.e. $2*10=20$ rupees and $5*50=250$ rupees, and finally sum this, $20+250=270$ rupees.

We need to count the total money we have:

We organize it like so to make things easier.

Merge Sort is one of the most respected sorting algorithms, with a worst-case time complexity of O(nlogn).

Merge sort works by dividing the array repeatedly to make several single-element arrays.

The concept of merge sort involves breaking down an array of n elements into n individual elements. Why?

As each element can be considered as a sorted array consisting of one element. Then we start to combine these individual single array elements into one final sorted array.

Merge Sort Algorithm

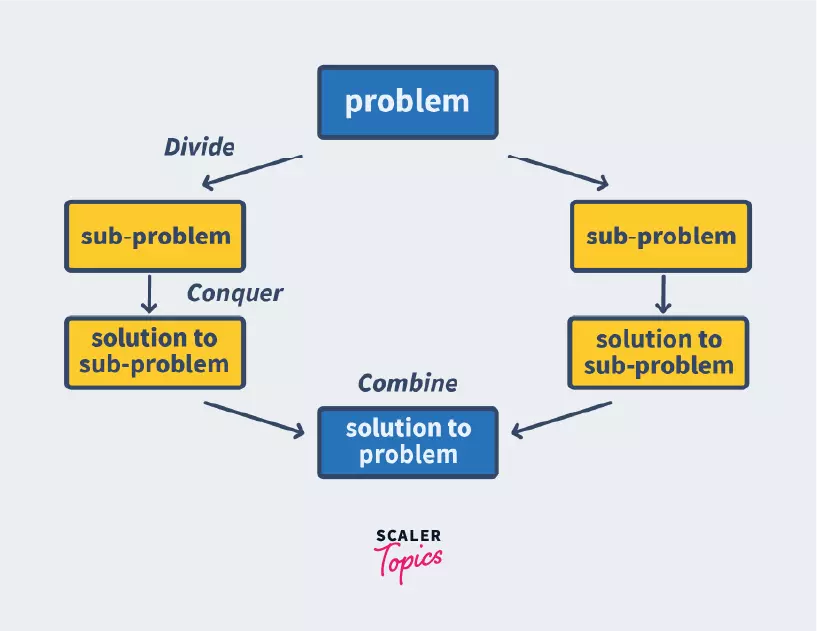
As mentioned earlier, Merge Sort uses the Divide and Conquer Algorithm where a problem is solved by dividing it into numerous sub-problems, conquering each of the sub-problems individually, and then combining it to form the end result, just as shown in the picture below.

How Does the Merge Sort Algorithm Work?

Divide and Conquer Strategy

Now that we have a fair understanding of what divide and conquer is, let us try and understand how that is done to sort an array of integers.

Let us consider an array, arr that consists of n unsorted integers. Our end goal is to sort the array.

Let us consider an array={38,27,43,3,9,82,10}.

1.Divide In this step, we find the midpoint of the given array by using the formula mid=start+(end-start)/2

2. Conquer In this step, we divide the array into subarrays using the midpoint calculated. We recursively keep dividing the array and keep calculating the midpoint for doing the same. It is important to note that a single array element is always sorted.

So, our aim is to continuously divide until all elements in the array are single array elements. Once that is done, the array elements are combined back to form a sorted array.

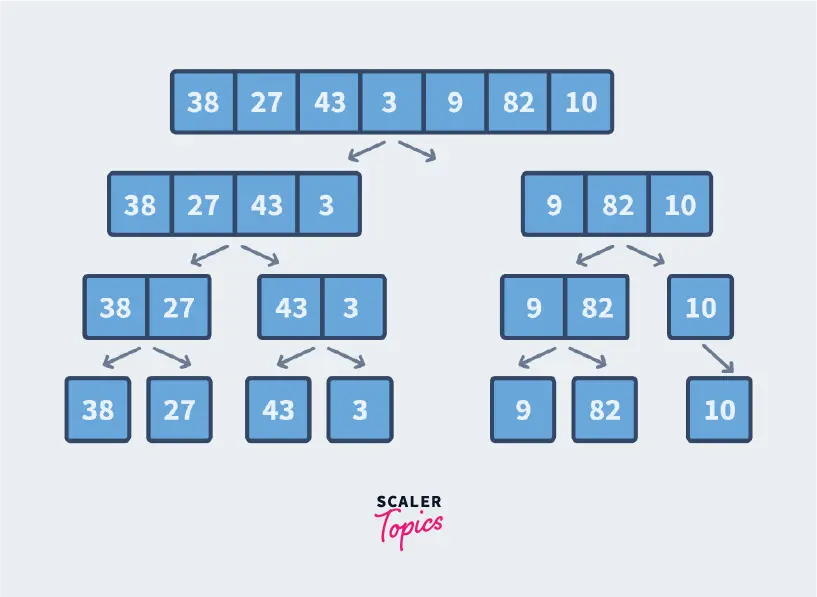
As mentioned above, our goal is to keep dividing till all elements in the array are single array elements hence, this is the base case i.e. when there are n subarrays of the original array that consisted of n integers. It is now the turn is to sort them and combine them.

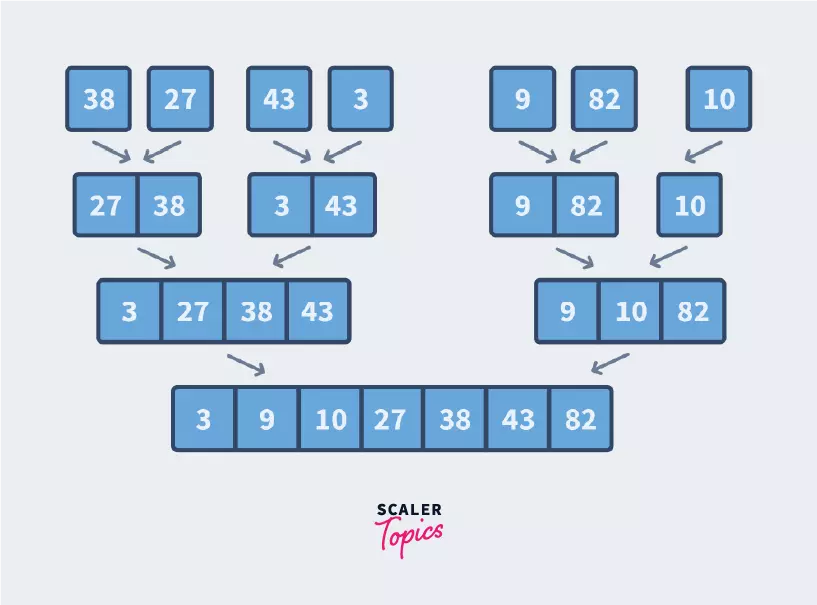
3. Combine

Now that all our subarrays are formed, it is now time to combine them in sorted order.

How to Write the Code for Merge Sort Algorithm?

Pseudo Code:

Now let’s understand the pseudo-code in detail:

1. The Divide Step

To divide the array into subarrays, we repeatedly do the following steps:

1. Store starting index as start and ending index as end.
2. If start<end:

• Find mid by using the formula: start+(end-start)/2
• Divide the left subarray i.e. index start to index mid
• Divide the right subarray i.e. index mid+1 to end

3. If end<start:

• return, as the entire array is traversed.

The above points will go in recursion and stop dividing when all elements become single array elements. The combined step is given below.

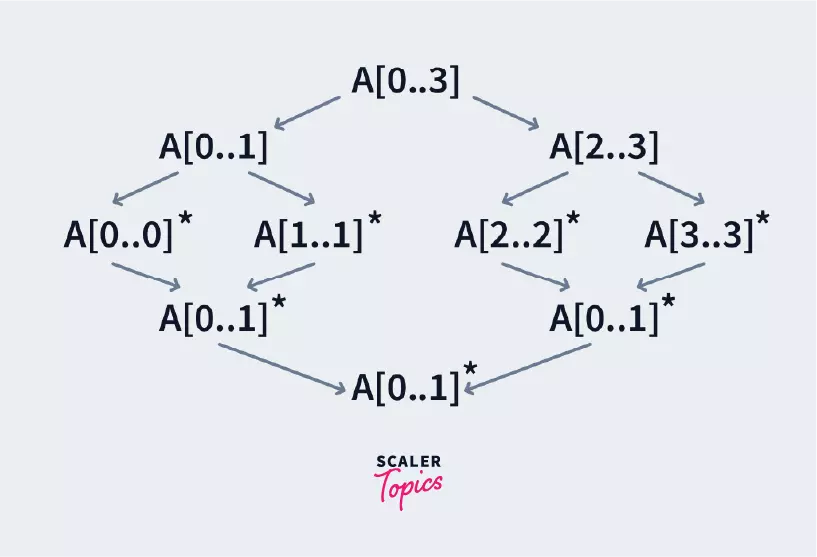
The Combine Step

To combine the 2 subarrays into one sorted array, we use 3 pointers. One is for traversing the first subarray, one for traversing the second subarray and the third one is for traversing the final sorted array. We do the following steps:

1. If any of the arrays have not been traversed entirely
   • Compare the first element of both arrays
   • Copy a larger element and put it in the final sorted array
   • Move the pointer of the subarray that consisted of the larger element.
2. If any of the arrays have been traversed entirely
   • Copy all remaining elements into a sorted array.

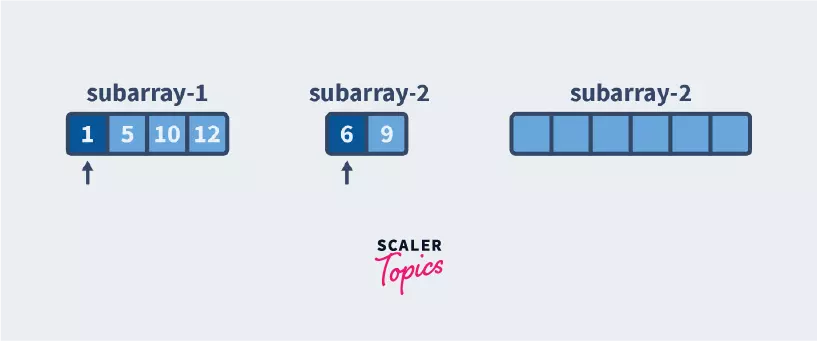
Step by Step Merge Function

Since we start combining when we have subarrays of length 1, when we get 2 subarrays to combine, they will be sorted amongst each other.

It is our job to sort these and put them together in the final sorted array. We accomplish this by having 3 pointers/references.

• At the beginning of the first subarray
• At the beginning of the second subarray
• At the sorted array

Until we reach the end of either of the subarrays, we keep checking which element is smaller and putting that in the array.

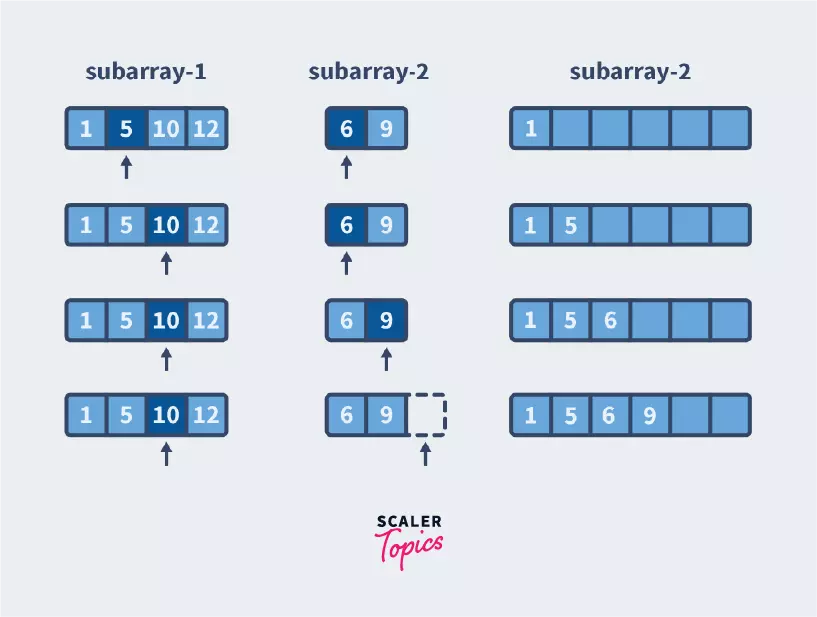
Here 1 is smaller, so we push that to the sorted array and then move the pointer of the subarray that contains 1 as the next number after 1 might be smaller or larger than 6 but the number after 6 is definitely larger than 1. We continue as follows:

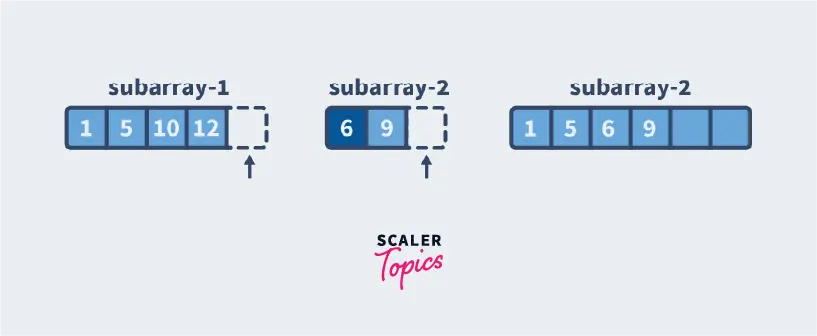
Now we see that we have reached the end of the second subarray. This means that the remaining numbers in the first sub-array are definitely larger and since they are sorted, we insert them in the final sorted array as-is.

Implementation of Merge Sort Algorithm

1. Merge Sort Code in Java

2. Merge Sort Code in Python

3. Merge Sort Code in C

4. Merge Sort Code in C++

5. Merge Sort Code in JavaScript

Time Complexity of Merge Sort Algorithm

Every time we divide a number in half, we may represent its time complexity using a logarithmic function, which is $\log_2(2)$. Let us see why this is done:

When n=2, $\log_2(2^1)$=1

When n=4, $\log_2(2^2)$=2

When n=8, $\log_2(2^3)$=3

• Now, this indicates that if we have an array of 8 elements, we will first divide it into an array of 4 elements.
• Then we will divide the array of 4 elements into an array of 2 elements. Then the array of 2 elements will be divided into single arrays.
• After which, the merge process will begin. From this, we can gather that the array can be divided 3 times. Although this will take us 4 steps, i.e. 8->4->2->1.
• $log_28$ which can be written as $\log_2(2^3)$, is giving us 3 which is the number of splits possible in the array.

We add 1 to determine the total number of splits. Hence the splitting process takes O($\log_2(n)$+1).

Then to find the middle element, it takes us O(1) time as we are just doing (start+end)/2.

Then to merge all the subarrays into a final sorted array, it takes us O(n) time, at max, as we need to traverse all elements of the array to determine the sorted order.

Hence, our total time complexity is O($\log_2(n)$+1)*O(1)*O(n).

Now O($\log_2(n)$+1) can be written as O($\log_2(n)$).

Hence, our time complexity is O(n*$\log_2(n)$).

Merge Sort’s time complexity is O(n*Log n) in worst case, average case, and best case, because it always divides the array into two halves and merges the two halves in linear time.

• Worst Case Time Complexity: O(n*$\log_2(n)$)
• Best Case Time Complexity: O(n*$\log_2(n)$)
• Average Case Time Complexity: O(n*$\log_2(n)$)
• Space Time Complexity: We require an additional array ‘sorted’ to store the final sorted array, hence the space-time complexity is O(n).

Drawbacks of Merge Sort Algorithm

The drawbacks of Merge Sort are as follows:

• We have seen that we need to store the sorted elements in a separate array of size n, this requires more space thereby increasing the space complexity.

• We have also seen that the pointers traverse through one entire sub-array. Let us consider the case where the subarrays are perfectly sorted.

For example subarray1={1,2,3} and subarray2={4,5,6}. The final sorted array looks like this {1,2,3,4,5,6} which is just subarray2 kept after subarray1 but we still need to traverse the entire array thereby wasting time.

• Merge Sort when considered for smaller arrays can prove to be slower as compared to other algorithms.

• Merge Sort Program in C++
• Merge Sort in C
• Time Complexity of Merge Sort