Priority Queue
Learn via video course

Overview
A priority queue is a special type of queue in which each element is associated with a priority value. And, elements are served on the basis of their priority. That is, higher priority elements are served first.
Takeaways
- Complexity of Priority queue
- Time complexity -
- Insertion :
- Peek :
- Deletion :
- Time complexity -
What is Priority Queue?
Consider a situation where you have 4 assignments, as of Monday:
- Database Management Systems, due on Thursday
- Statistics, due on Tuesday
- Data Structures and Algorithms, due on Wednesday
- Operating System, due on Friday

As a student, overburdened with work, if you do first come, first serve, you might not be able to submit all your assignments on time.
So instead, you assign a priority to each of them and get them done in that order. In this case:
- Database Management Systems, due on Thursday Priority Number 3
- Statistics, due on Tuesday Priority Number 1
- Data Structures and Algorithms, due on Wednesday Priority Number 2
- Operating System, due on Friday Priority Number 4


It is important to note that a priority queue only supports elements that are comparable. Elements are called comparable if they are either lesser than, equal to or greater than one another, i.e. if the two elements are a and b, they should follow one of the conditions:
i) a<b
ii) a=b
iii) a>b
As a result, the items in the priority queue are arranged in ascending or descending order.
It is an Abstract Data Type that functions a little differently than a normal Queue.
In a normal Queue, first-in-first-out is followed which means that whichever elements enters the queue first, will be the first to leave. Just like any queue we form, the person that stands first in the queue, will be addressed first and similarly, even in computer science queues, the same rule applies.
However, in a Priority Queue, each item in the queue is assigned a priority, and items are dequeued or removed based on this priority value assigned to them.
Hence, the items in the priority queue are arranged in either ascending or descending order depending on the priority value taken by the user. (in such a way that the highest priority elements are moved to the beginning of the queue and the lowest priority elements are moved to the back of the queue).
Characteristics of a Priority Queue
A queue is called a Priority Queue when it has the following characteristics:
- Each item in the queue must have a priority associated with it.
- Higher or lower priority elements must be dequeued before lower or higher priority elements respectively depending on priority order taken by user that is if user consider lower number as higher priority or higher number as higher priority.
- If two elements in the queue have the same priority value then the first in first out rule is followed for these two elements alone i.e. the element that entered the priority queue first will be the first to be removed.
Types of Priority Queue
There are two types of Priority Queues:
1. Ascending Order Priority Queue
As mentioned before, the elements in the priority queue must be comparable which means they are either less than, equal to or greater than one another. In an ascending order priority queue, all the elements are compared with another and the rule:
The smaller the element(number), the higher the priority is applied.
Let us consider a priority queue having the following priorities:
4,2,6,1,8
The first step would be to arrange them in ascending order as follows:
1,2,4,6,8

In this priority queue, 1 is the smallest number and is hence the item with the highest priority. On the other hand, 8 is the largest number and is hence the item with the lowest priority.
2. Descending Order Priority Queue
In a descending order priority queue, all the elements are compared with another and the rule:
The larger the element(number), the higher the priority.
Let us consider a priority queue having the following priorities:
4,2,6,1,8
The first step would be to arrange them in descending order as follows:
8,6,4,2,1

In this priority queue, 8 is the largest number and is hence the item with the highest priority. On the other hand, 1 is the smallest number and is hence the item with the lowest priority.
Implementation of Priority Queue in Data Structures
A Priority Queue is implemented using one of the 4 Data Structures:
1. Linked List
In the linked list, the element having higher priority will be present at the head of the list. Then, based on priority, all the elements in the list are arranged in descending order based on priority.
Class Declaration:
To insert an element, the list is traversed until a suitable position is found for the element to be inserted in order to maintain the overall order of the linked list. Hence, the worst time complexity is O(n) as the worst case is when all elements of the list need to be traversed.
For example, let us consider the linked list:

Let us consider that we need to insert an element with priority 8. 8 has a priority lower than 5 so we traverse the linked list till we find a position where it is suitable. The linked list will then look like this:

For deletion, the highest priority element will be removed first from the priority queue and the highest priority element is at the head of the list and hence it will simply be removed.
peek() is used to retrieve the highest priority element without removing it and this is also present at the head of the list.
Since the highest priority element is present at the head of the list, it takes just O(1) time to remove it or to do the peek() operation.
2. Binary Heap
This is the most efficient implementation of a Priority Queue.
The top priority element is present at the root node of the heap and hence the peek operation has a time complexity of O(1). Insertion and Deletion operations using Heap are illustrated in the next section. For insertion and deletion, the heapify operation must be done and hence the time complexity for the same is O(log n) each.
3. Arrays
There are two ways to go about implementation of priority queues using arrays. The first is to use an ordered array and the other is to use an unordered array. In an ordered array, all the elements are ordered according to priority.
To insert a new element, you must traverse the array and insert it in such a way that the ordering is maintained. The worst case is hence O(n). Since they are in order, both the delete and the peek operations take O(1) time.
In an unordered array, all the elements are not arranged according to priority. Hence to insert an element, it does not matter where you insert it and hence it takes O(1) time.
However, to do the delete and peek operation, you must traverse the array and hence, the worst-case time complexity is O(n) for both.
4. Binary Search Tree
To maintain items efficiently in sorted order, a binary search tree is utilised. The binary search tree becomes a priority queue if the sort order is based on priority.
The time complexity to locate the top priority element is constant.
We can keep an extra pointer to store the highest priority element, which will be updated as the insertion and deletion operations are completed. We will update the additional pointer with the deletion action by identifying the inorder successor.
Why are Heaps preferred over Binary Search Trees?
- Heaps can be constructed in O(N) time, however, the Self Balancing BST takes O(nLogn) time.
- Heaps are implemented using arrays, so the pointers don’t take up any more space.
Table for time complexities to implement priority queue using various data structures:
| Data Structure | Insert | Delete | Peek | Reason |
|---|---|---|---|---|
| Linked List | O(n) | O(1) | O(1) | Highest priority element at head and hence can be removed in O(1) time. For insertion, list needs to be traversed till suitable position found, hence O(n). |
| Ordered Array | O(n) | O(1) | O(1) | All elements in order since remove and peek are O(1). For insertion, the array must be traversed until a suitable place is found, hence O(n). |
| Unordered Array | O(1) | O(n) | O(n) | In an unordered array, insertion can be done anywhere since no order is maintained hence O(1). However for removal or peek, the list must be traversed to find the highest or lowest priority element, hence O(n) |
| Heap | O(log n) | O(log n) | O(1) | Top priority or lowest priority element is present at the root node and hence the complexity for peek is O(1). For removal and insertion, heapify operations must be implemented which takes O(log n) complexity. |
| Binary Search Tree | O(log n) | O(log n) | O(1) | A pointer can be kept at the highest or lowest priority element and hence the time complexity for peek is O(1). For both insertion and deletion operations, the tree must be brought back to a form where all binary search trees conditions hold true and hence the time complexity is O(log n). |
Priority Queue Operations
The operations on a Priority Queue in a heap are done in the following way:
A heap is a tree based data structure. A max-heap is one where the key value of the parent node is always greater than or equal to the key value of the child node. Hence, the element with the largest key value comes at the root.
Conversely, a min-heap is one where the key value of the parent node is always lesser than or equal to the key value of the child node. Hence, the element with the lowest key value comes at the root.
1. Inserting
We will make use of the Max-Heap data structure to implement insertion in a Priority Queue. The algorithm is as follows:
- START
- If(no node):
- Create node
- Else:
- Insert node at end of heap
- Heapify
- END
Let us now see with an example how this works:
Let’s say the elements are 1,4,2,7,8,5. The max-heap of these elements would look like:
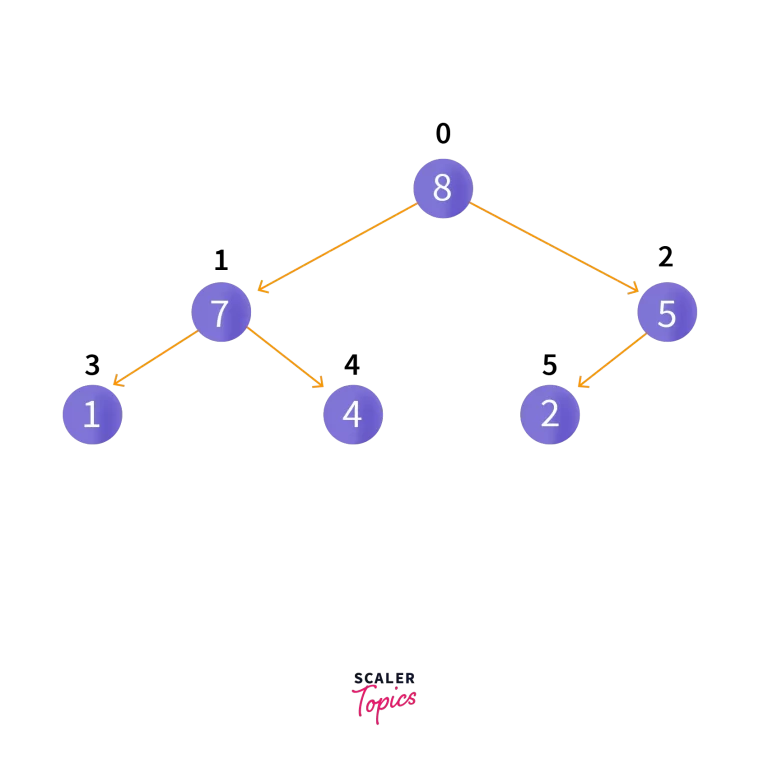
Now, let’s try to insert a new element, 6. Since there are nodes present in the heap, we insert this node at the end of heap so it looks like this:
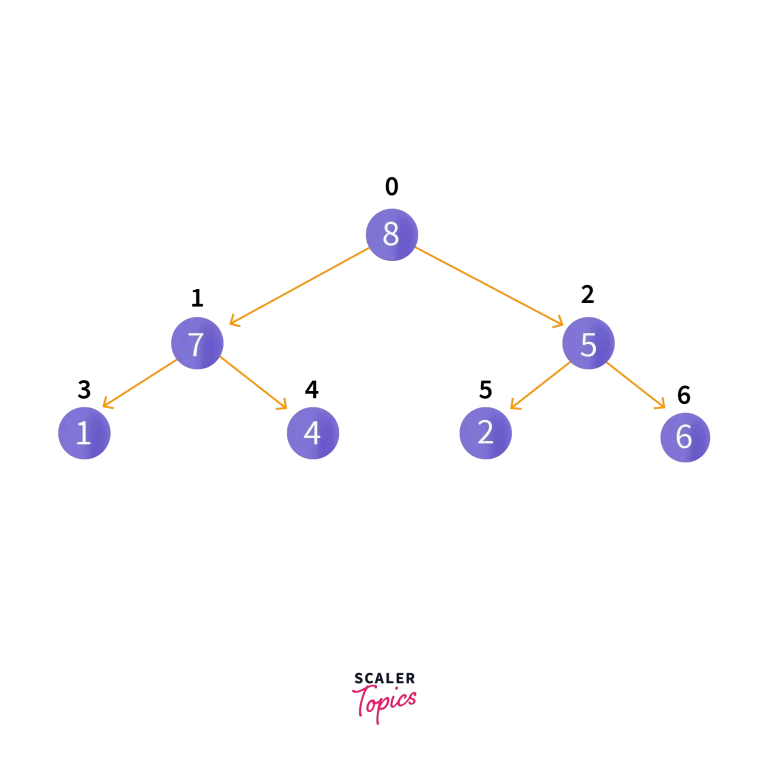
Then, heapify operation is implemented. After which, the heap will look like this:
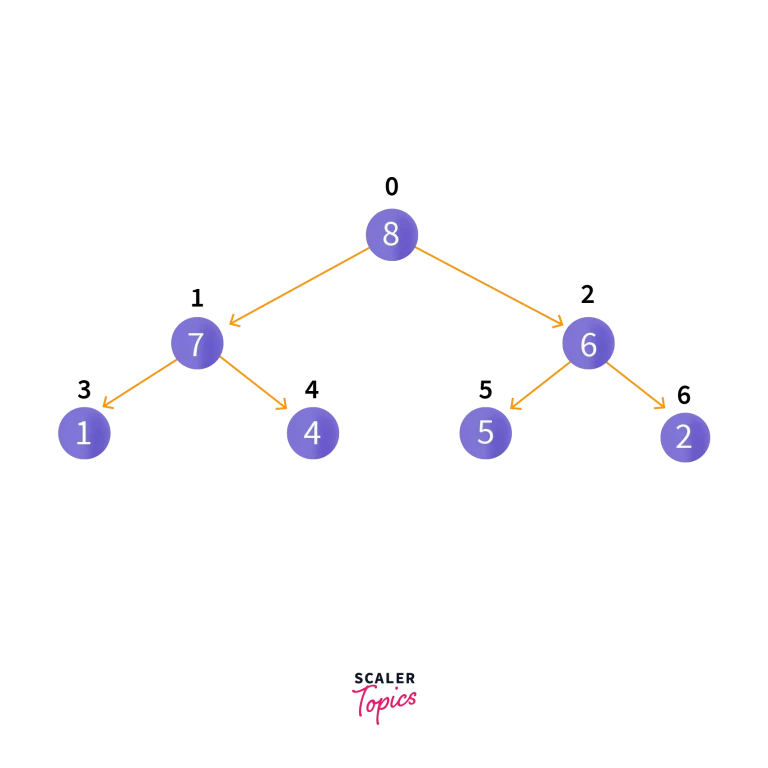
2. Deleting
We again make use of the Max-Heap Data Structure here to implement deletion in a Priority Queue. The algorithm is as follows:
- START
- If node that needs to be deleted is a leaf node:
- Remove the node
- Else:
- Swap node that needs to be deleted with the last leaf node present.
- Remove the node
- Heapify
- END
Let us now see with an example how this works:
Let’s say the elements are 1,4,2,7,8,5,6. The max-heap of these elements would look like:
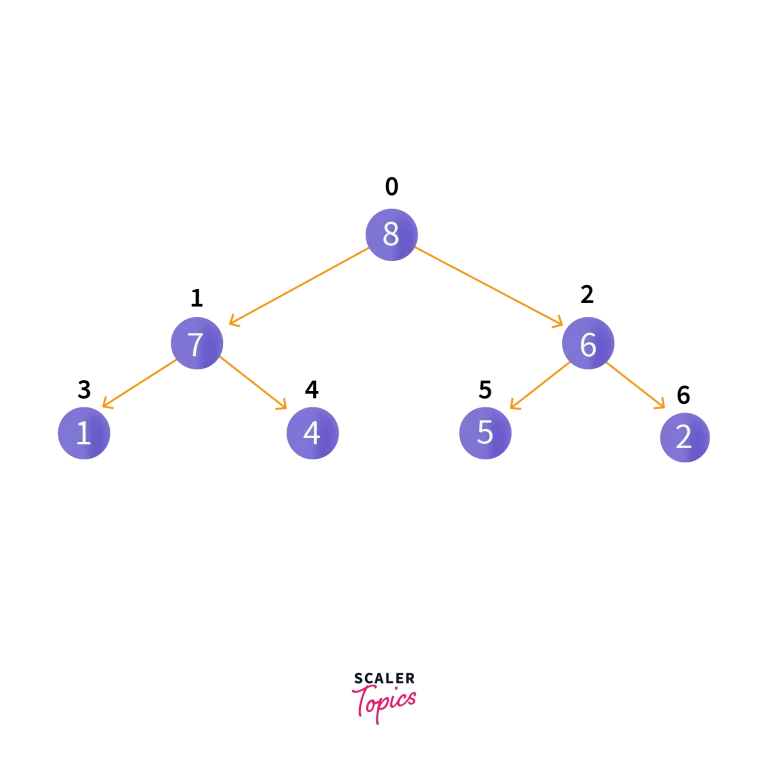
Now, let’s try to delete an element, 6. Since this is not a leaf node, we swap it with the last leaf node so it looks like this:
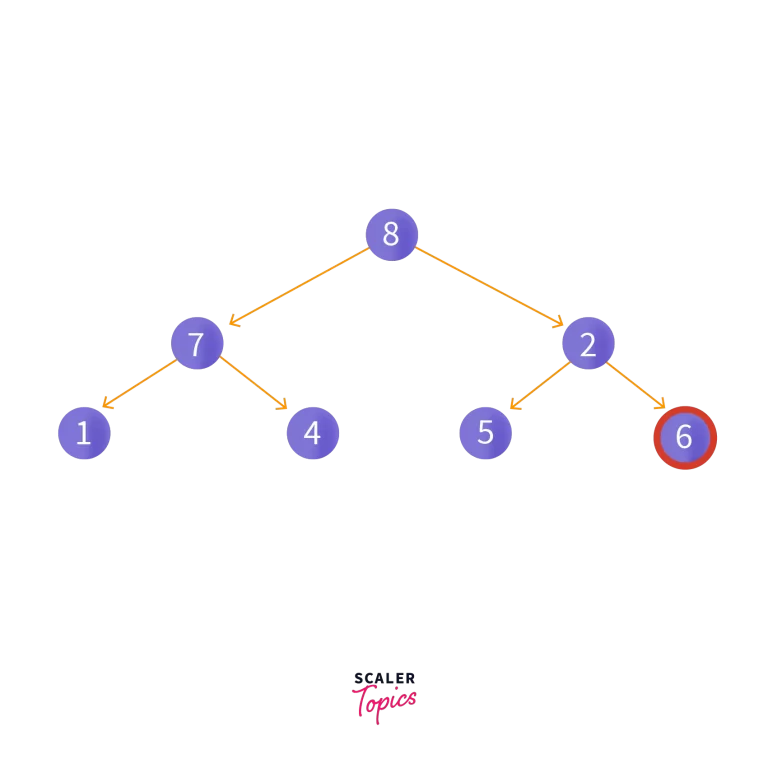
Then, we remove the leaf node so it looks like this:
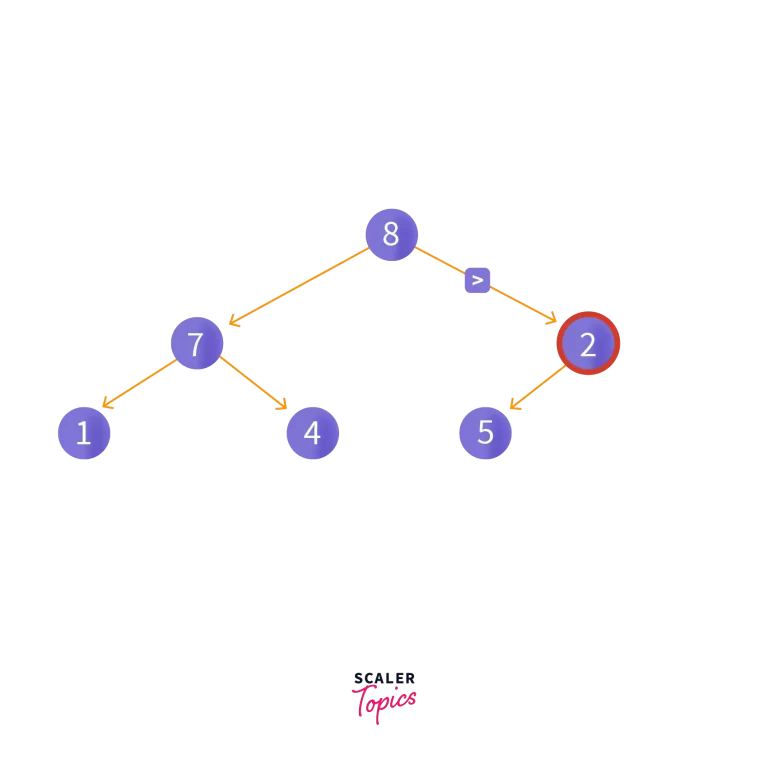
Then, heapify operation is implemented. After which, the heap will look like this:
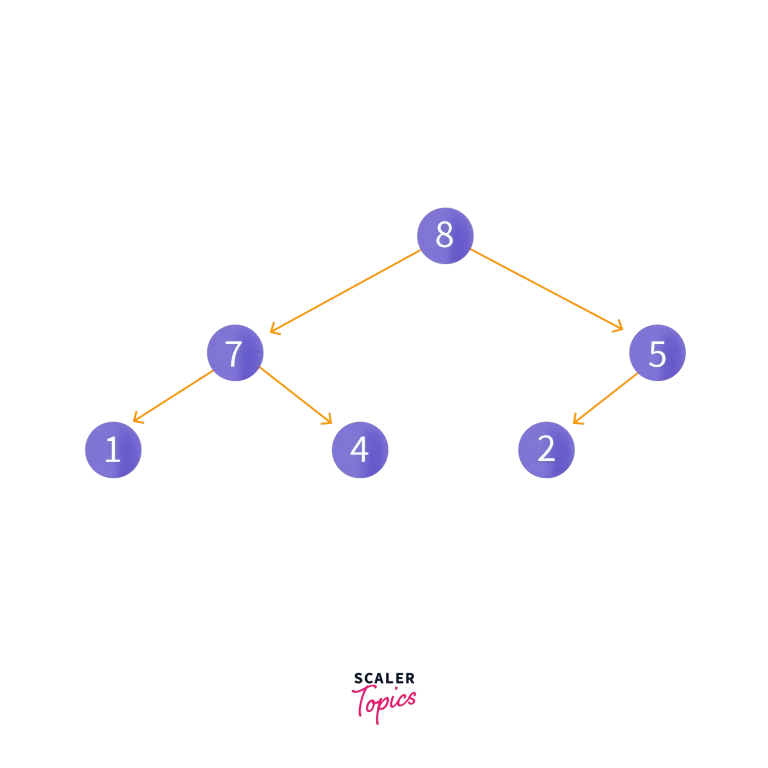
a. Peeking from the Priority Queue
This will return the maximum element if a max-heap is used and the minimum number if a min-heap is used.
To do both of these, we return root node. This is because in the max-heap or the min-heap the maximum or minimum element will be present at the root node respectively.
b. Extract-Max/Min from the Priority Queue
This also returns the maximum element if a max-heap is used and the minimum number if a min-heap is used.
However, in this case, the maximum/minimum element will also be removed from the heap data structure. It hence returns the maximum or minimum after extracting or removing it from the heap.
Priority Queue Implementations in Python, Java, C, and C++
Implementation in Python:
Output:
Implementation in Java
Output:
Implementation in C++
Output:
Application of Priority Queue
The following are the applications of a Priority Queue:
- It is used in Djikstra’s Algorithm – To find the shortest path between nodes in a graph.
- It is used in Prim’s Algorithm – To find the Minimum Spanning Tree in a weighted undirected graph.
- It is used in Heap Sort – To sort the Heap Data Structure
- It is used in Huffman Coding – A Data Compression Algorithm
- It is used in Operating Systems for:
- Priority Scheduling – Where processes must be scheduled according to their priority.
- Load Balancing – Where network or application traffic must be balanced across multiple servers.
- Interrupt Handling – When a current process is interrupted, a handler is assigned to the same to rectify the situation immediately.
- A* Search Algorithm – A graph traversal and a path search algorithm
Apart from that a Priority Queue can also be used in real life in situations where priority must be established for example, a hospital. There is a queue that’s followed, however, if an emergency case comes to the hospital, they must be dealt with first and hence move to the front of the queue due to their priority.
Conclusion
The Priority Queue is an important data structure to solve any question that wants you to handle things that have different priorities.
The major advantage of using a priority queue is that you will be able to quickly access the highest priority item with a time complexity of just O(1).
The only disadvantage of using Priority Queues are that the enqueue and dequeue operations are slow and have a time complexity of O(log n). A few important coding questions that make use of Priority Queue are ‘Connect n ropes with minimum cost’ and ‘Top k frequent keywords’.
