Quick Sort Algorithm

Introduction

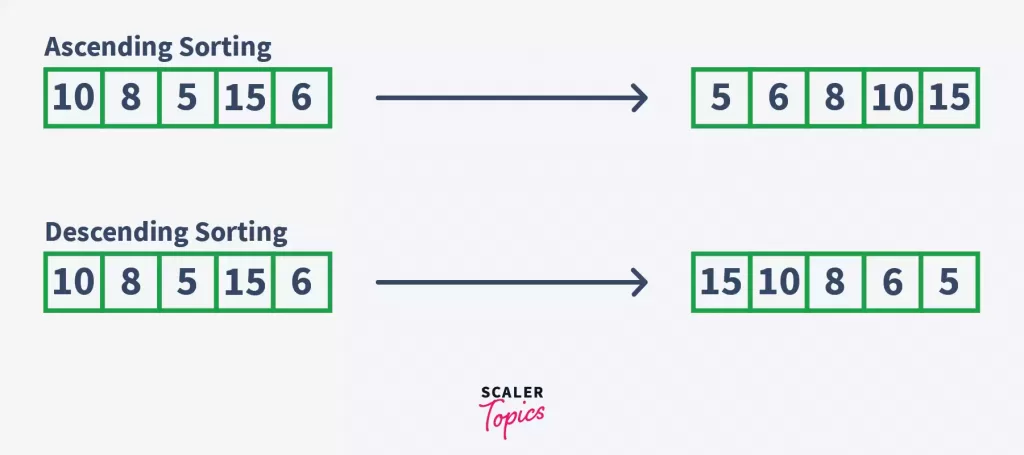
Consider a list with the elements – 10, 8, 5, 15, 6 in it. We have to arrange these elements in both ascending and descending order.

How are we going to perform this arrangement? Simple answer – by using a Sorting algorithm.

A sorting algorithm is a method of reorganizing the elements in a meaningful order. In both the above-given examples, we have implemented a sorting algorithm to get the desired results.

There are multiple algorithms that can be used for sorting. And, in this article, we will discuss Quick sort.

What is Quick Sort?

Quick sort, also known as partition-exchange sort, is an in-place sorting algorithm. It is a divide-and-conquer algorithm that works on the idea of selecting a pivot element and dividing the array into two subarrays around that pivot.

In quick sort, after selecting the pivot element, the array is split into two subarrays. One subarray contains elements smaller than the pivot element, and the other subarray contains elements greater than the pivot element.

Below given is a representation of what the input array looks like after the first iteration –

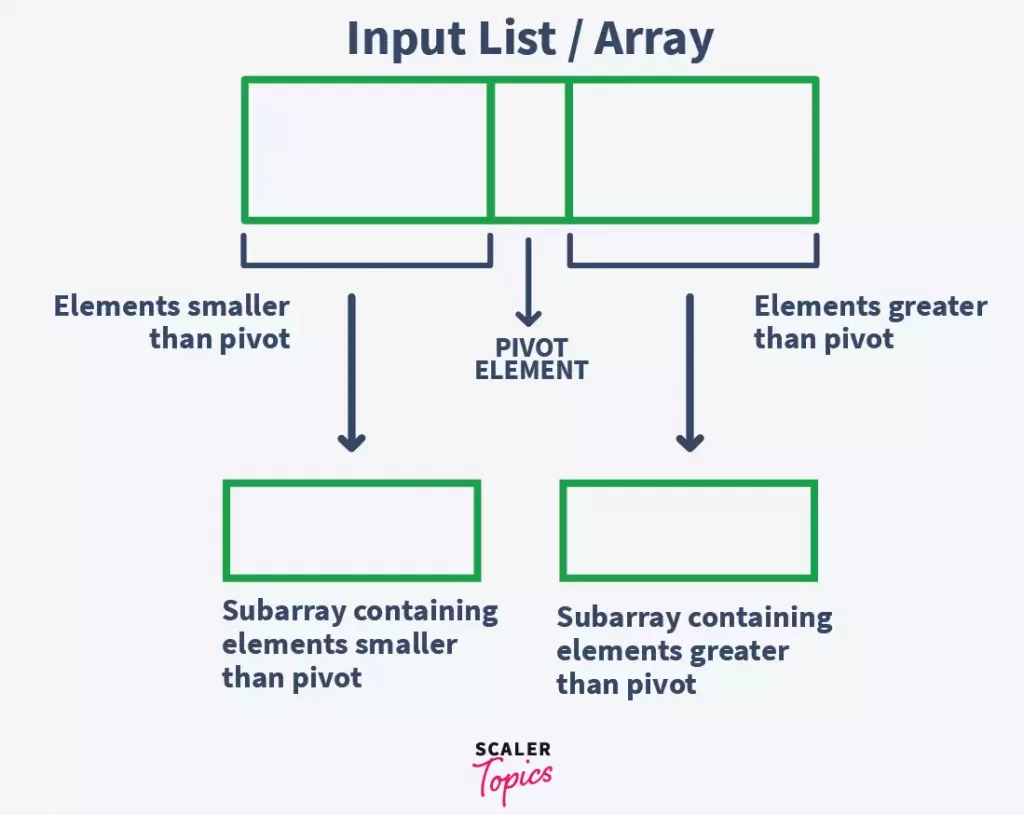
At every iteration of quick sort, the chosen pivot element is placed at its correct position that it should acquire in the sorted array. This makes sure that each chosen pivot element is at its correct sorted position.

This process of selecting the pivot element and dividing the array into subarrays is carried out recursively until all the elements in the array are sorted. In other words, each subarray is divided further until each subarray consists of only one element. All these subarrays are then combined to form a single sorted array. Since we know before partitioning of the array, the pivot is placed at its correct position, dividing the array to one single element places each element at its correct sorted position, and thus, combining all of them gives us a sorted array.

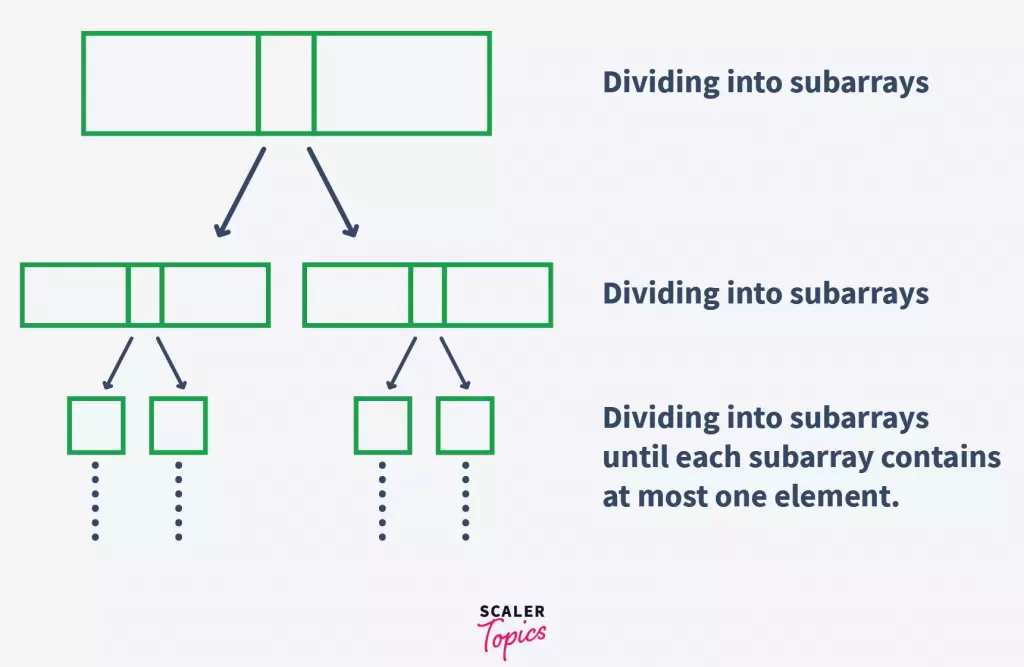
This way, with each iteration of, the problem reduces by 2 steps making quick sort a faster way to sort an array.

One interesting thing to note here is that we can choose any element as our pivot, be it the first element, the last element, or any random element from the array.

To better understand the quick sort algorithm, imagine this. Owing to your good conduct, your class teacher gives you the responsibility of a monitor. One day, for a fest, your teacher calls you up and asks you to help her in arranging the students in height-wise order.

There are many ways in which you can arrange the students, you can pick every student and show them their places one by one, but this would take too much time if there are a lot of students (say 500), and you have to finish your job as soon as possible. So, one of the fastest ways could be asking the students to arrange themselves.

For example, the shortest student knows that he has to stand at the front. Same for the tallest student and the students with medium height.

In this way, every student can find his/her correct position by comparing his/her height with that of students before and after him/her.

Similarly, in quick sort, every element arranges itself at its correct position to sort the given array. Here, the pivot element is placed at its correct sorted position, and hence it is the element that we know is definitely sorted. And thus, subarrays are divided around the pivot element.

Furthermore, our Data Structures and Algorithms course extensively covers sorting algorithms, including Quick Sort. In Quick Sort, each element rearranges itself to its correct position within the array, ensuring a sorted outcome. The pivot element plays a crucial role as it is placed in its correct sorted position, serving as a reference point for dividing the subarrays.

Working of Quick Sort Algorithm

Recall the list/array that had the elements – 10, 8, 5, 15, 6 in it. To sort these elements in ascending order using quick sort, let us follow the under-given steps –

Step – 1:

Select the pivot element, here for the sake of simplicity, we are selecting the rightmost element as the pivot.

Step – 2:

Rearrange the elements of the array in a way that all the elements smaller than the pivot are on its left and that all the greater ones are on the right. They need not be sorted. After the rearrangement, the array would look like this –

Here, 6 is our pivot element, and all the elements greater than itself are on the right side, while the elements smaller than the pivot is on its left side.

Now let us understand how did this rearrangement happen –

• Take two pointer variables that point to the left & right of the array (with pivot excluded). Let’s call them left & right respectively.

• Under a loop, increment the left pointer until a value greater than pivot is found. In this case, since 10 is already greater than 6, we move to step c.

• Under the same loop, increment the right pointer until a value smaller than pivot is found. Here, a value smaller than pivot is 5.

• Now since the conditions given in steps b and c are simultaneously fulfilled, swap the value at index left with the value at index right of the given array. This helps us move the elements smaller than the pivot element to the left of it, and the greater ones to the right of it. Here, 5 & 10 are swapped.

• Repeat steps b, c and d until the left index is greater than the right index.

• Here, the execution of the loop is stopped because left > right. Now, swap the value at pivot with the value at the index left or right. 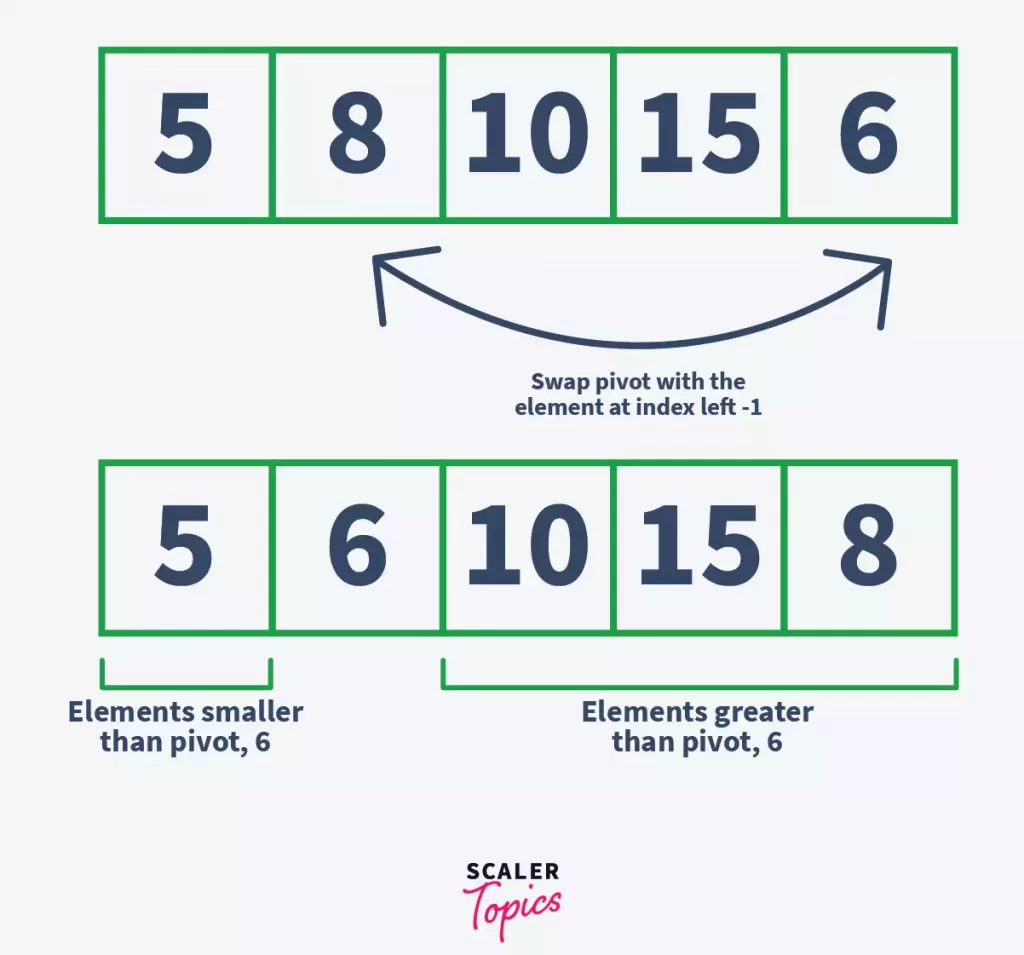We have placed 6 after 5, and before 10, 15, and 8. This way, we have placed 6 (pivot element) at such a position that elements smaller than it is on its left, and the elements greater than it is on its right. Notice that 6 is at its correct sorted position now.

Step – 3:

In this step, the sublist is divided into two parts – sublist before the pivot element, and sublist after the pivot element.

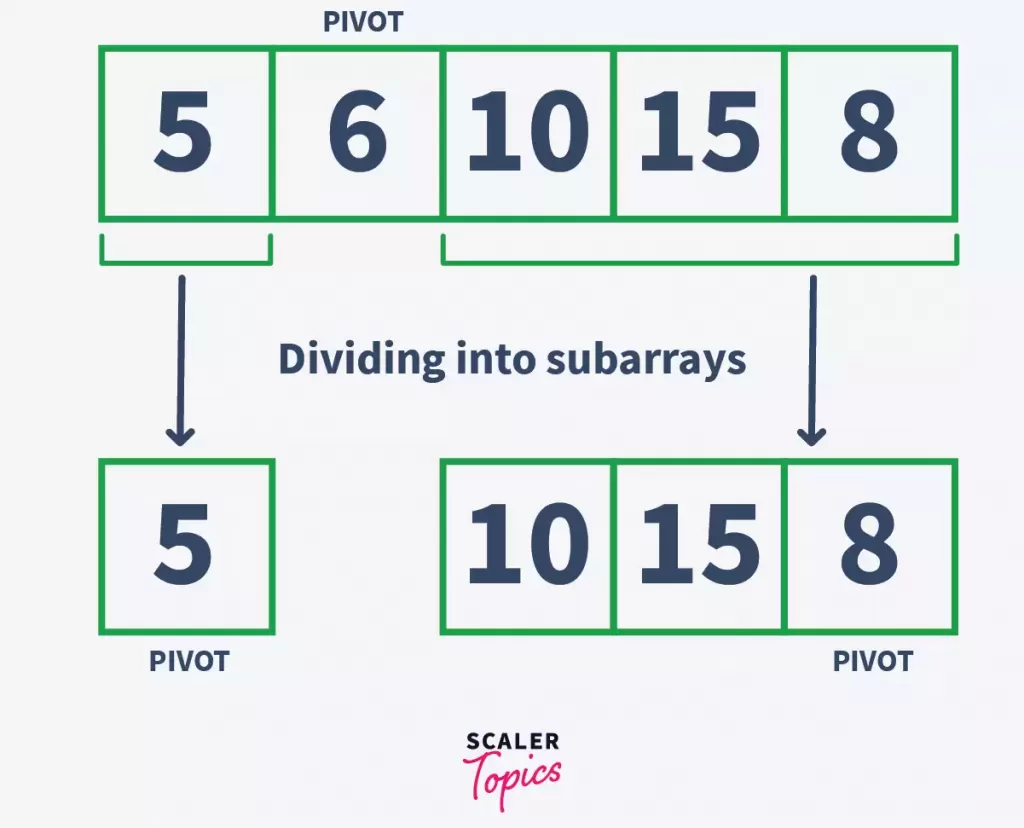
Step – 4:

Repeat the above-given steps recursively until all the elements of the array are at their correct sorted position.

The following diagram shows the working of the quick sort algorithm.

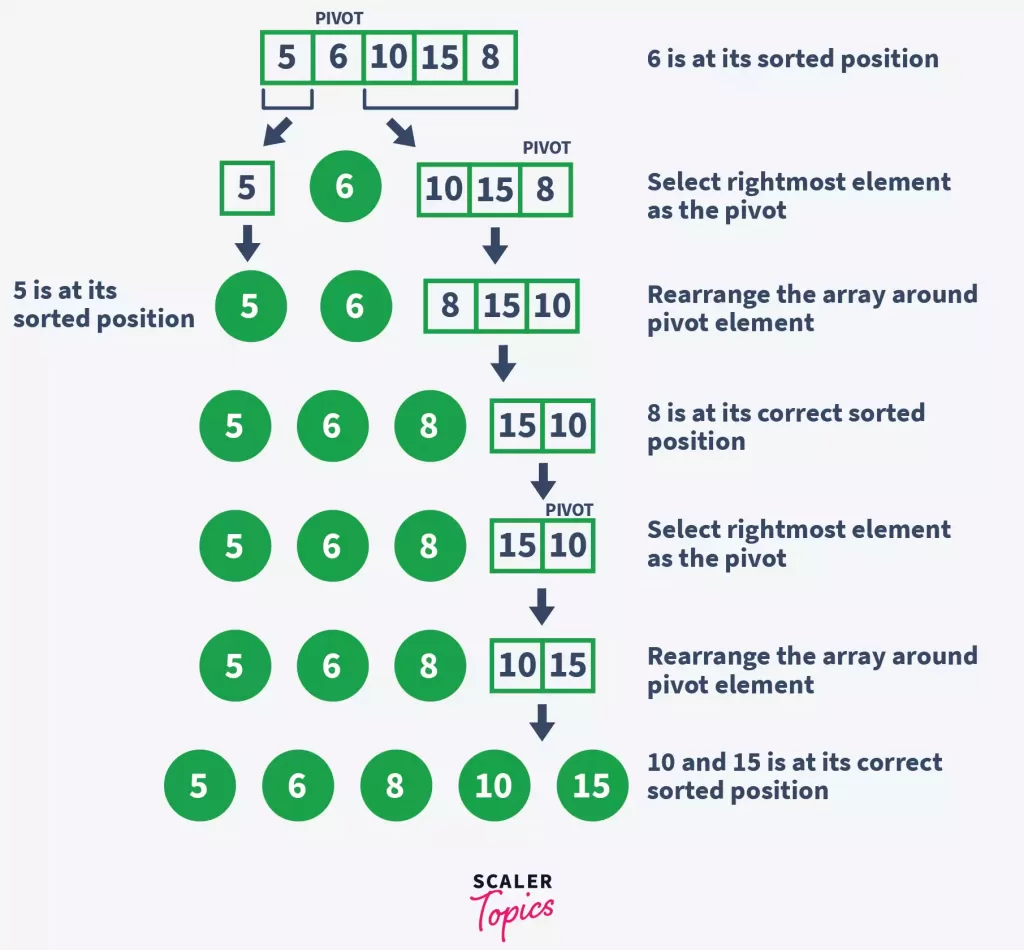
We have sorted the array using the quick sort algorithm. Let’s write some code to implement the algorithm.

Pseudocode for Quick Sort Algorithm

1. Pseudocode for Partitioning/Creating Subarrays –

2. Pseudocode for Quick Sort Function

Implementation of Quick Sort

1. C Program for Quick Sort

2. C++ Program for Quick Sort

3. Python Program for Quick Sort

4. Java Program for Quick Sort

Complexity Analysis of Quick Sort

1. Quick Sort Time Complexity

Best-Case:

The best-case occurs when the pivot is almost in the middle of the array, and the partitioning is done in the middle. So, let us assume that we have a total of n elements in the array, and we are dividing the array from the middle.

In this case, with each partition, we will have at most n/2 elements. And we have to perform the partition until only one element is left in each subarray. The following is the tree representation of the given condition

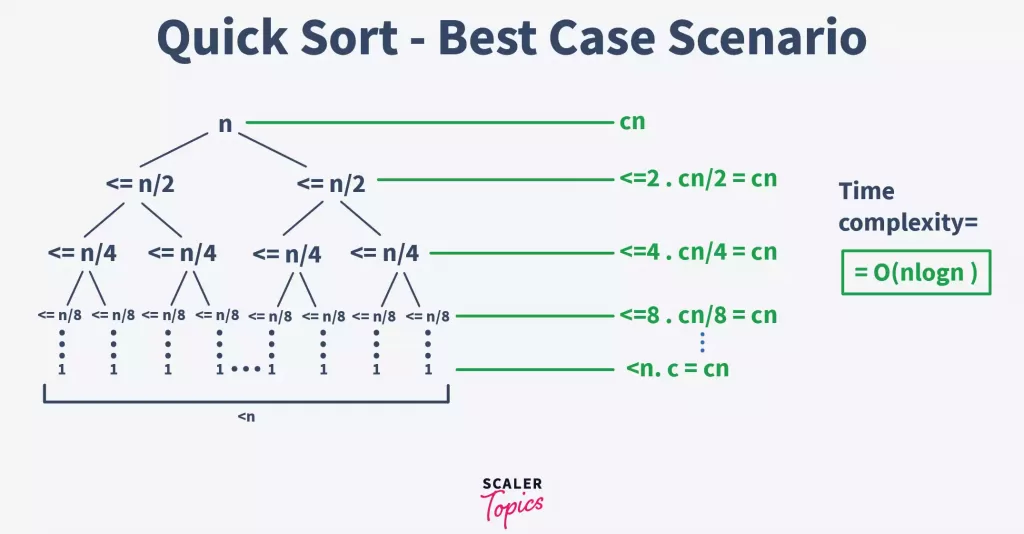
Notice that the above-given tree is a binary tree. And for a binary tree, we can know that its height is equal to logn. Therefore, the complexity of this part is O(logn).

Also, the time complexity of the partition() function would be equal to O(n). This is because, under the function, we are iterating over the array to swap rearranging the array around the pivot element.

Therefore, from the above results, we can conclude that the best-case time complexity for the quick sort algorithm is O(nlogn).

Worst Case:

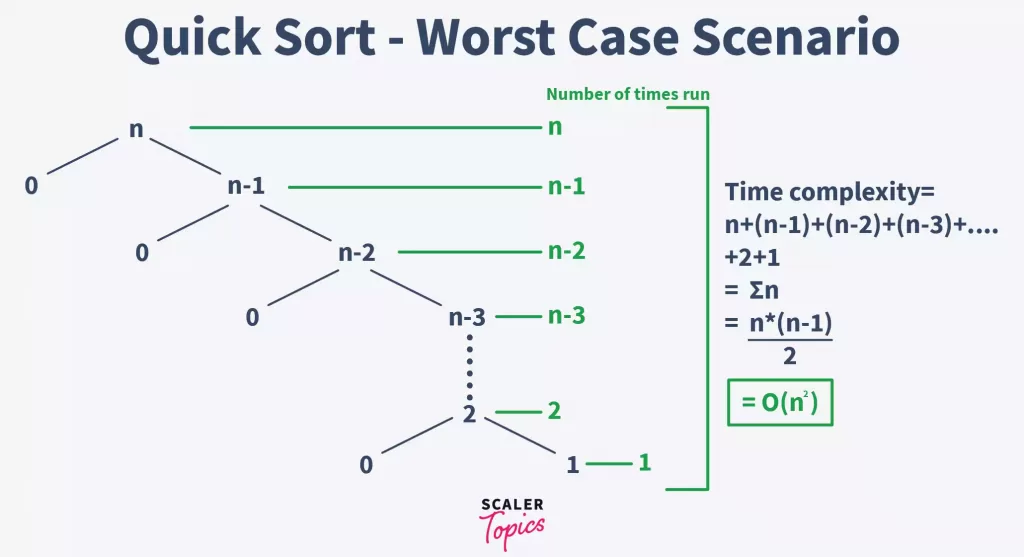
The Worst-case occurs when either of the two partitions is unbalanced. This generally happens when the greatest or smallest element is selected as the pivot.

In this case, the pivot lies at the extreme of the array, and one subarray is always empty while the other contains n – 1 elements.

This way, in the first call, the array is divided into two subarrays of 0 & n – 1 elements respectively. For the second call, the array with n – 1 elements is divided into two subarrays of 0 & n – 2 elements respectively. This continues till only one element is left.

The time complexity, in this case, would be the sum of all the complexities at each step.

T(quicksort) = T(n) + T(n – 1) + T(n – 2) + …….. + 2 + 1

T(quicksort) = O((n * (n – 1))/2)

T(quicksort) = &O(n ^ 2)&

The following is the tree representation of this condition –

2. Quick Sort Space Complexity

In quick sort, the time complexity is calculated on the basis of space used by the recursion stack. In the worst case, the space complexity is O(n) because in the worst case, n recursive calls are made. And, the average space complexity of a quick sort algorithm is equal to O(logn).

FAQs

1. Where is Quick Sort Used?

• Quick sort is used in separating Nth smallest or the largest element from an array.
• Being a fast sorting algorithm, quick sort is used by various departments in information retrieval.
• It is used for numerical computing where the efficient algorithms use priority queues and in turn quick sort for achieving accuracy.
• It is used where fast searching and/or sorting is the priority.

2. Is Quick Sort a Stable Algorithm?

An algorithm is called stable if the relative order of two equal elements is preserved. Therefore, quick sort is not a stable algorithm because ordering is done on the basis of the pivot’s position.

3. Why Quick Sort Runs Faster Than Merge Sort?

Quick sort is an in-place algorithm. But in merge sort, a new temporary array is required to merge the sorted subarrays. Therefore, quick sort is faster than merge sort.

Moreover, in quick sort, the worst case can be avoided by randomly choosing an element as the pivot, and performing sorting around it. Thus, a properly implemented quick sort has a time complexity of O(nlogn) in the average case.

4. Why Quick Sort is Preferred for Array?

Quick sort is cache-friendly, which means it does not create unnecessary buffers in the cache memory and slows the system down. It is because, when used for arrays, quick sort has a good locality of reference

Learn More

• Quick Sort in C
• Quick Sort in C++
• Quick Sort in Java