Types of Trees in Data Structures
Learn via video course

Overview
The tree data structure is a non-linear data structure that resembles a real-life tree, except, up-side-down. It has the root at the top and leaves at the bottom. It comprises entities known as "nodes" and "edges". The diagram below represents a tree.

The tree data structure is essentially a hierarchical data structure that stores information in a hierarchical manner i.e. every node has multiple other nodes connected to it on the next level called children. A tree is a data structure that has relationships between the node entities - parent-child relationships.
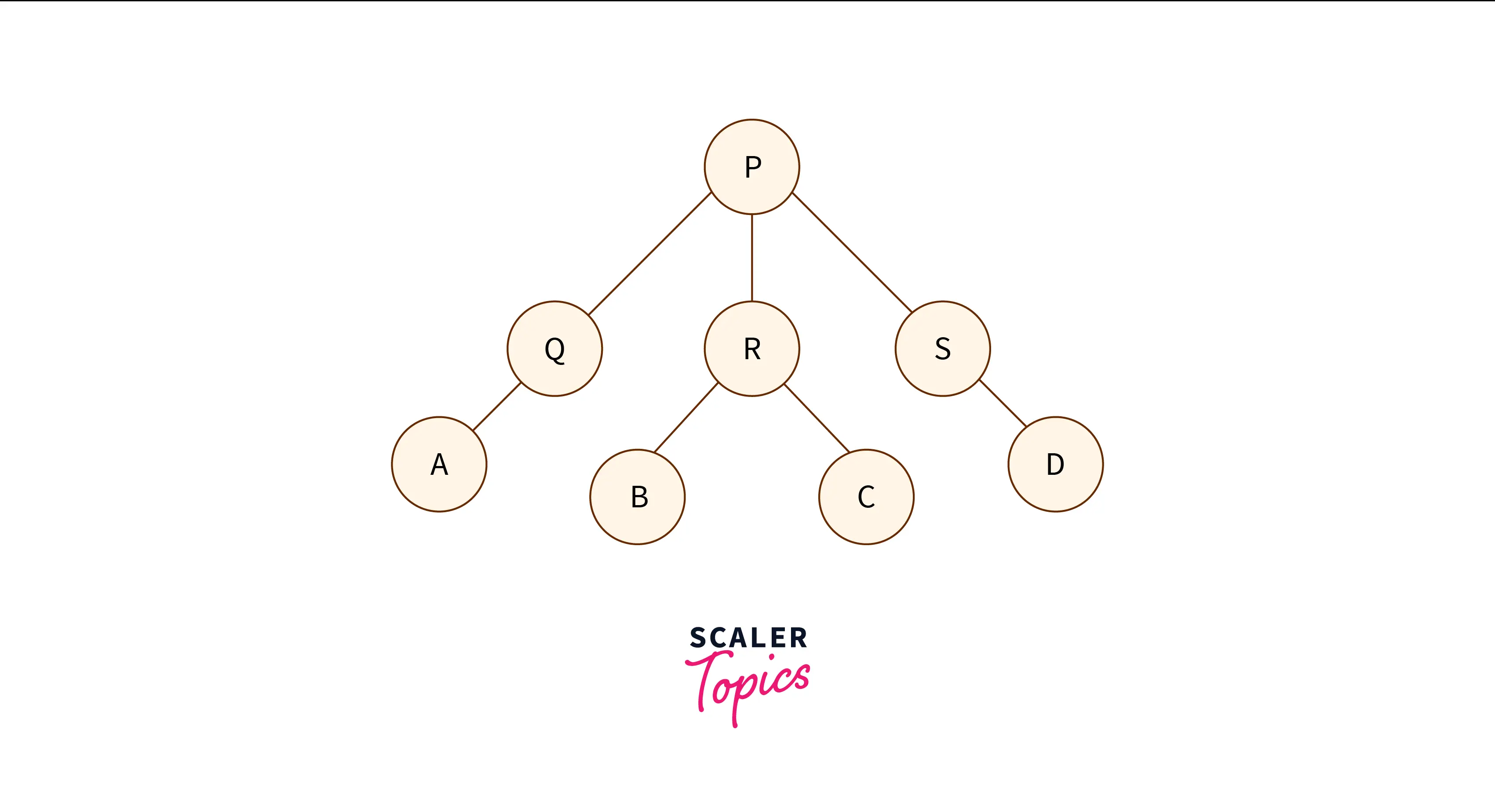
In the above diagram, the root node is "P" and is also a parent since it has more nodes below it. The child nodes of P are - Q, R, and S. Similarly, the child of Q is A, and so on.
Scope
- This article is a cheat sheet for all the types of trees in data structures. It contains the most important points related to the types of trees for revision purposes.
- This article does not contain an in-depth explanation of trees of any type or any code related to them.
Cheatsheet for Types of Trees in Data Structure
In the following sub-topics, you will be able to revise all your concepts related to the tree data structure and its types. Some important definitions and terminologies related to the tree data structure:
-
Node: A data containing element that maintains links to its children / parents. It is also known as vertex.
-
Edge: The connections between nodes/vertices.
-
Root: The first node of the tree, or the top node is the root node. It is the only node without a parent.
-
Parent: It is the node that is connected to another node while moving upwards, toward the root. This parent node would be the immediate parent.
-
Child: When moving away from the root, it is the node connected to another node.
-
Leaf: A node is said to be a leaf node if it doesn't have any children.
-
Subtree: A subtree of a tree T, is the tree that contains all the children nodes of a node in tree T, and well as the descendants.
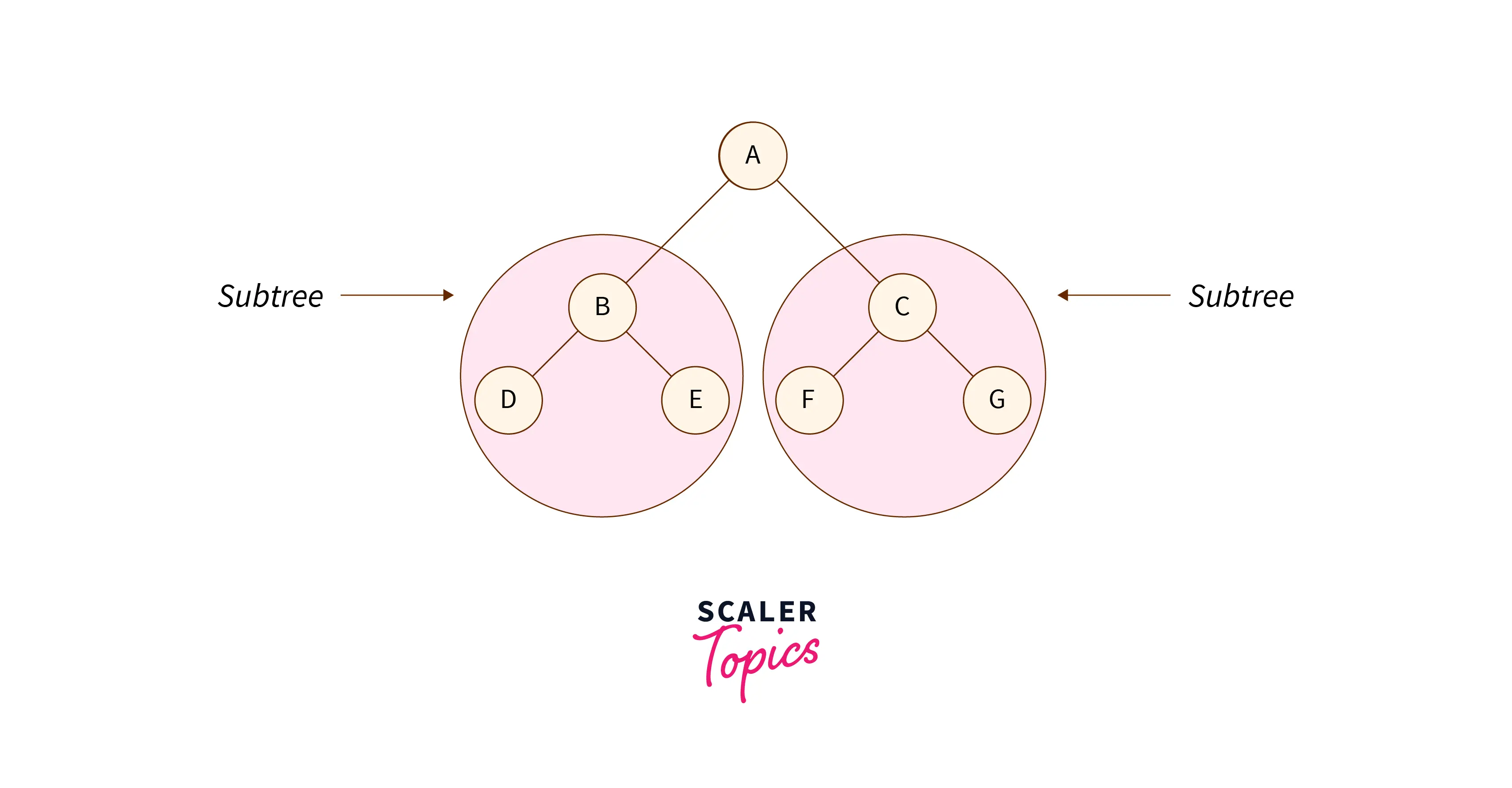
-
Degree: The degree of a node is defined as the number of subtrees of that node.
-
Depth: Depth of a node is defined as the number of edges from the current node to the root node of the tree.
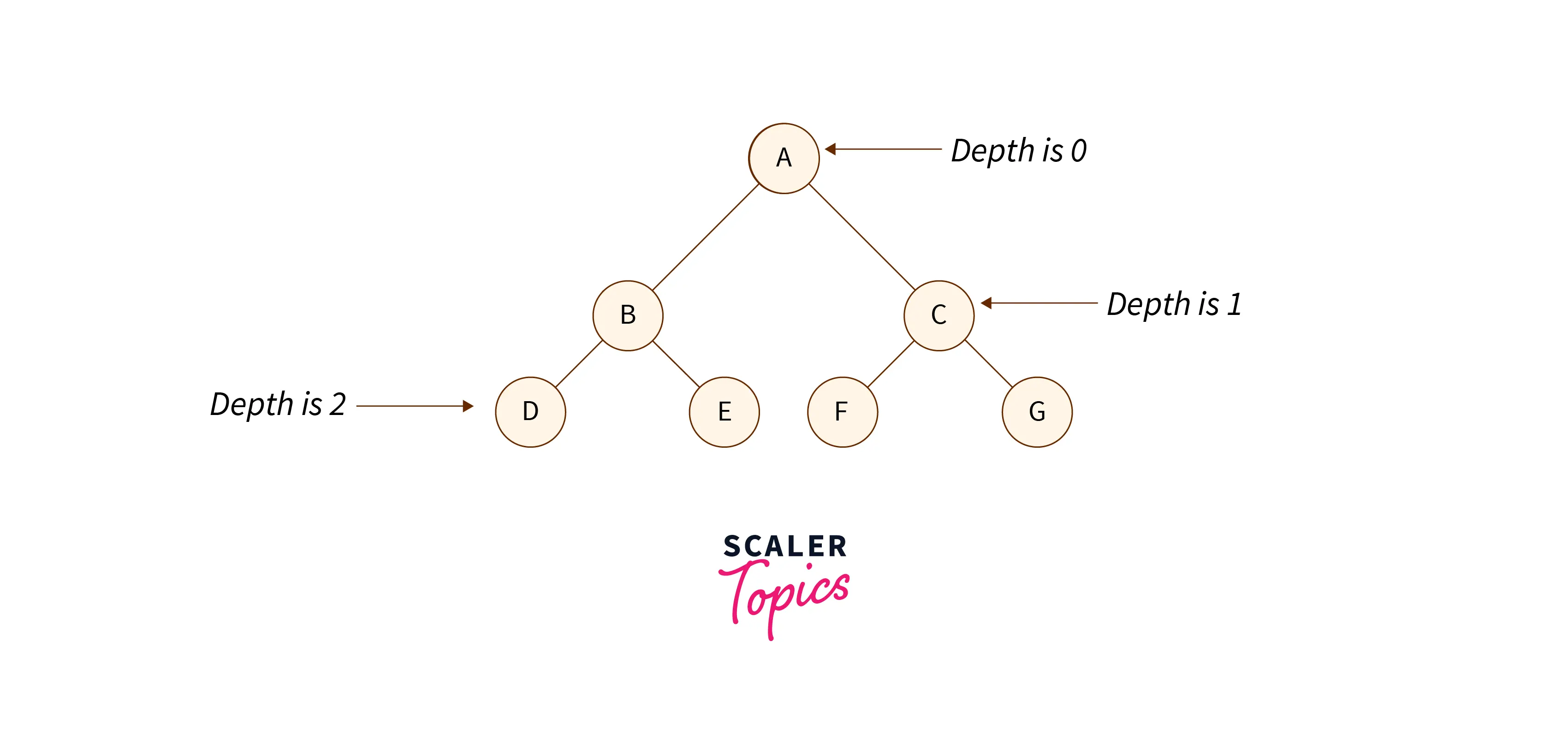
-
Level: In a tree, the root node is said to be at level 0, the children of the root node are said to be at level 1 and the children of nodes at level 1 are at level 2 and so on.
-
Height: Height of a tree is defined as the number of edges from the leaf node to the root node.
Note: To understand the different between the height and depth of a tree, you can take the analogy of the human body or the ocean. To measure someone's height, you do it from toe to head i.e. from leaf to root. However, if you want to measure the depth of the ocean, you do it from the surface of the earth to the bed of the ocean i.e. root to leaf. Adding on to that, for some internal node of the tree, the depth of the node is essentially how many levels it is beneath the root node. It's height, however, is how many levels it is above it's bottom-most child node.
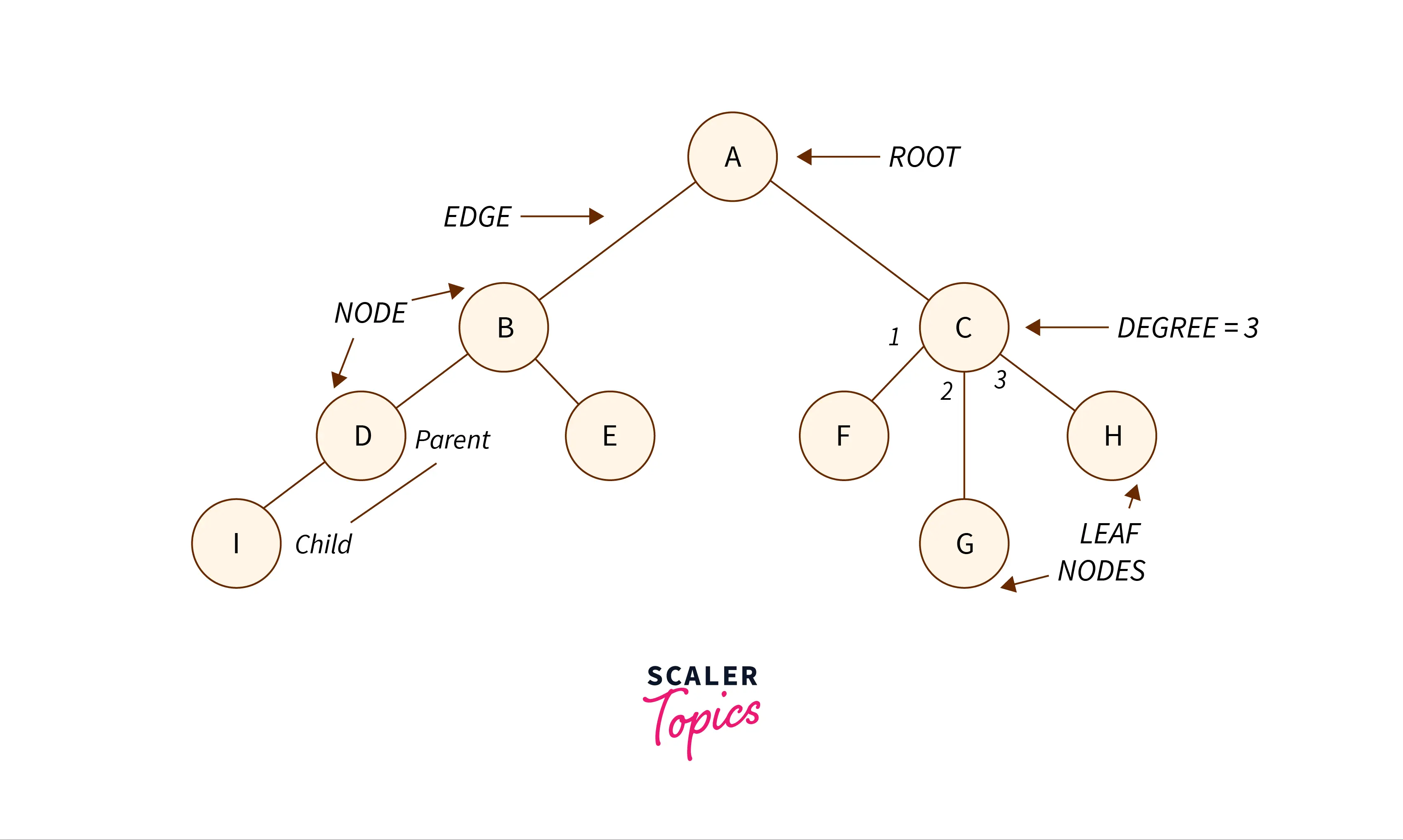
In this above image, you will be able to spot the nodes - A, B, C and so on. The root node is A, the leaf nodes are I, E, F, G, and H. The node D is a direct parent to node I and the node B is an indirect parent to node I. The child nodes of A are B and C. Degree of node C is 3 since you can connect 3 nodes to node C. The height of this tree is 3 since there are 3 levels after root node, and depth from node D is 2, depth from node G is 3.
General Tree
A general tree is a type of tree wherein there is no constraint placed on the hierarchy of the tree, i.e., every node can have an infinite number of children. The general tree is a super-set of every other tree type.
Binary Tree
A binary tree is a type of general tree, except, with a constraint - a node can have only two child nodes. The children nodes are known as the left child node and right child node.
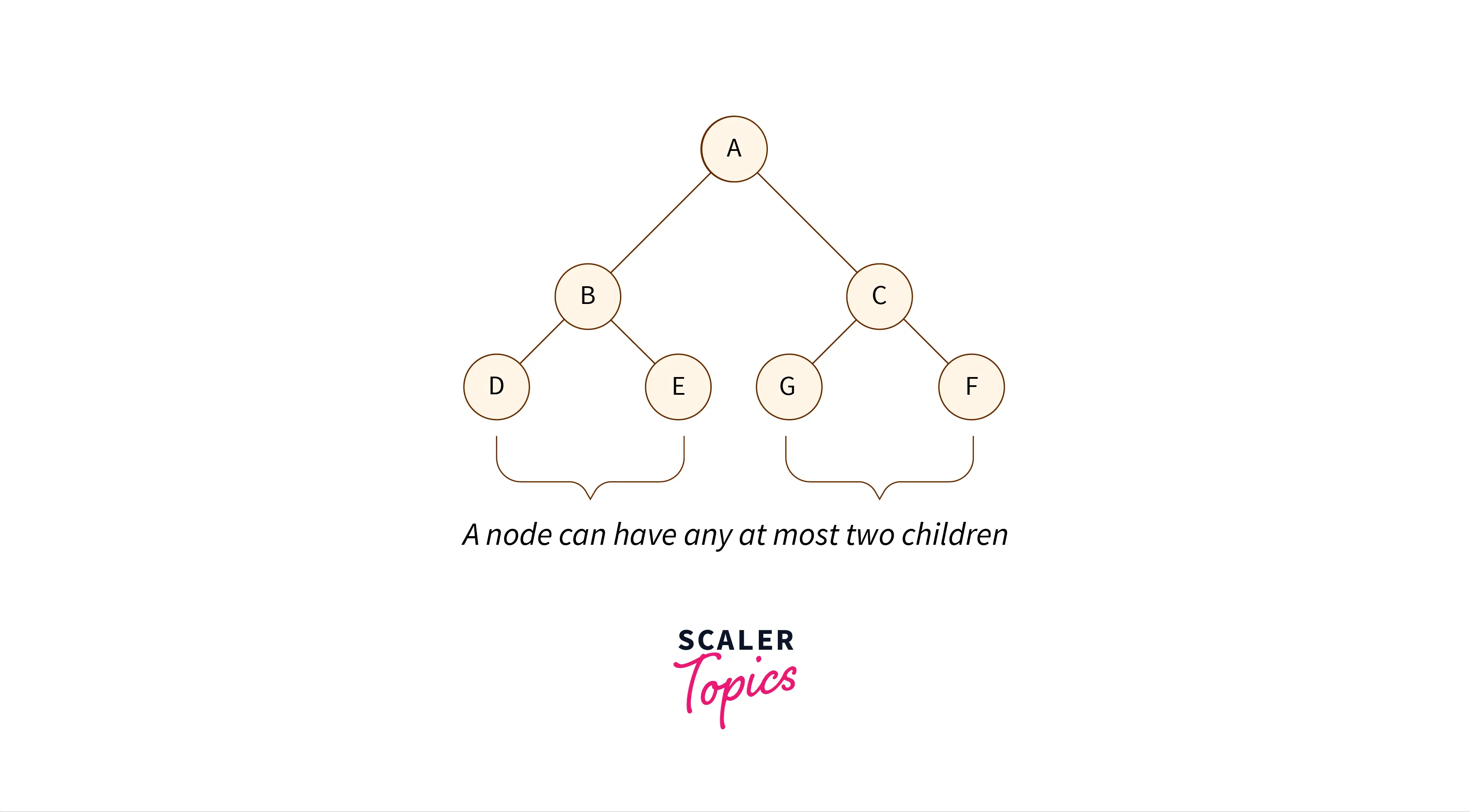
There are mainly 5 types of binary trees:
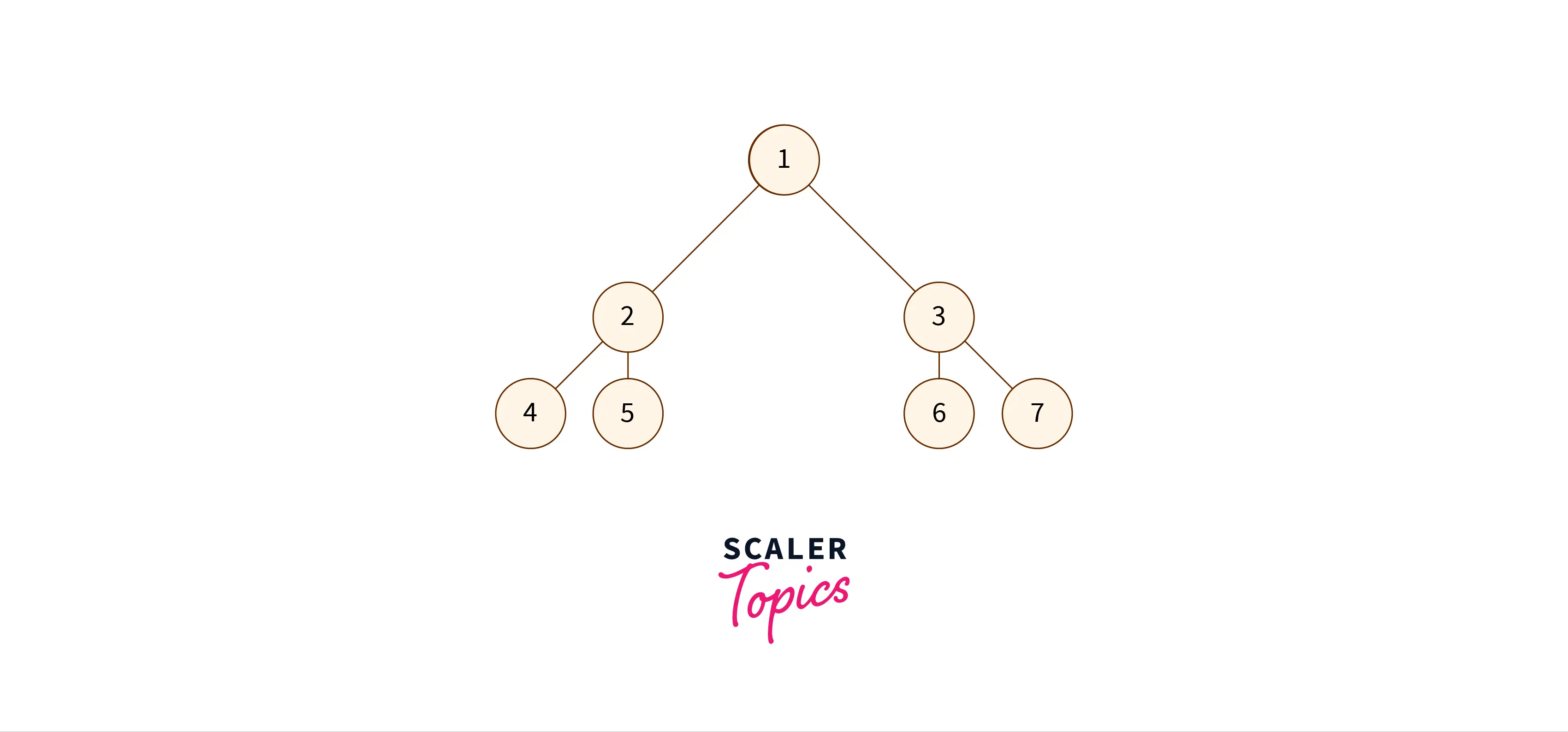
- Perfect binary tree: All the leaf nodes of this tree are at the same level. Every internal node of a perfect binary tree has 2 child nodes.
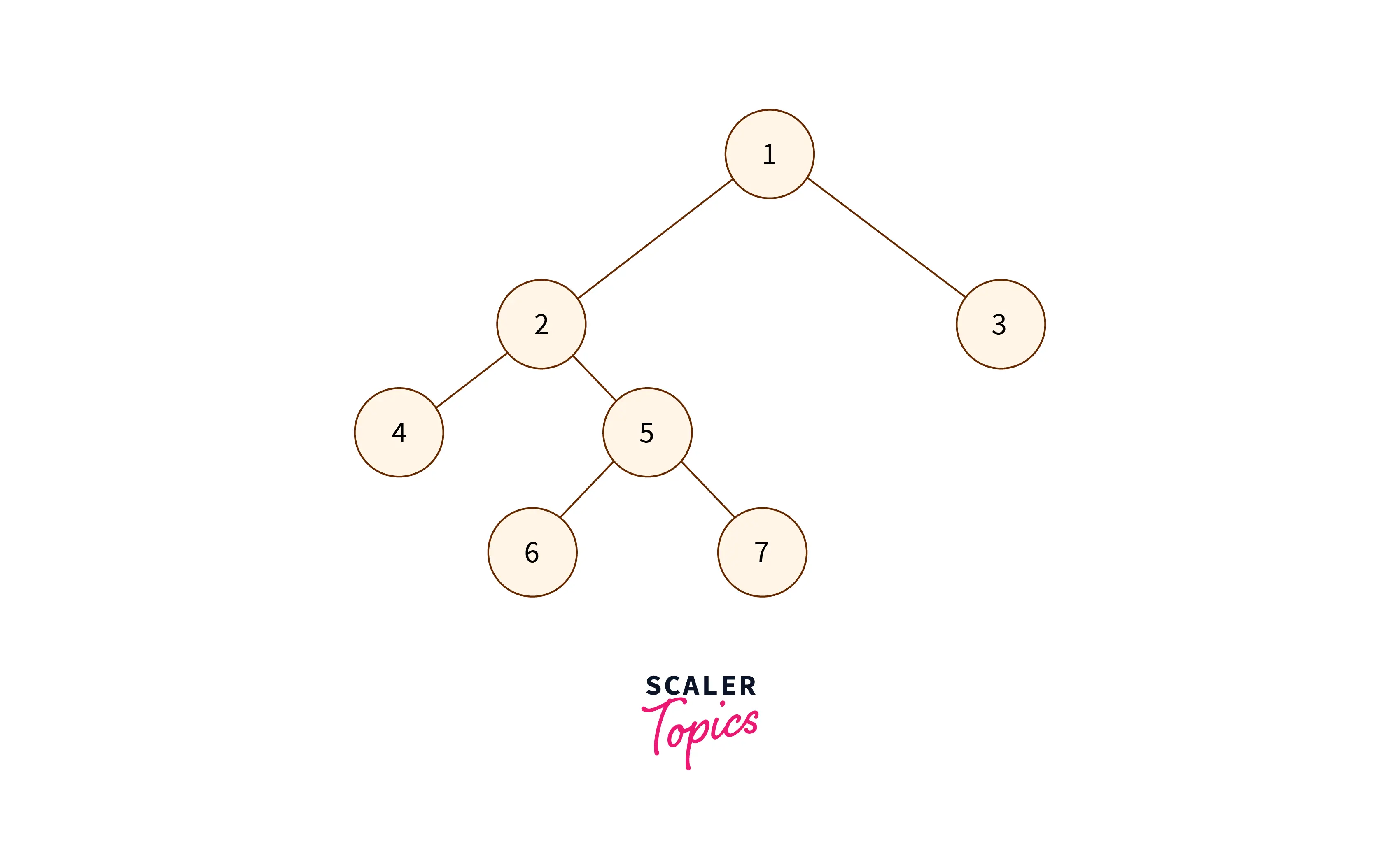
- Full binary tree: All the internal nodes of a full binary tree have two or no child nodes.
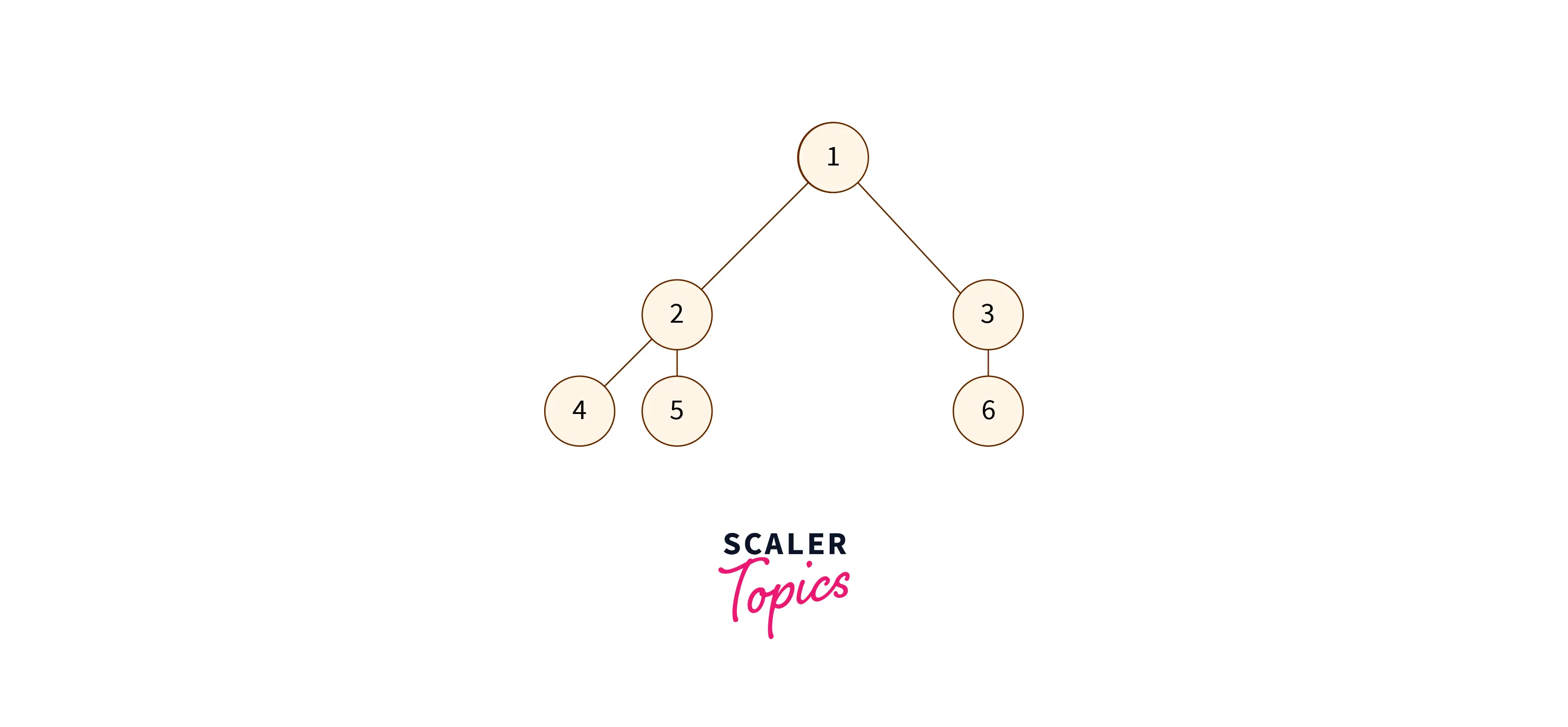
- Complete binary tree: Every level except the last one are full of nodes.
- Degenerate binary tree: Every internal node of the degenerate binary has just one child.
- Balanced binary tree: The height of the left and right subtree of any node differ by either 0 or 1.
The following are the important time complexities (worst case) of binary tree operations:
- Searching: O(n) Since we have to traverse all elements one by one. n = number of nodes
- Insertion: O(n) Again, for insertion, in the worst case we have to traverse all elements to find the right place to insert. n = number of nodes
- Deletion: O(n) Same as insertion. n = number of nodes.
Binary Search Tree
A binary search tree is similar to a binary tree, with certain restrictions. The value of the left child in a binary search tree is always smaller than that of the parent node, and the value of the right child is larger than that of the parent node in the binary search tree. This property makes the binary search tree optimal for search operations.
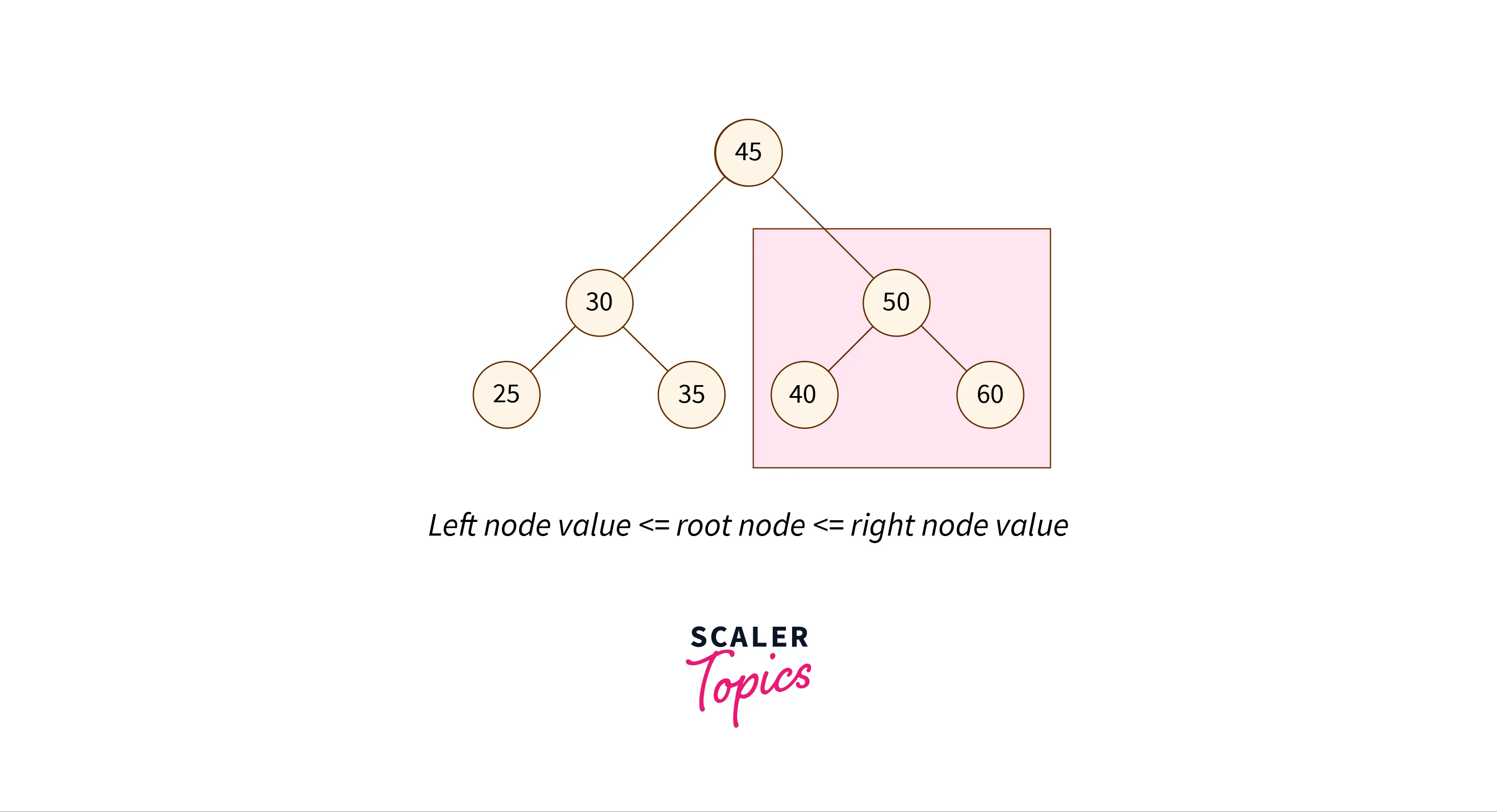
To learn more about the binary search tree in detail, refer to this article by scaler topics. The following are the important time complexities (worst case) of binary search tree operations:
- Searching: O(h) The general time complexity is O(h) where h is height of the BST, however worst case is still O(n).
- Insertion: O(h) Again, for insertion, in the worst case we have to traverse all elements to find the right place to insert, so the worst case time complexity is still O(n) but in general, the time complexity is O(h).
- Deletion: O(h) Same as insertion.
AVL Tree
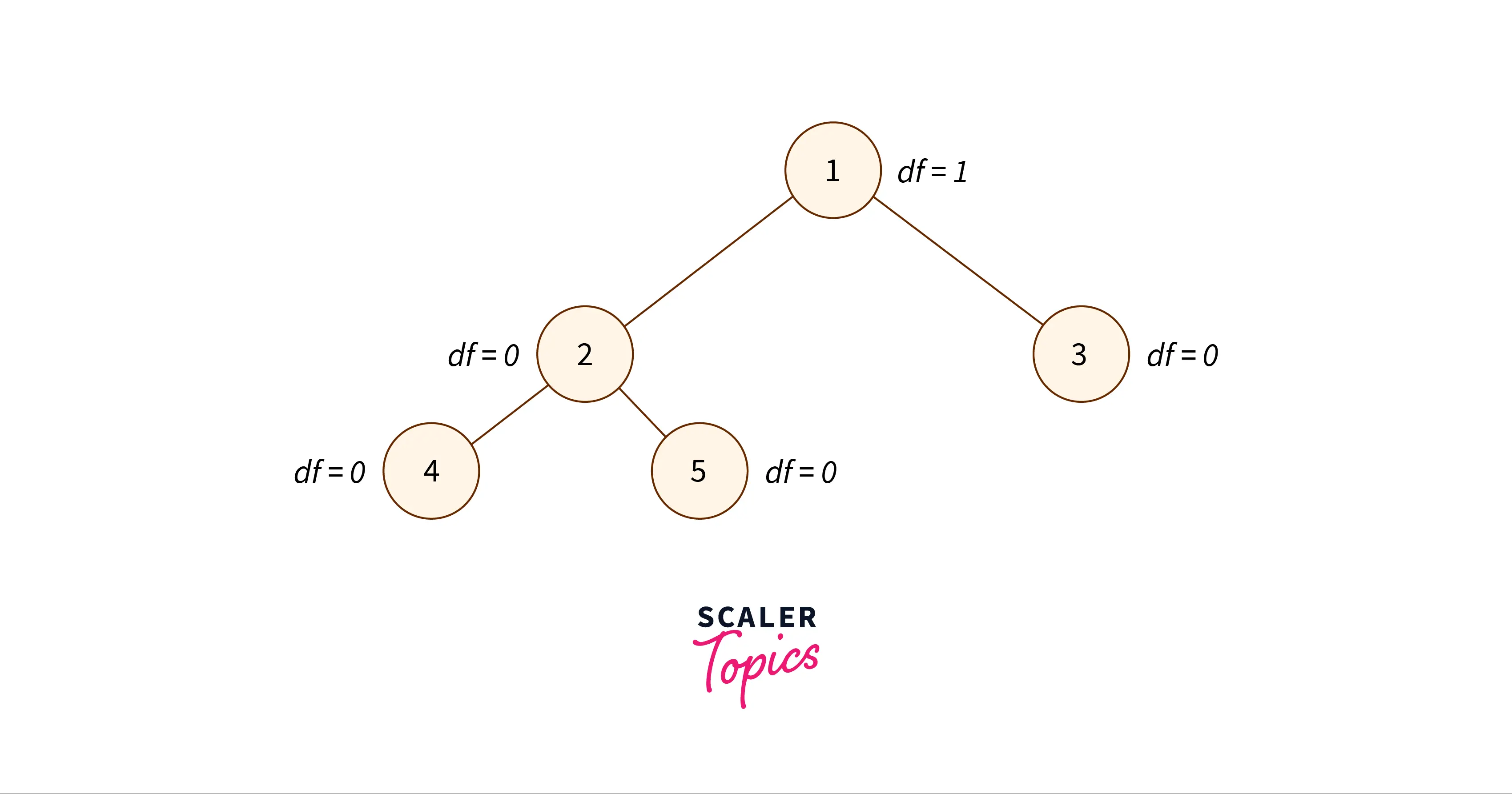
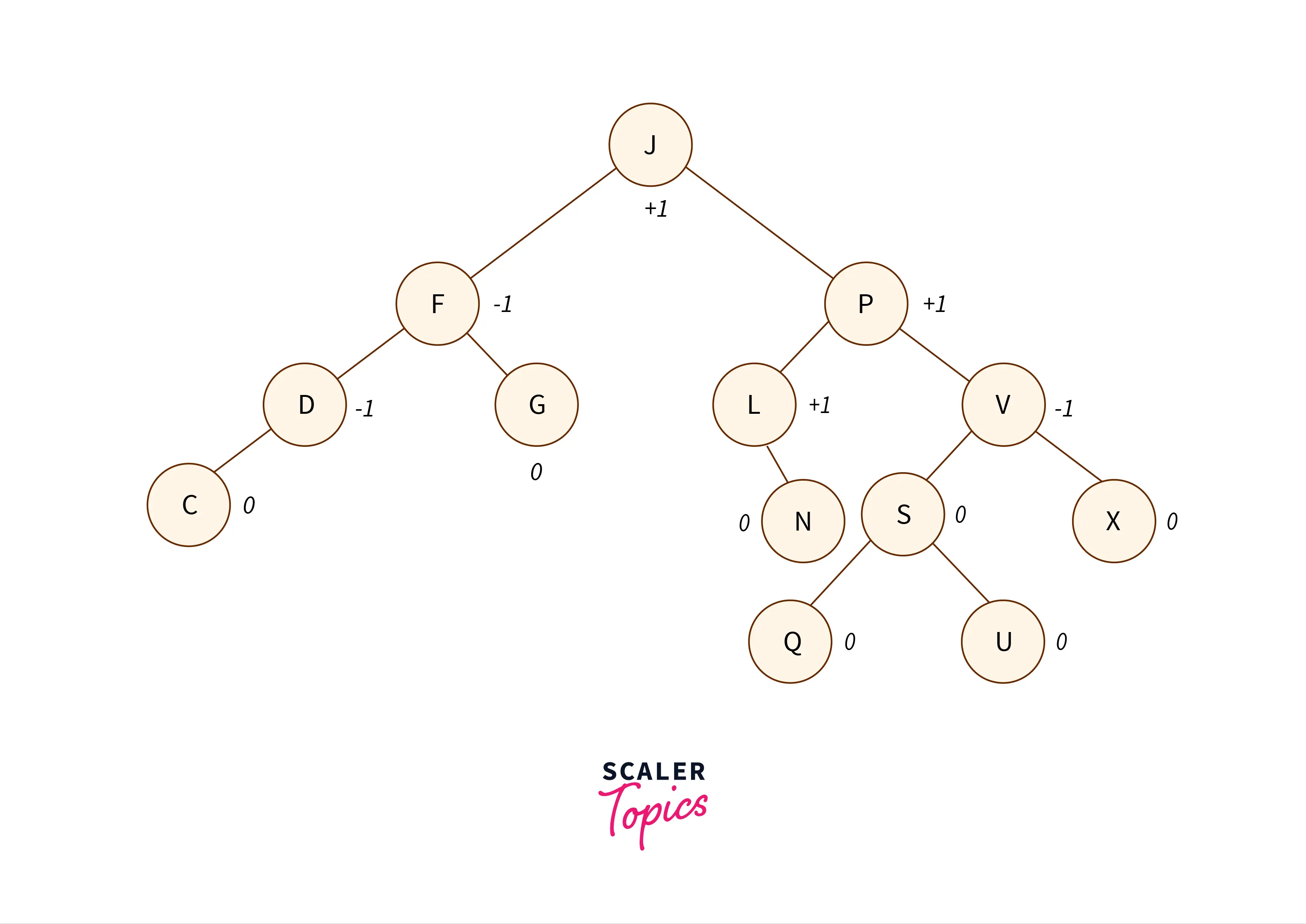
A self-balancing binary search tree is called an AVL tree. In an AVL tree, a balancing factor is given to every node in the tree which depends on whether the tree is balanced or not. These balancing factor values vary between -1, 0, and 1.
- If the right subtree is one level higher than the left subtree of a node, then the balancing factor value of that node is -1.
- If both, the left and right subtrees are at the same level, the balancing factor value is given as 0.
- If the left subtree is one level higher than the right subtree then the balancing factor is 1.
One subtree could be more than one level higher than the other subtree, in that case, the tree must be re-balanced using different rotation techniques to bring all balancing factor values between -1, 0, and 1.
To learn more about the AVL tree, refer to the scaler blog on AVL tree.
The following are the important time complexities (worst case) of AVL tree operations:
- Searching: O(log(n)) n = number of nodes.
- Insertion: O(log(n))
- Deletion: O(log(n))
Red-Black Tree
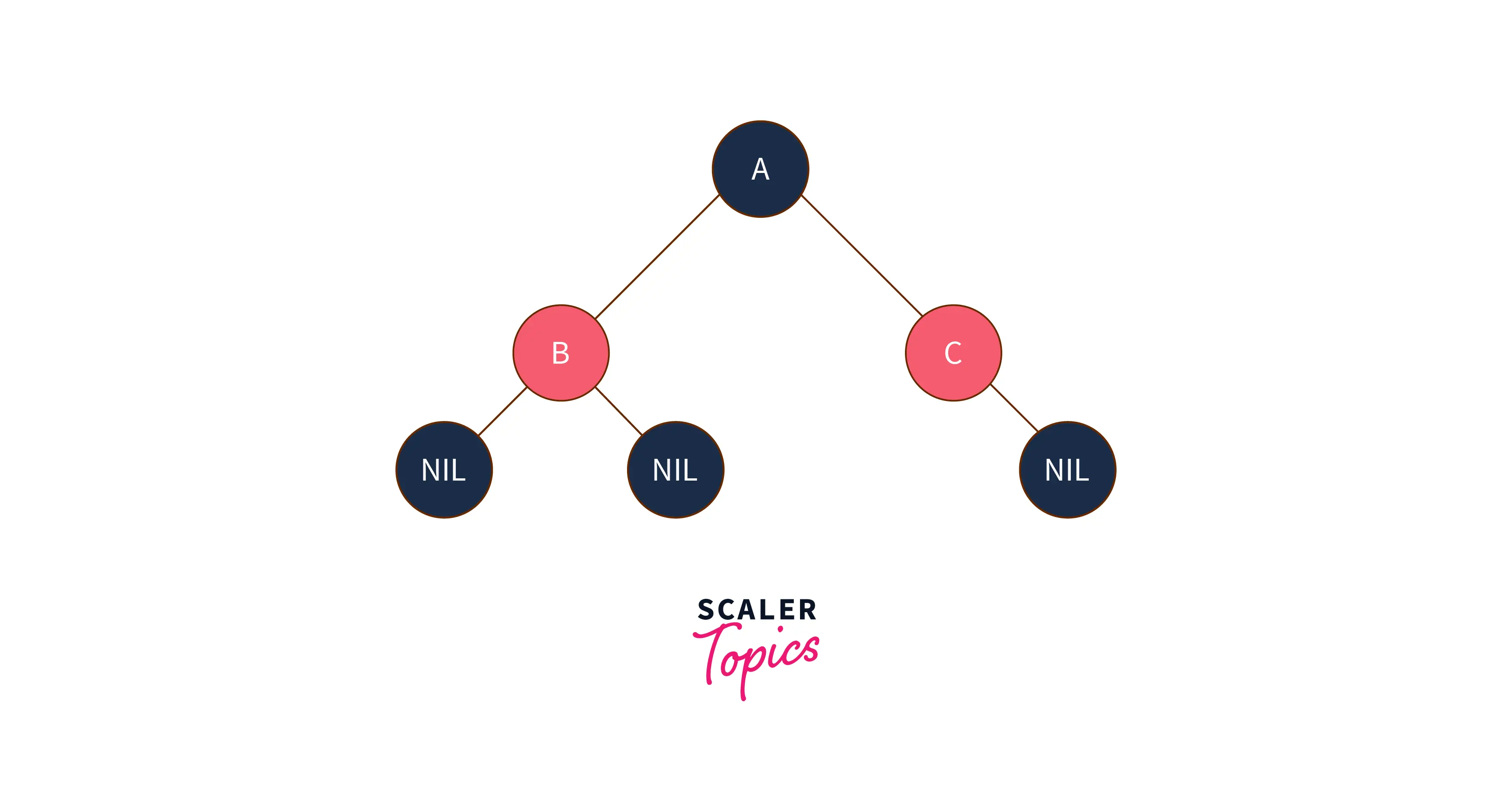
The red-black tree is also a self-balancing tree. Each node is either painted red or black. The rules of a red-black tree are:
- The leaf nodes and root nodes are black.
- If a parent node is red, both children nodes are black.
- There cannot be two adjacent red nodes.
- Every path from a node to the descendant NULL node (end of the path) must have an equal number of black nodes.
To learn about the red-black tree in detail, refer to this. The following are the important time complexities (worst case) of red-black tree operations:
- Searching: O(log(n))
- Insertion: O(log(n))
- Deletion: O(log(n))
N-ary Tree
It is a type of general tree, wherein every node can have only a maximum of 'n' children. A binary tree is a 2-ary tree i.e. having a maximum of 2 children per node.
A type of n-ary tree is a tree in which every node has either 0 or n child nodes.
Say for example if we have an n-ary tree with n = 4, the maximum number of child nodes that every node can have is four. No node can have more than 4 child nodes.
Splay Tree
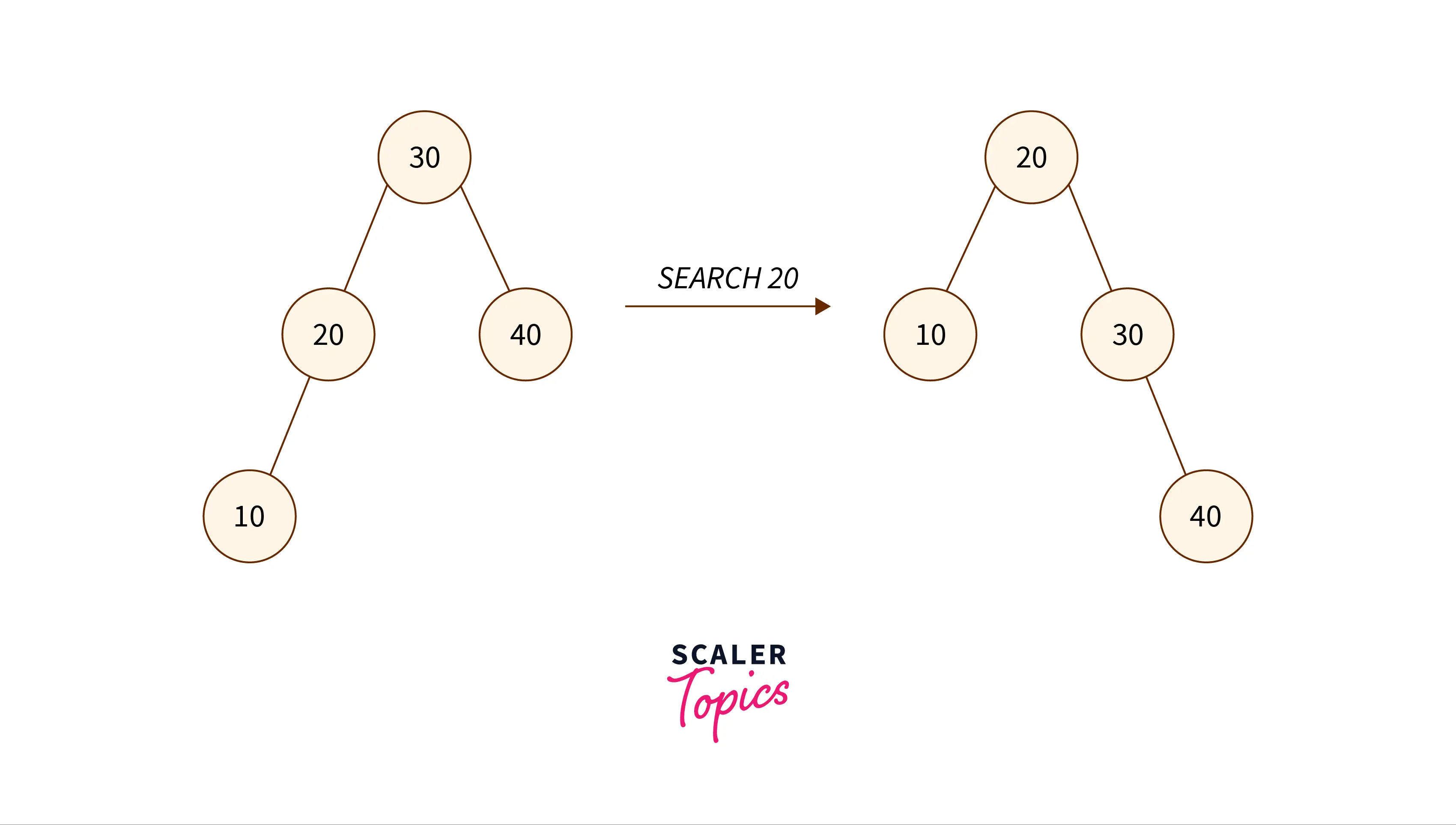
A Splay tree is another type of self-balancing tree that follows the properties of a binary tree. The advantage of a splay tree is that the elements that have been recently accessed are quicker to access if they are required to be accessed again. The splay tree performs a 'splaying' operation which makes this access faster - the tree is rearranged so that certain elements are placed at the root of the tree.
To learn about the splay tree in detail, and the splaying operation, refer to this article.
The following are the important time complexities (worst case) of splay tree operations:
- Searching: O(log(n)) Where, n is the number of entries in the splay tree.
- Insertion: O(log(n)) Where, n is the number of entries in the splay tree.
- Deletion: O(log(n)) Where, n is the number of entries in the splay tree.
Treap Tree
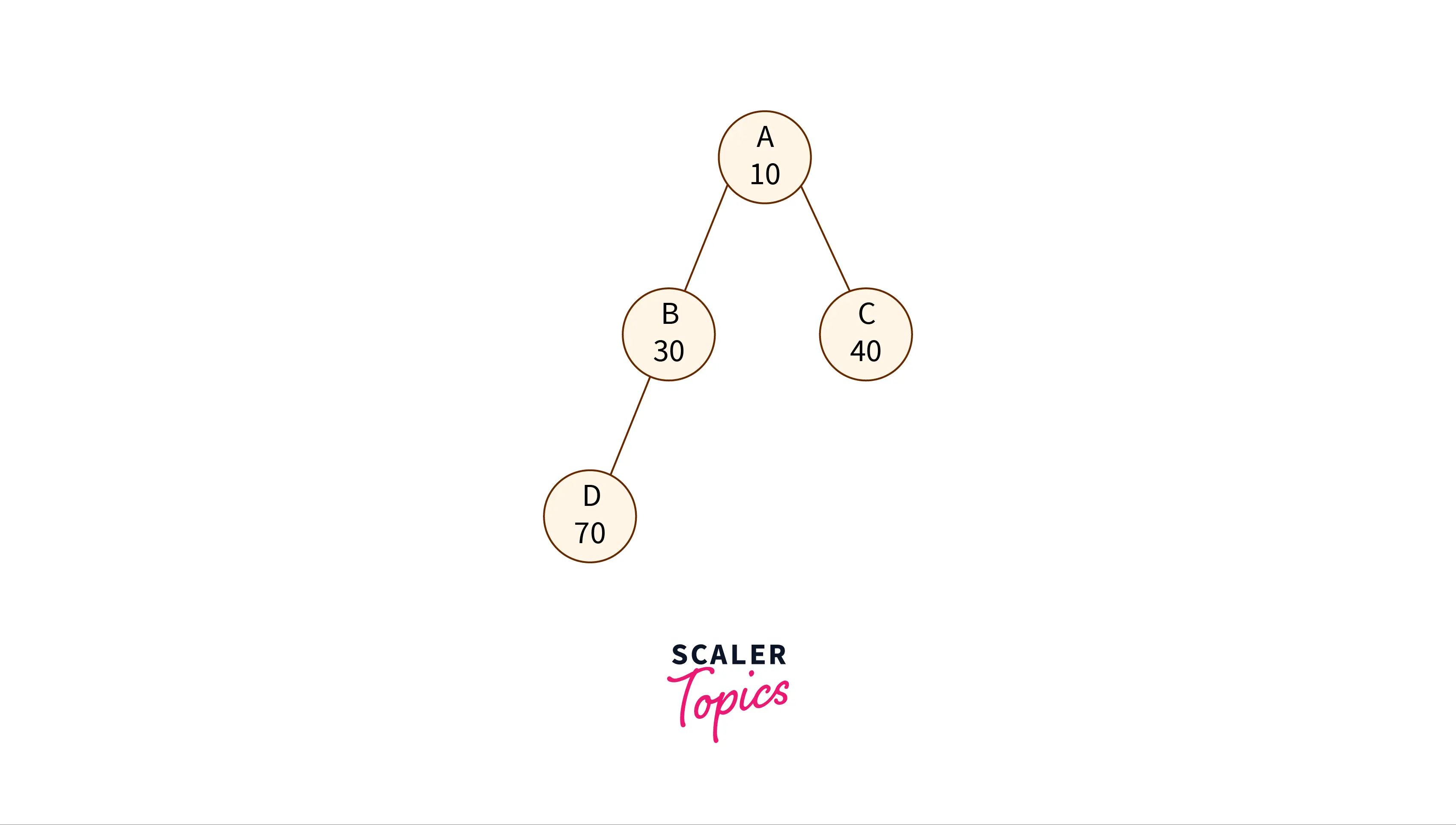
The treap tree is a mix of a binary search tree and a heap, hence the name treap, which means that the treap tree follows the properties of a binary search tree and a heap. In a treap tree, every node has two values - a key (its value) and a priority.
This key follows the BST property, i.e. the left child node will have a value that is lesser than the parent node, and the right child node will have a value higher than the parent node. The priority value of every node is assigned randomly, and it follows a max-heap property.
Here's what it looks like:
To read more about the treap tree, refer to this article by scaler topics. The following are the important time complexities (worst case) of treap tree operations:
- Searching: O(log(n)) Where, log(n) is height of the treap tree.
- Insertion: O(log(n)) Where, log(n) is height of the treap tree.
- Deletion: O(log(n)) Where, log(n) is height of the treap tree.
Segment Tree
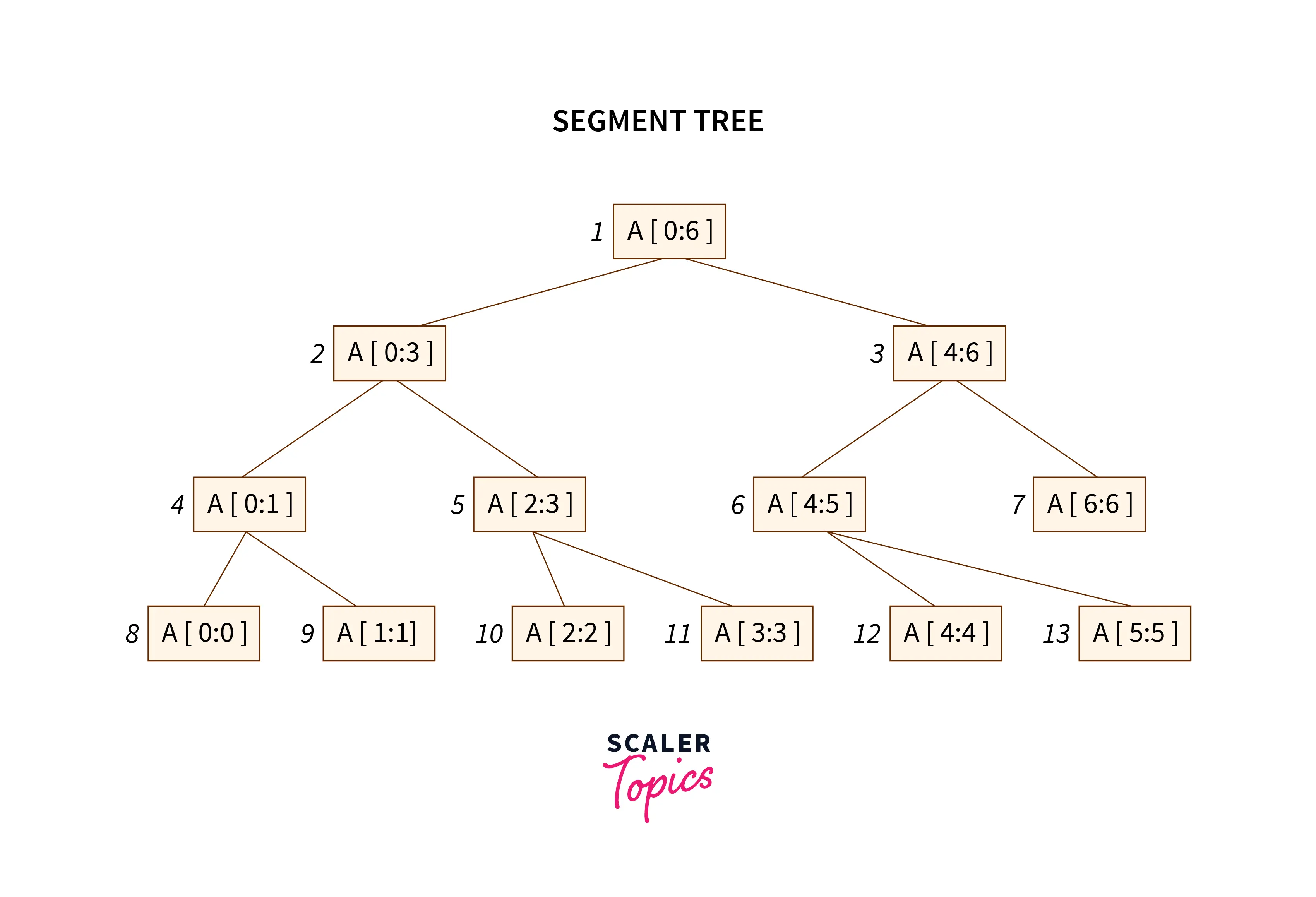
A segment tree is a binary tree that is used to store intervals or segments. Every node of the tree is used to represent an interval. A simple array can be used to represent a segment tree. This tree allows us to answer range queries over an array.
Let's say we have an array A of size N that represents a segment tree T.
- The root node of the tree will represent all elements of the array A[0
- 1] - Every leaf node of the tree will represent only one element of the array A[i] such that 0 <= i < N
- The internal nodes of the tree will represent the union of elementary intervals A[i : j] where 0 <= i < j < N.
Two operations can be done on a segment tree - update (update the value of a key) and query (given two indices, return the segment lying between the two indices).
The following are the important time complexities (worst case) of segment tree operations:
- Update: O(log2(n))
- Query: O(log2(n)) Where log2(n) corressponds to the number of levels in the segment tree.
The major use cases of segment trees are:
- Computational Geometry
- Machine Learning
- Geographic Information Systems (GIS)
- Square root decomposition which requires multiple queries done on segments in sqrt(n) time.
Trie
Trie is an advanced data structure and is also known as a prefix tree / digital tree that stores data in an efficient and ordered manner. Tries are generally used to store strings, as each node of a trie can hold up to 26 pointers.
Every node in a trie has two segments:
- A character
- A boolean value that is used to check if this character of the node represents the end of the word.
An example:
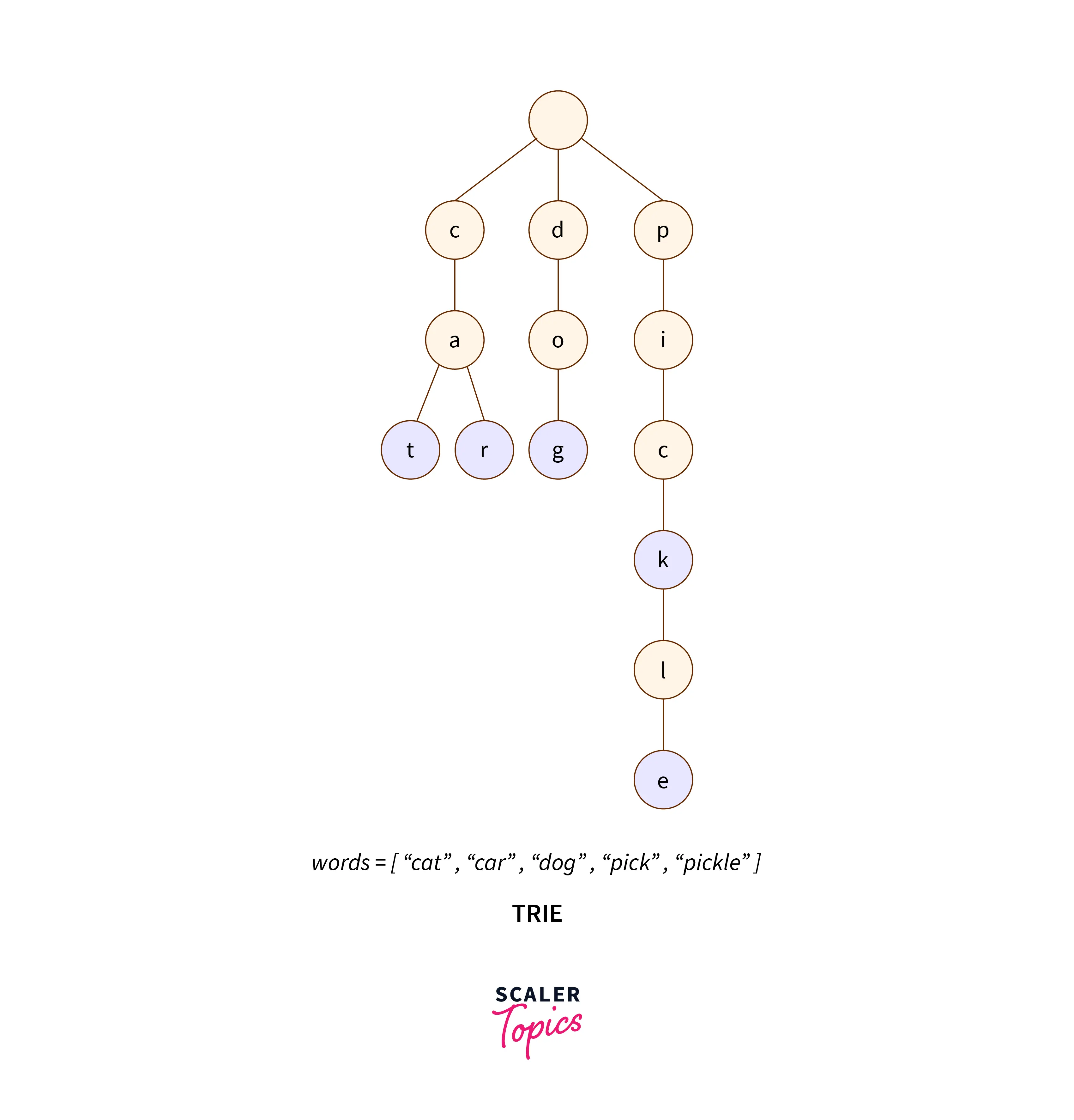
The following are the important time complexities (worst case) of trie operations:
- Creation: O(m*n) m = number of words in the trie n = average length of each word.
- Insertion: O(n) n = length of word.
- Searching: O(n) n = length of word.
Conclusion
- The tree data structure is non-linear. It comprises entities known as “nodes” and “edges”.
- Some important terminologies related to trees are - node, edge, root, parent, child, leaf node, subtree, degree, depth, level, and height.
- Types of trees:
- General tree: Every node can have an infinite number of children.
- Binary tree: Every node can have just two children. There are 5 types of binary trees -- perfect, full, complete, degenerate, and, balanced.
- Binary Search tree: Every left child has a smaller value than the parent and the right child has a value larger than the parent.
- AVL tree: Self-balancing tree that has balancing factor -> 1, 0, -1.
- Red-Black tree: Self-balancing tree that has red and black nodes.
- N-ary tree: Every node can have a maximum of 'n' children.
- Splay tree: Self-balancing tree that uses splaying operation for faster access of recently accessed elements.
- Treap tree: A tree that has the properties of both binary search tree and max-heap.
- Segment tree: A binary tree that stores segments or intervals. This tree is represented as an array.
- Trie: Also known as prefix tree, stores data in an efficient and ordered manner.
