Depth First Search (DFS) in Python
Learn via video course

Overview
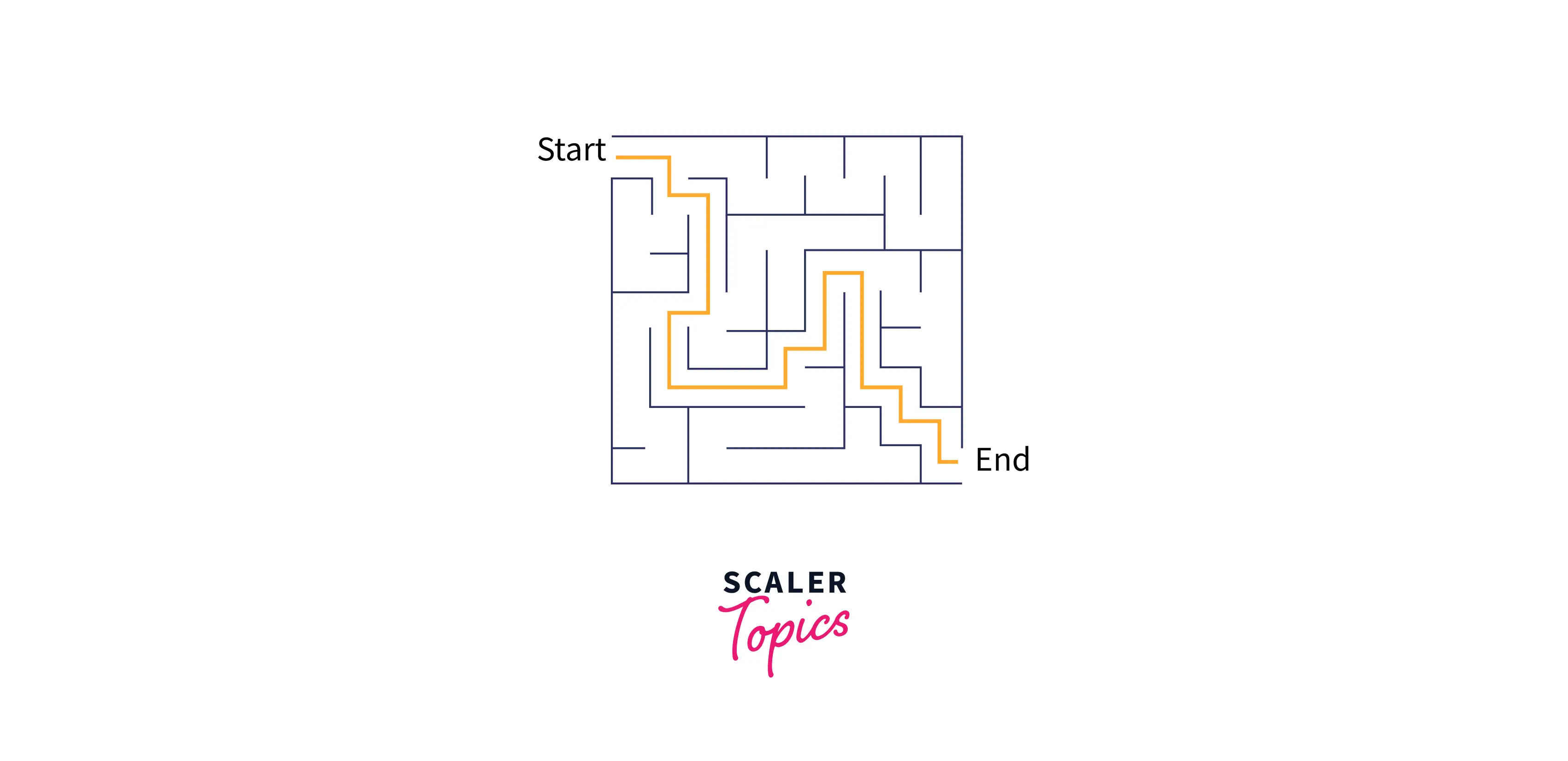
We can visit each node in a graph by iterating over all of its nodes and applying the algorithm to each node that has yet to be visited. Two algorithms are often used for graph traversal. These algorithms are depth-first search (DFS) and breadth-first search (BFS), although we will just discuss DFS here. DFS is diving deep into the graph and backtracking when it hits bottom. DFS is like solving a MAZE. We'll continue to walk through the path of the maze until we reach a dead end.
Scope
In this article on the topic of DFS Python, we will talk about the following things as shown below:
- What is depth-first search and how does it work with its algorithm?
- Implementation of depth-first search in Python and its complexity.
- And finally, we will look at the applications of depth-first search.
What is Depth First Search in Python?
In DFS, we continue to traverse downwards through linked nodes until we reach the end, then retrace our steps to check which connected nodes we haven't visited and repeat the process. In a depth-first search, we dive deep into the graph and then backtrack when we reach the bottom.
As we discussed above, the DFS is like solving a maze. We have to continue to walk along the path until we reach the end.
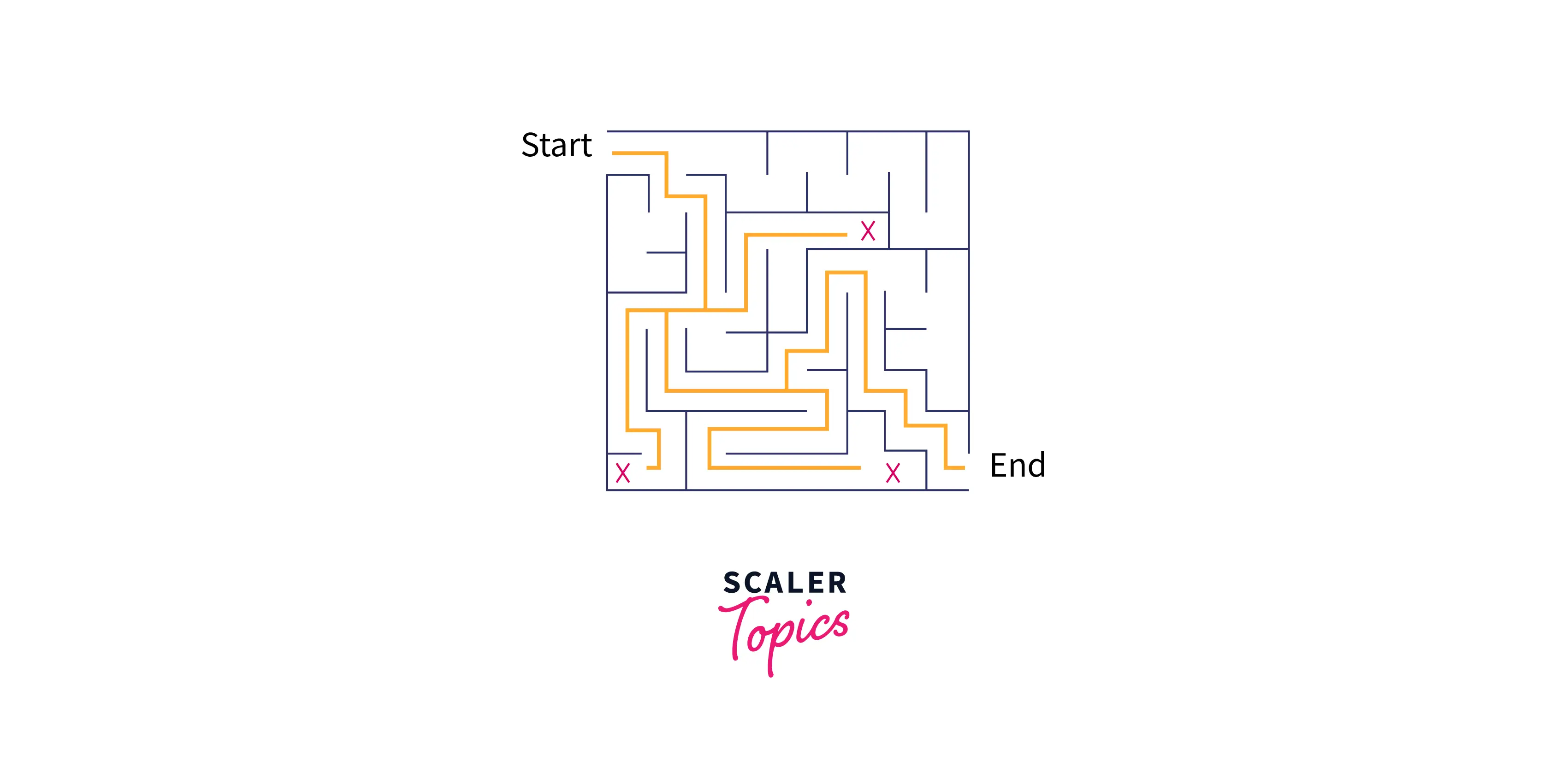
In the above image, as you can see, we are trying to get out of the image. So we are going deep into the maze, finding the various paths. When we reach the end, we backtrack until we find another path that we haven't walked yet, and repeat the process.
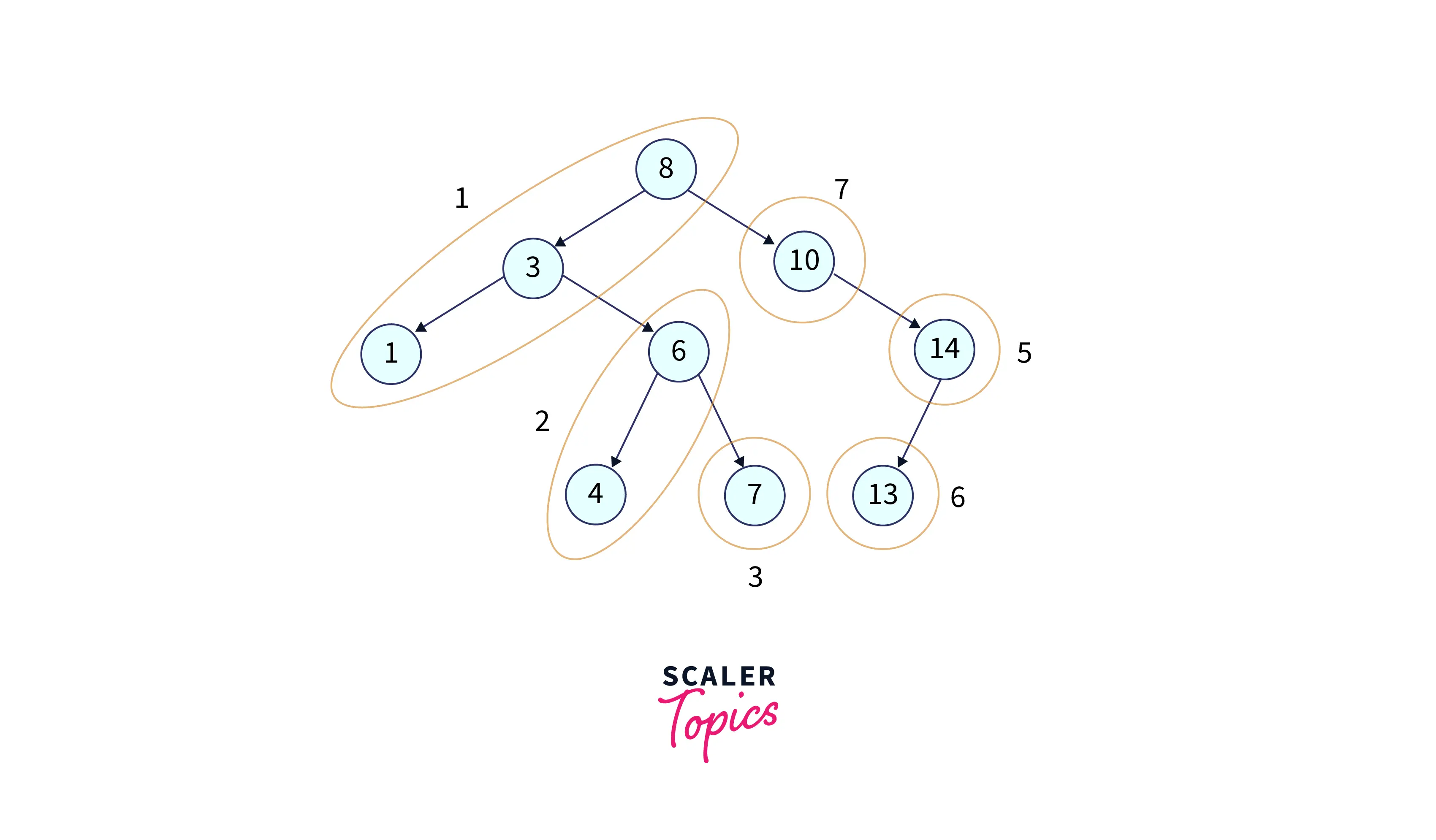
Let's have a look at the below example. We start with node 8, then go down to 3, then down to 1, and now we have hit the bottom, so start backtracking. Now at 3, we have one unvisited node, so go to 6, go down to 4, now hit the bottom, so backtrack again and reach node 6. Now we have one more unvisited node, i.e., 7, so go down to 7, now hit the bottom, so directly backtrack to node 8, now repeat the process.
The depth-first algorithm chooses one path and continues it until it reaches the end.
Algorithm of DFS in Python
To implement DFS, we use the Stack data structure to keep track of the visited nodes. We begin with the root as the first element in the stack, then pop from it and add all the related nodes of the popped node to the stack. We repeated the process until the stack became empty.
Every time we reach a new node, we will take the following steps:
- We add the node to the top of the stack.
- Marked it as visited.
- We check if this node has any adjacent nodes:
- If it has adjacent nodes, then we ensure that they have not been visited already, and then visited it.
- We removed it from the stack if it had no adjacent nodes.
With every node added to the stack, we repeat the above steps or recursively visit each node until we reach the dead end.
Implementation of DFS in Python
Introduction
Consider the following graph:
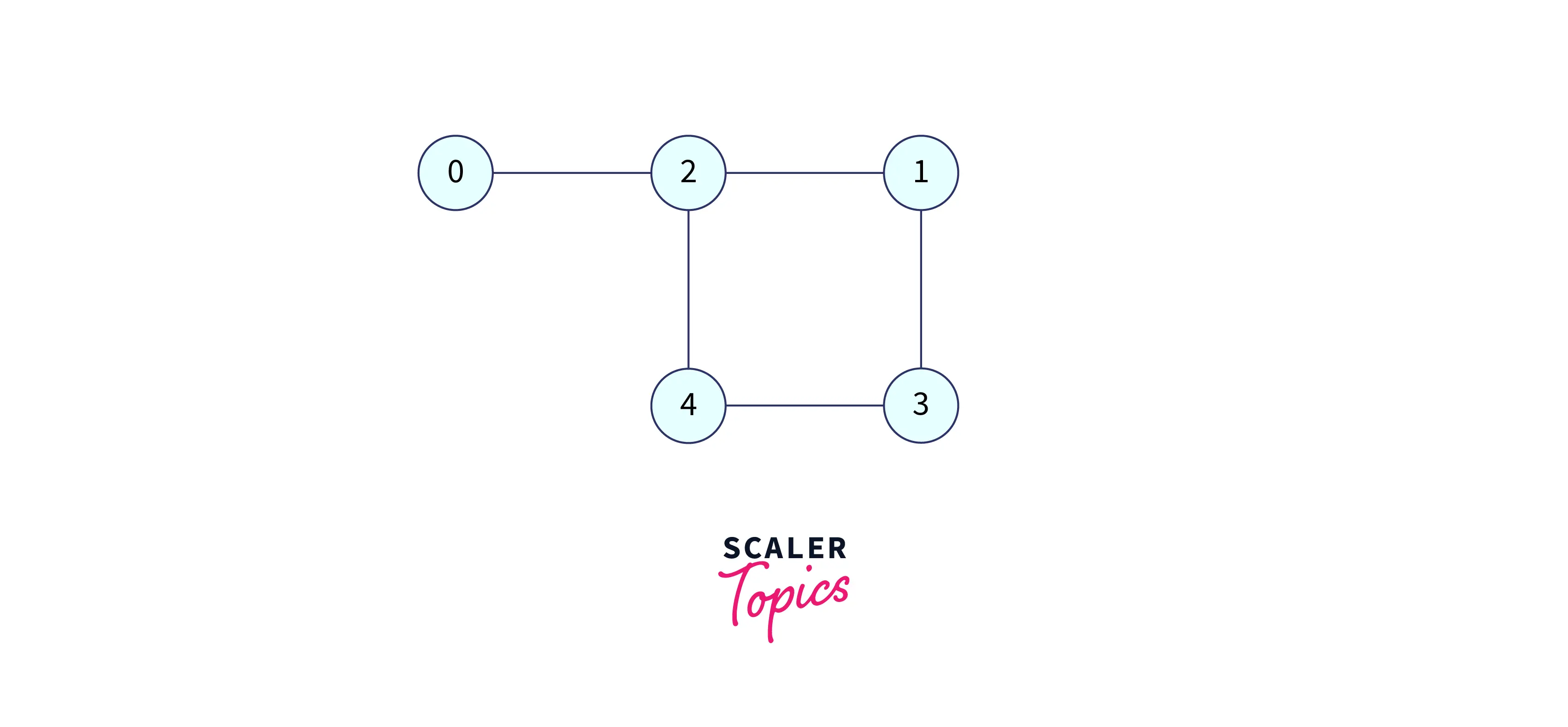
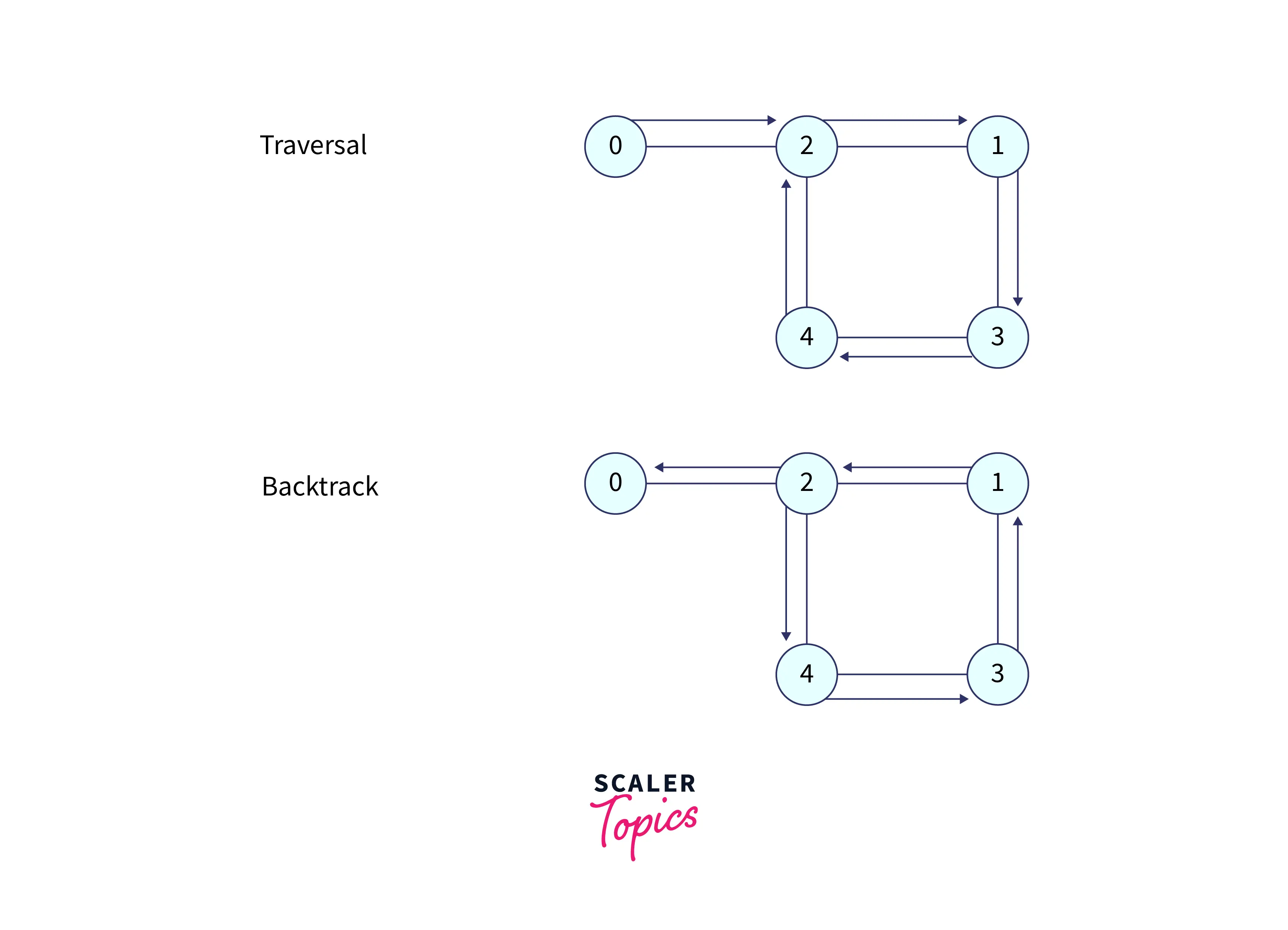
Let’s take one case of traversal, like how our DFS algorithm could traverse this graph. It could start from 0 to 2 to 1 to 3 to 4 to 2, but 2 is visited and 4 also doesn’t have any adjacent nodes that are not visited, so it starts backtracking from 4 to 3 to 1 to 2 to 0.
See the traversal given below.
Let's have a look at the adjacency list of the above graph:
Now, we will look at how this adjacency list works during DFS traversal:
We start from node 0. It has one adjacent node only, i.e., 2, so visit 2.
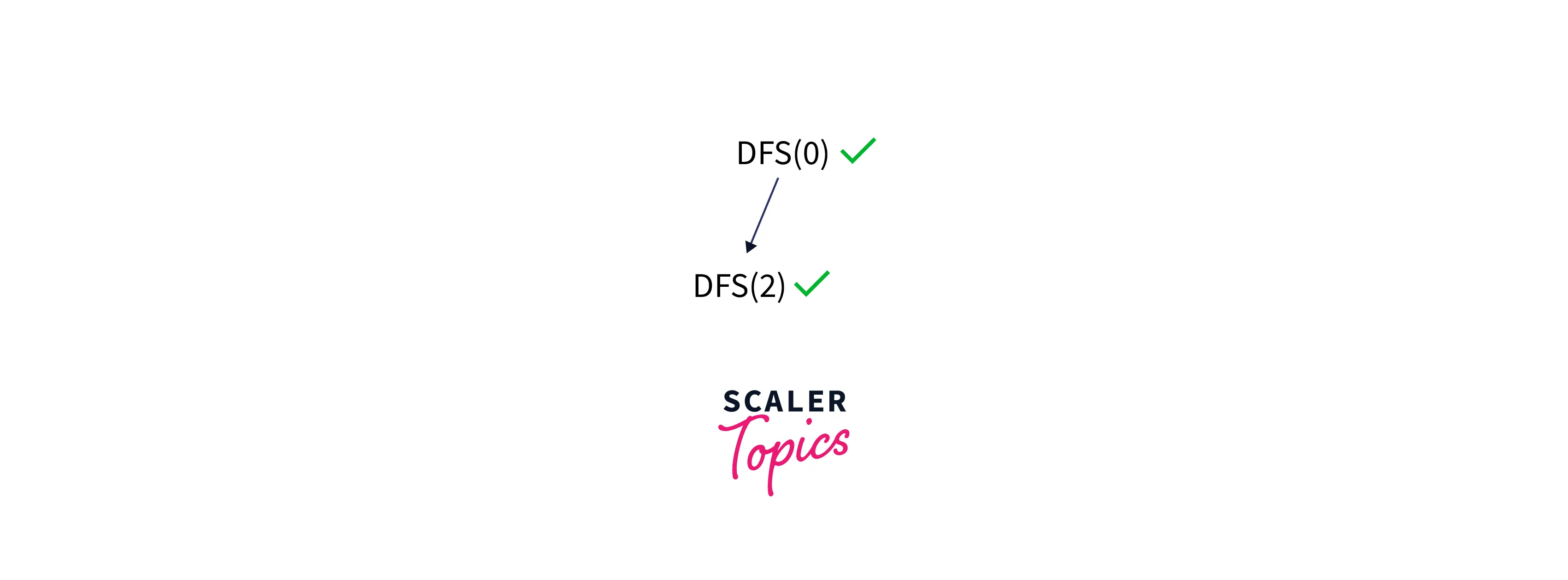
Node 2 has three adjacent nodes: 1, 0, and 4. But 0 has already been visited, so now we will choose to visit 1, so visit 1.
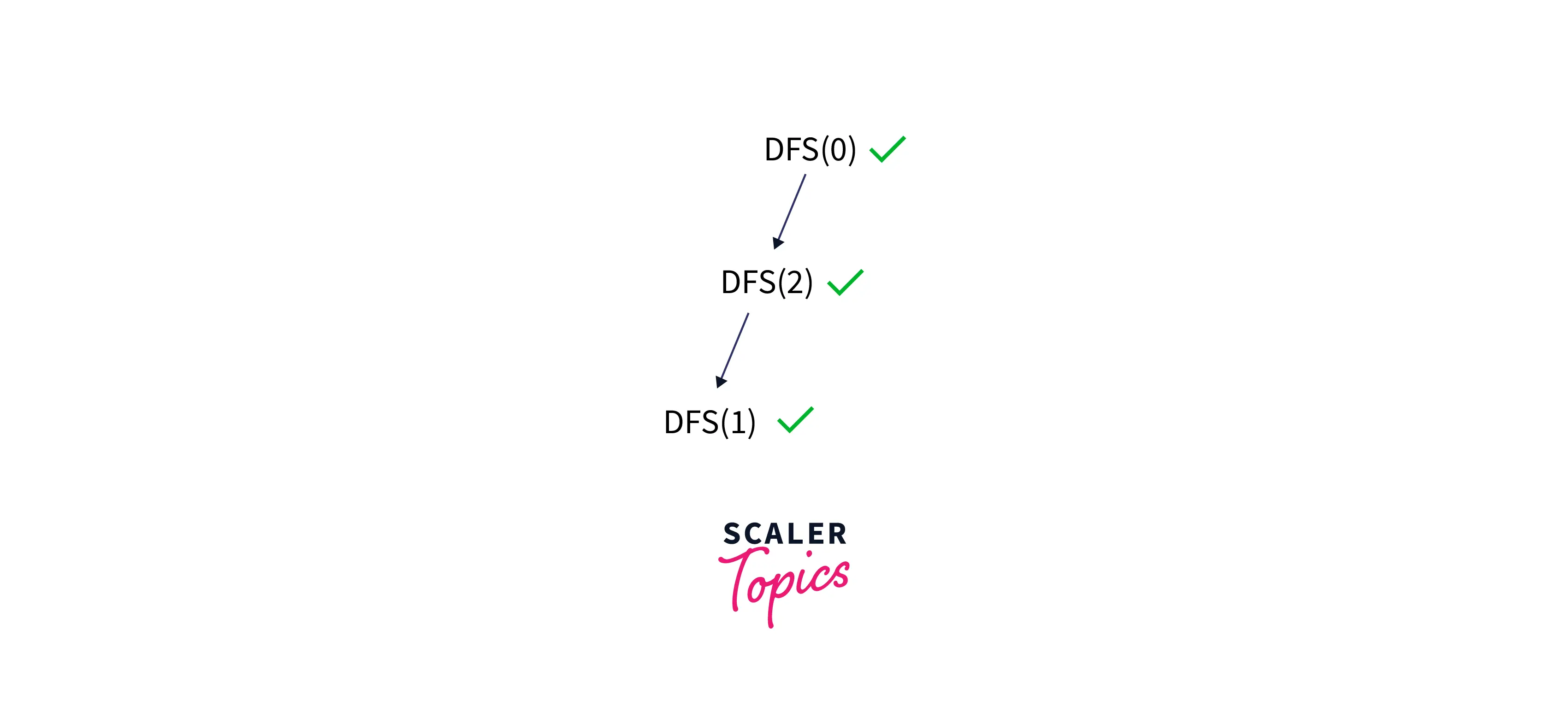
1 has two adjacent nodes, i.e., 2 and 3. But 2 have already visited, so we'll choose adjacent node 3 and visit 3.
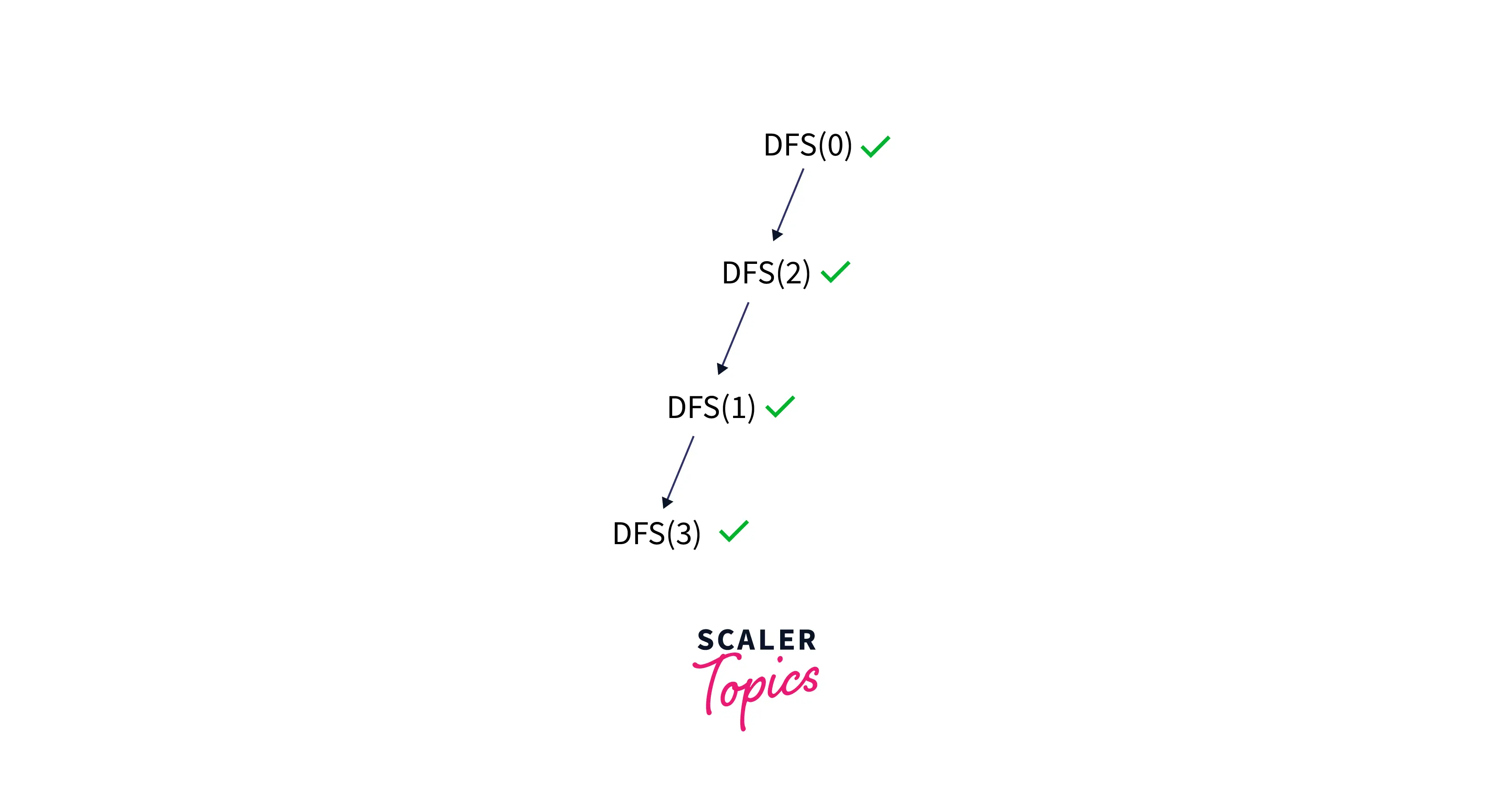
Now we are at node 3, and node 3 has two adjacent nodes, i.e., 1 and 4, but 1 has already visited, so we will now visit 4.
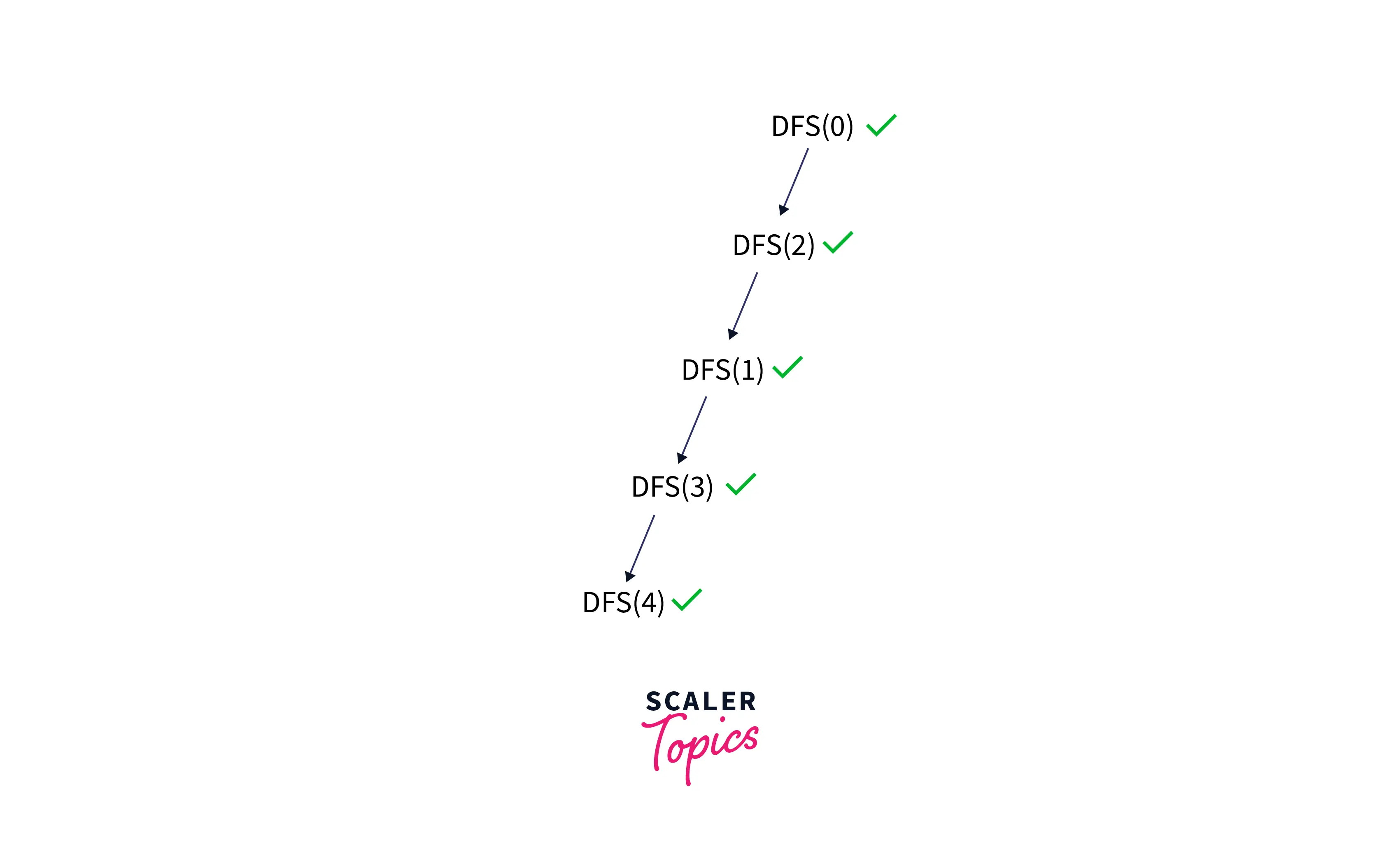
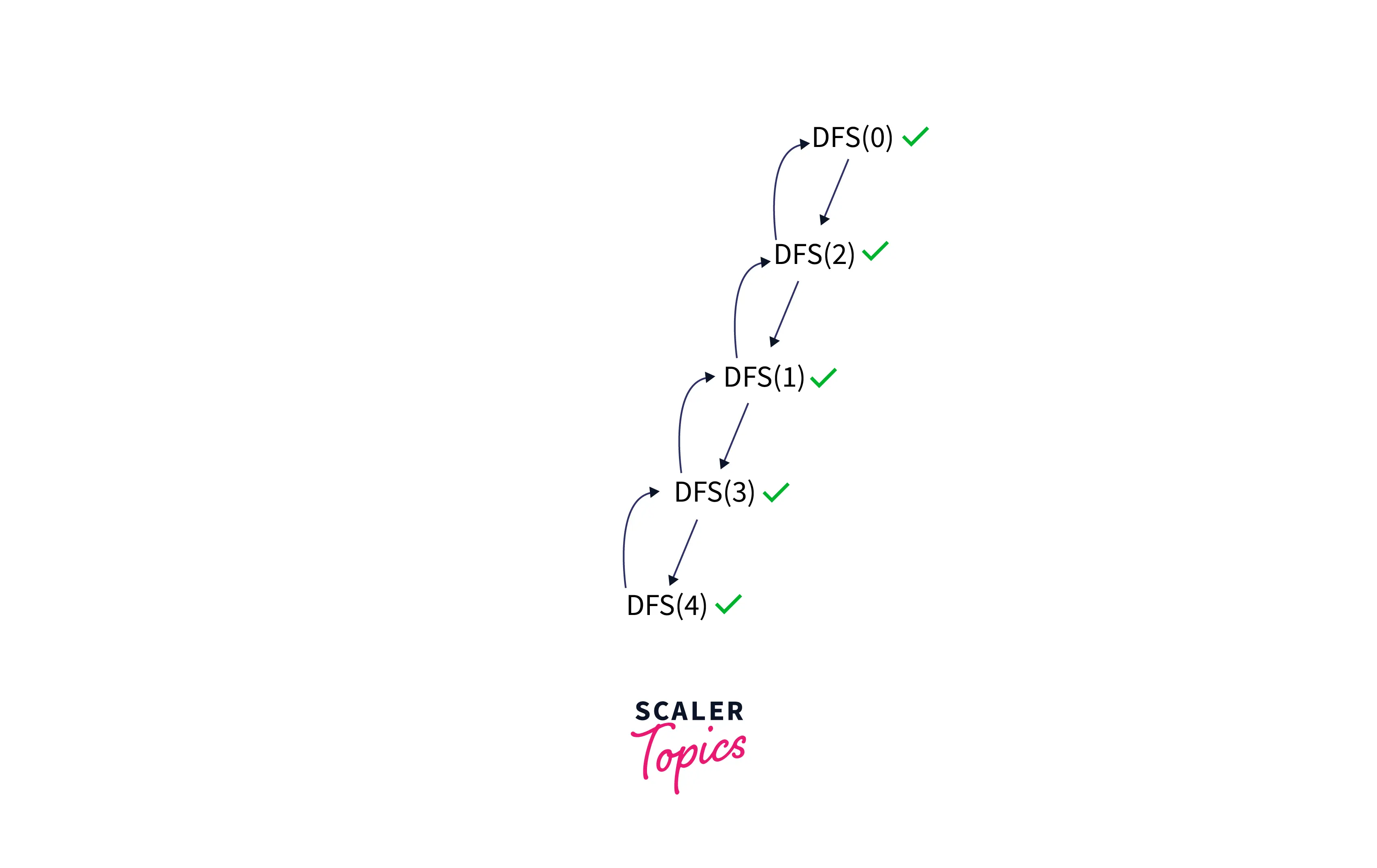
Attention, here now we are at node 4, and node 4 has two adjacent nodes, i.e., 2 and 3, but both are visited, so we have only one option remaining, and that option is to go back, which means to backtrack. So we will start backtracking from 4 to 3 to 1 to 2 to 0, and here the traversal ends. Finally, when we backtrack, we must check for each node to see if we have visited all of its adjacent nodes, and if not, we must explore all of them. Below is the figure to show the backtracking.
Code
Output:
Explanation
We created a graph with five nodes in the above code. Our source node is 0. We have a visited array that stores all the nodes that have been visited and a component array that stores the answer. Then we call the dfs function, passing it to the source node, visited array, component array, and graph. When we call the dfs function with any node, we first visit that node and add it to the answer array. Then we visit all of the adjacent node nodes of the given node.
Time Complexity of DFS implementation in Python
Time Complexity
On a directed graph, the average time complexity of DFS is O(V+|E|), where V is the number of vertices and E is the number of edges; on an undirected graph, the time complexity is O(V+2|E|)(each edge is visited twice).
The average time complexity of DFS on a tree is O(V), where V is the number of nodes.
Space Complexity
The space complexity of the DFS algorithm is O(V), where V is the number of vertices.
Examples of DFS in Python
Example 1
We have taken an undirected graph with 5 vertices.
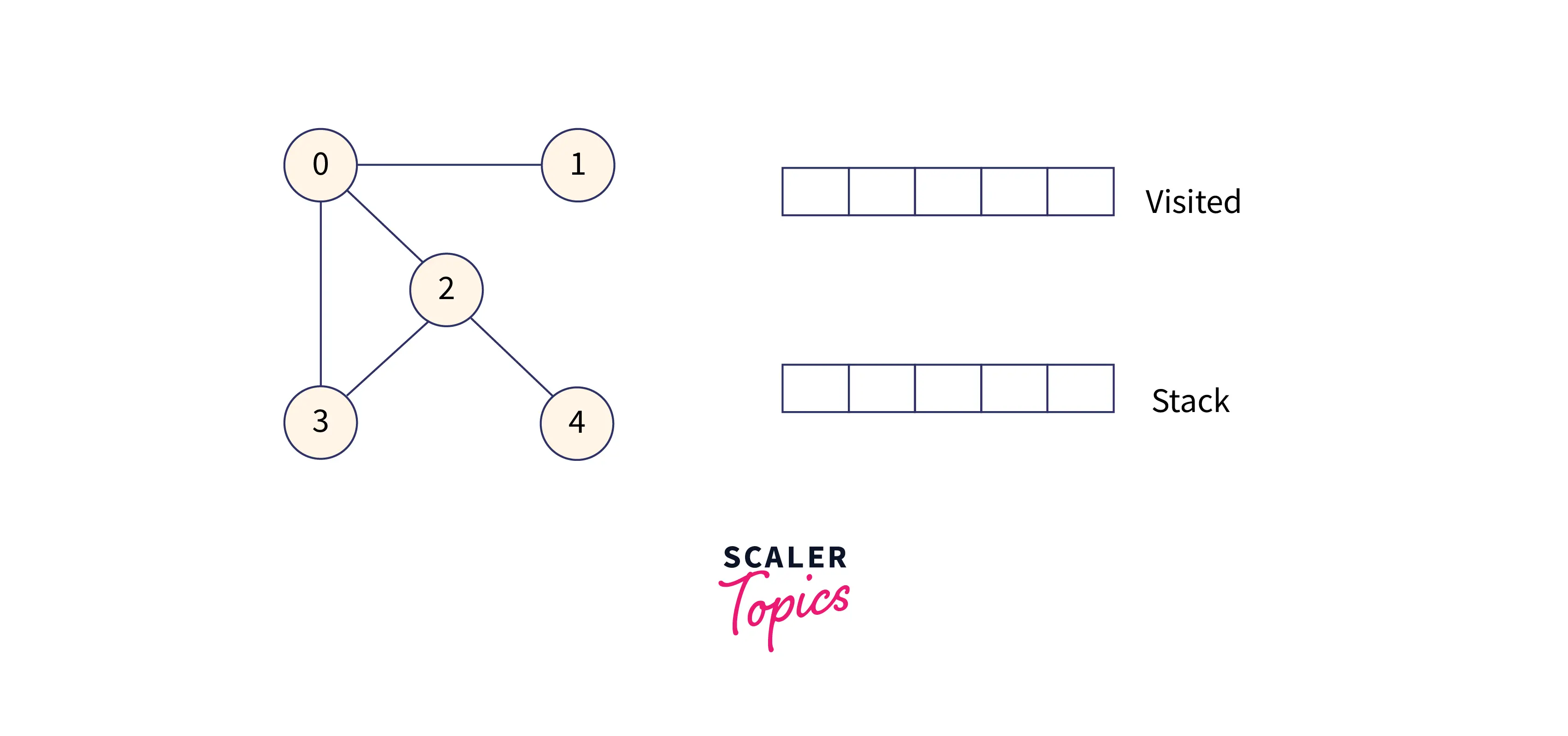
Below is the adjacency list of the above graph:
Visit 0 and put it in the visited list. 0 has three adjacent nodes: 1, 2, and 3. So put them in a stack for the next search.
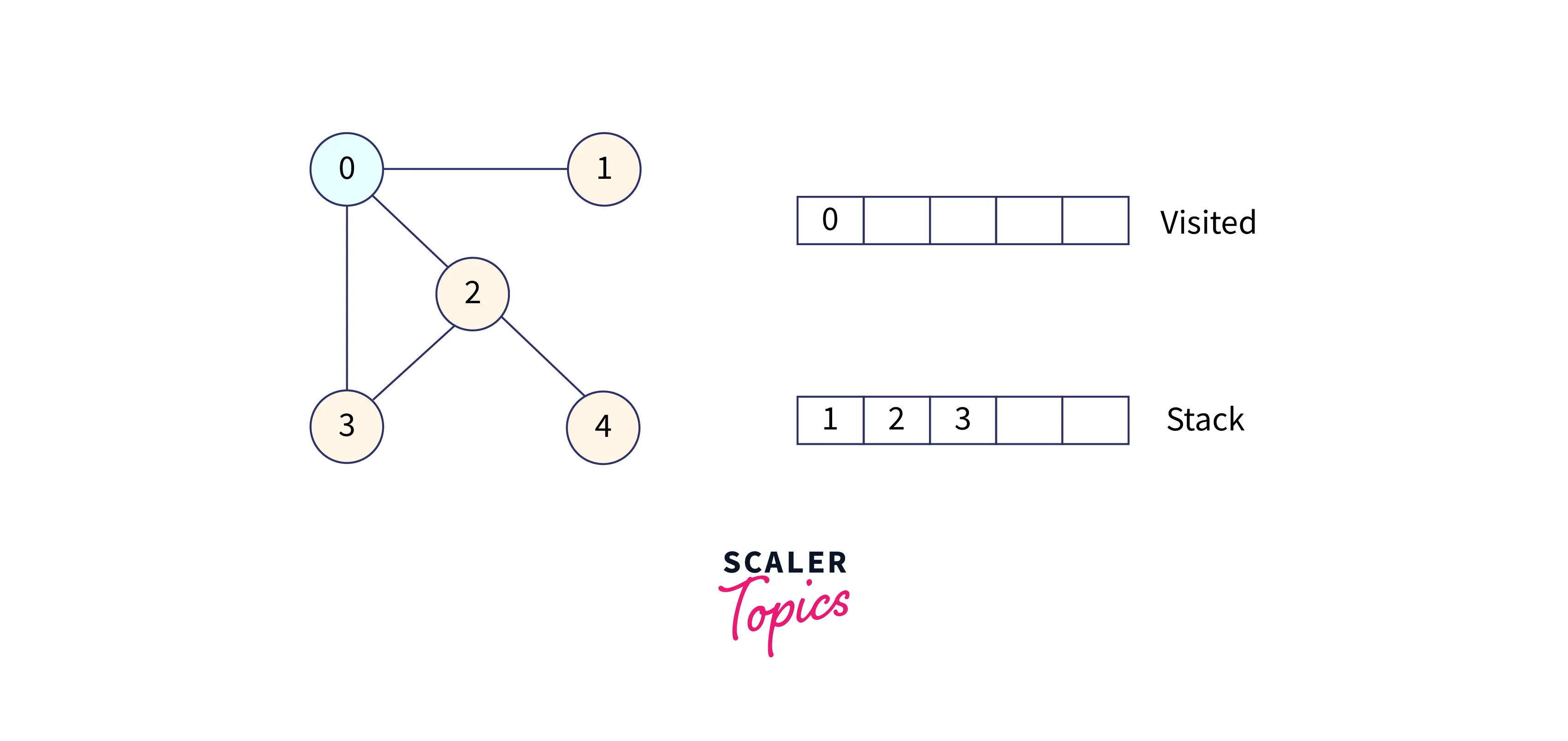
Now, we will visit the element at the top of the stack, i.e., 1, so visit this node and put its adjacent nodes into the stack, since it has only one adjacent node, i.e., 0, and it is already visited, so move forward.
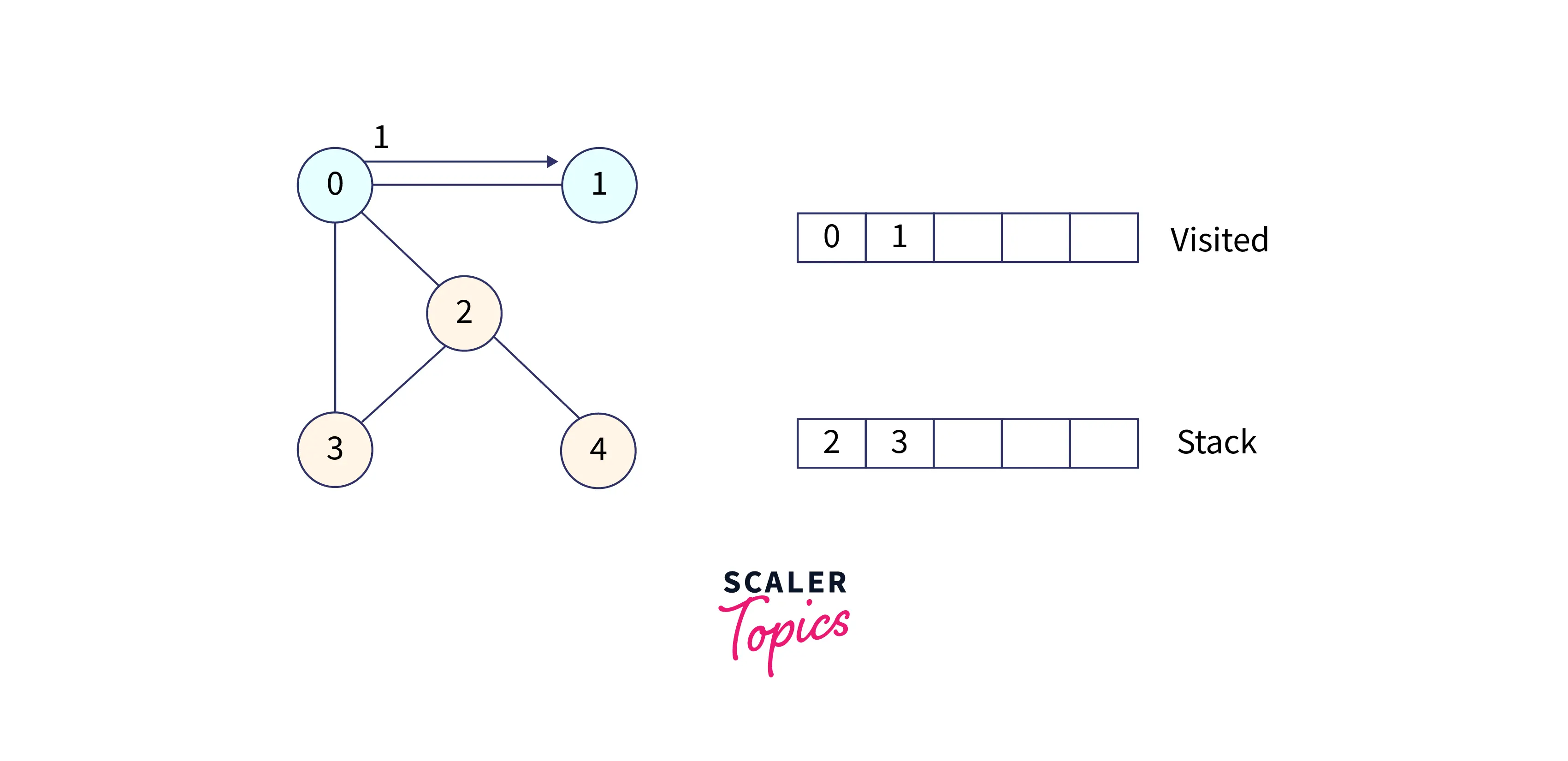
Now, we have 2 at the top of the stack, so visit it and put all of its adjacent nodes in the stack, since 2 has three adjacent nodes, which are 0, 3, and 4. But 0 is visited, and 3 is in the stack, so just put node 4 in the stack.
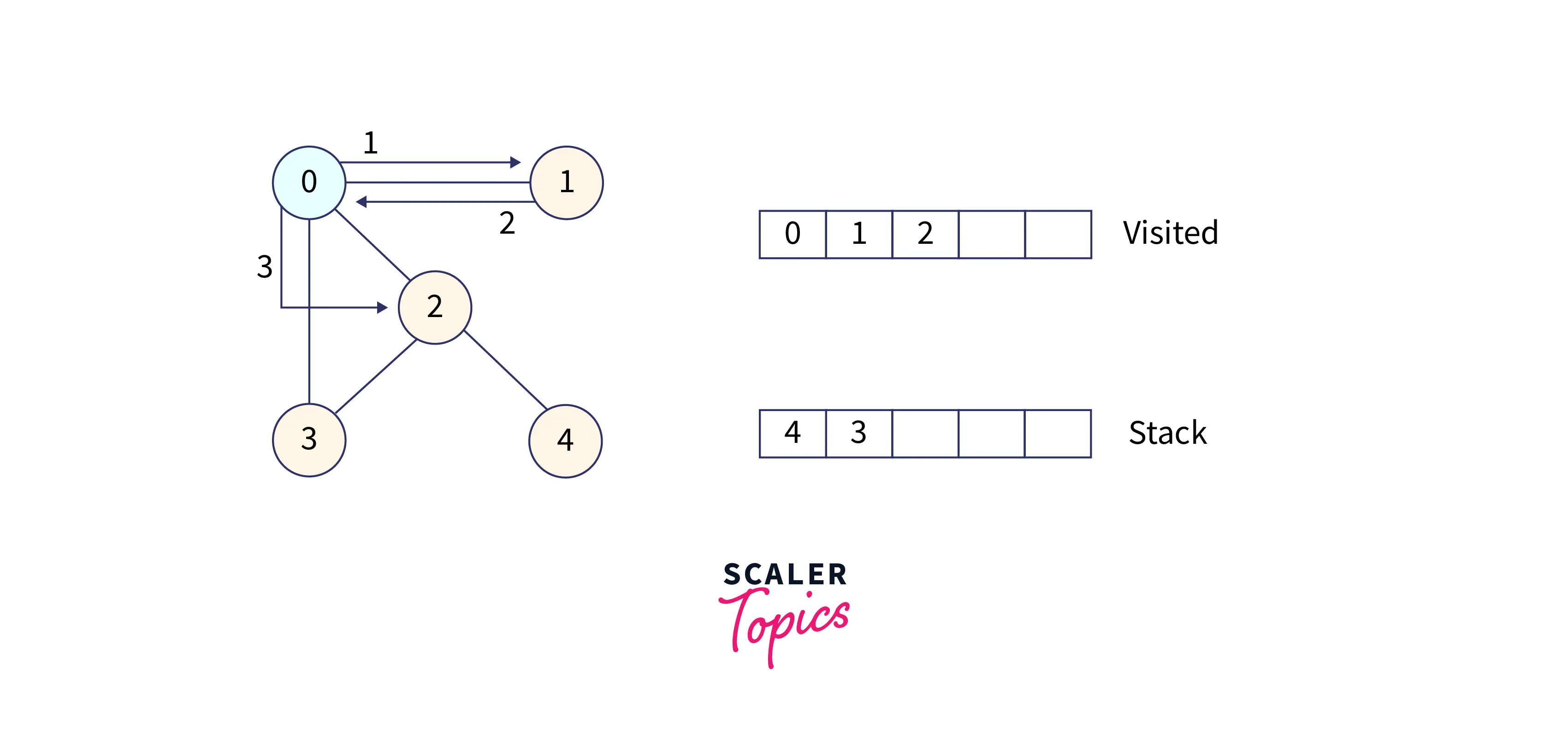
Now, we have 4 at the top of the stack, so pop 4 from the stack and visit it. Since 4 has only one adjacent node, i.e., 2 and it has already been visited, so move forward.
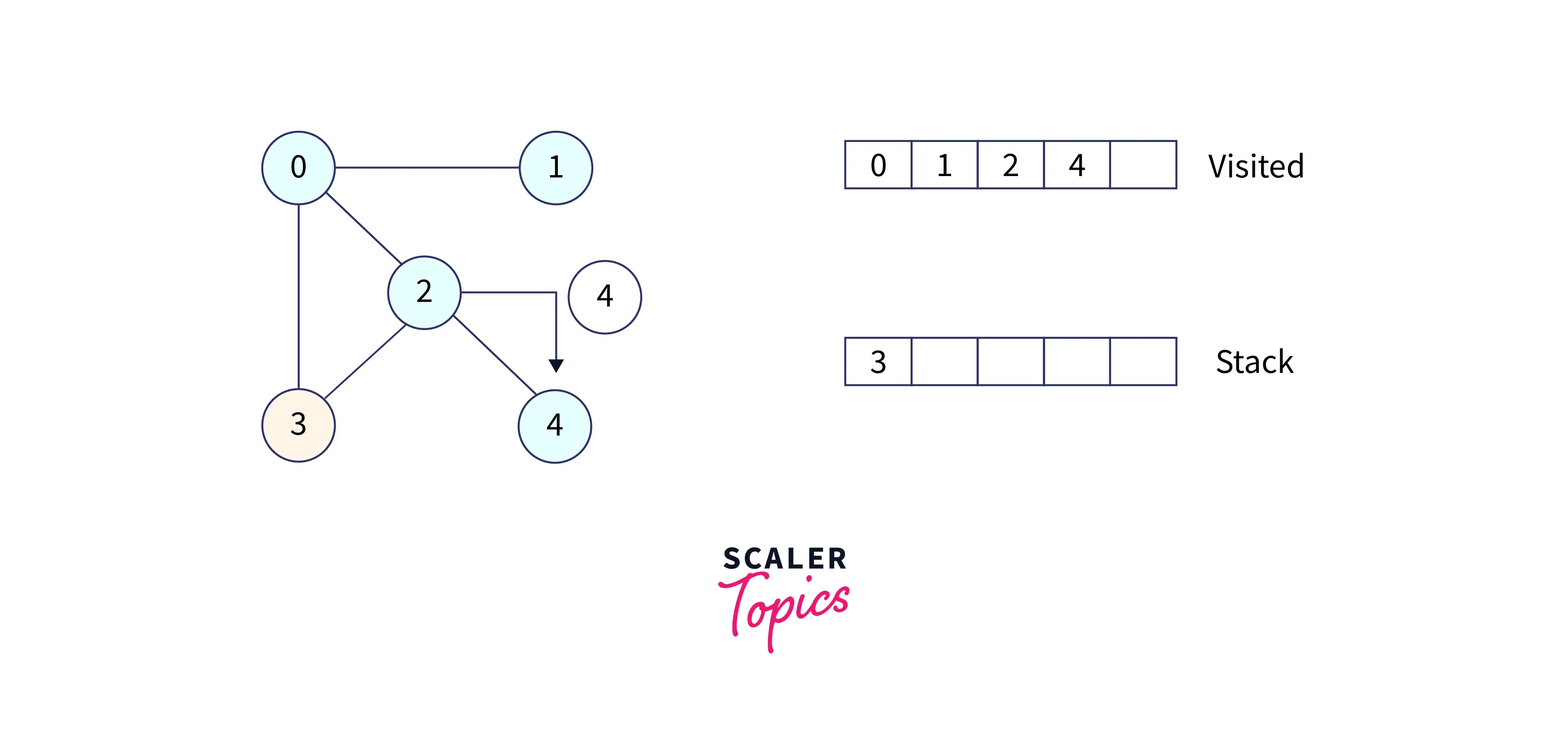
Now, we have only 3 left in the stack, so pop 3 from the stack and visit it. Our stack becomes empty, which means we have visited all the nodes and our DFS traversal ends.
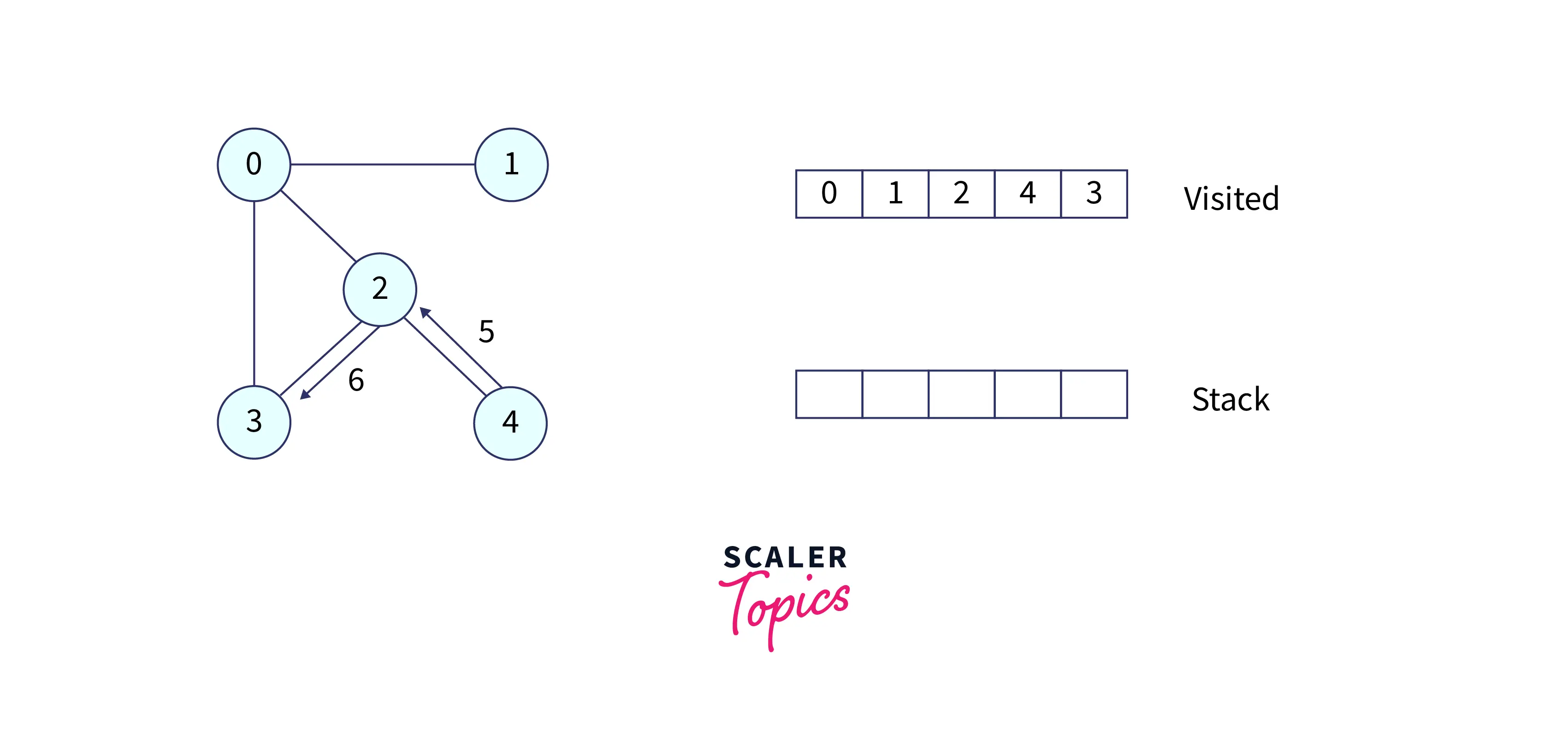
Example 2
We have taken an undirected graph with 5 vertices.
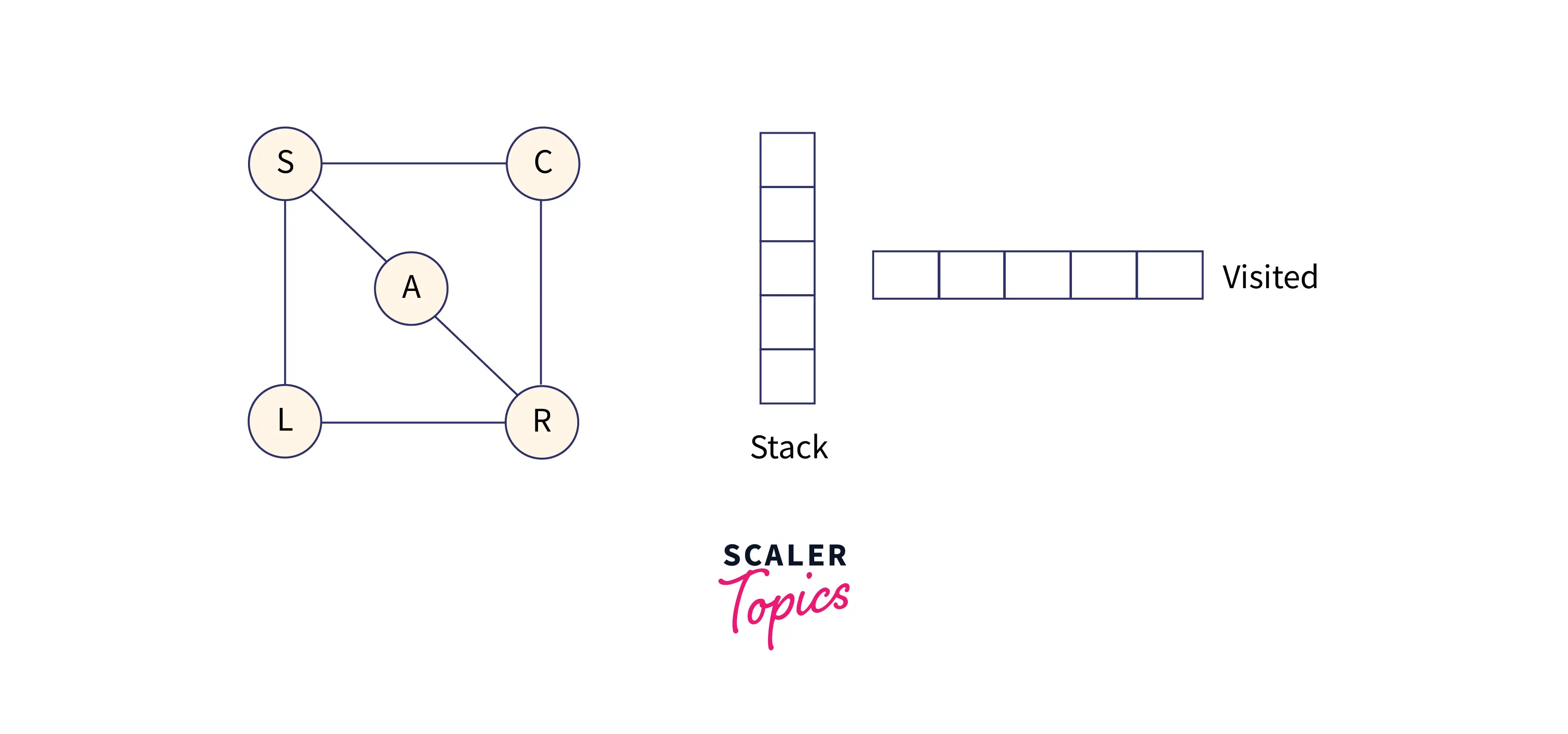
Below is the adjacency list of the above graph:
Start with node S, visit it, and put S into the stack. From node S, explore any unvisited node. We have three adjacent nodes from S, so we can choose anyone, but alphabetically we'll choose node A.
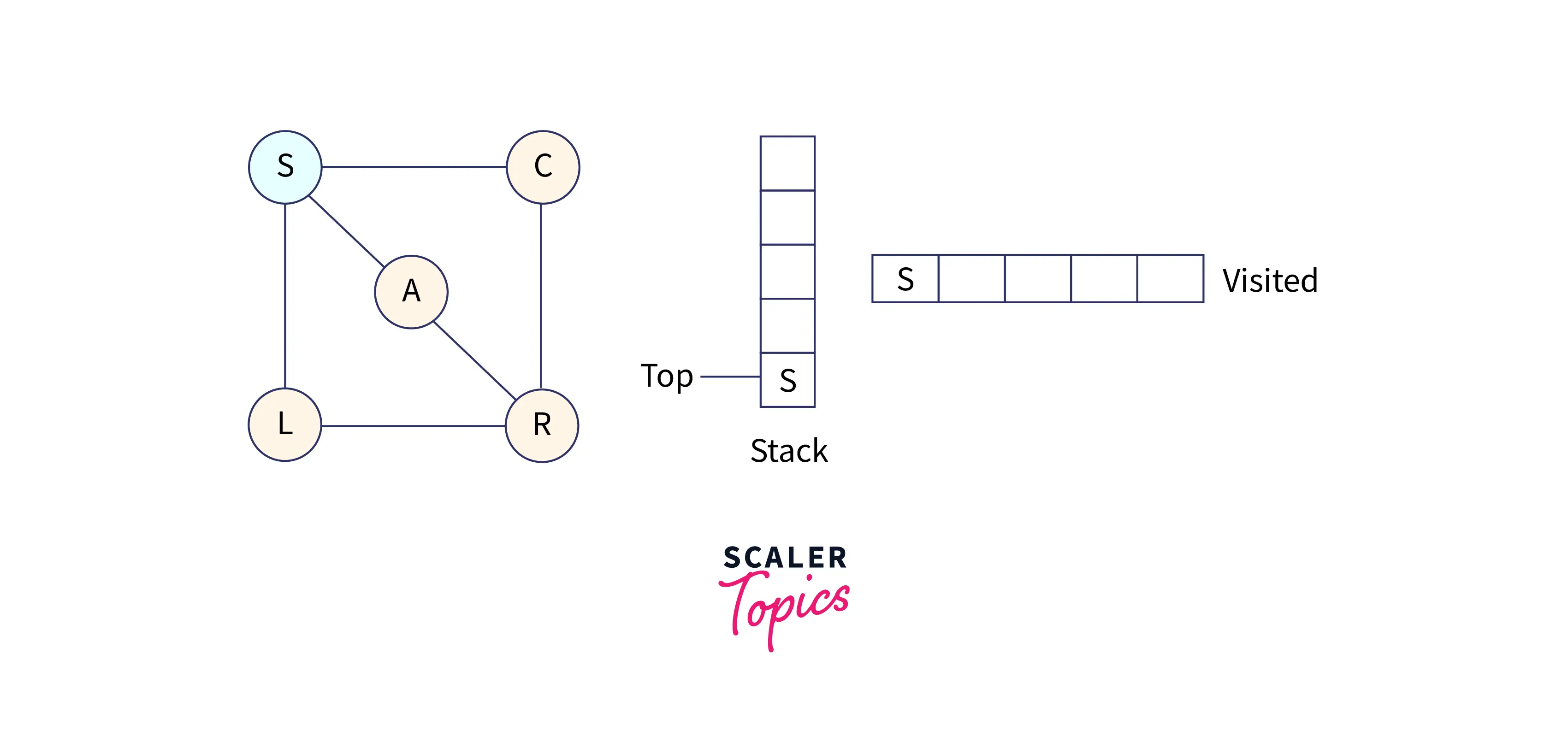
Mark A as visited and put it into the stack. Explore the unvisited nodes from A.
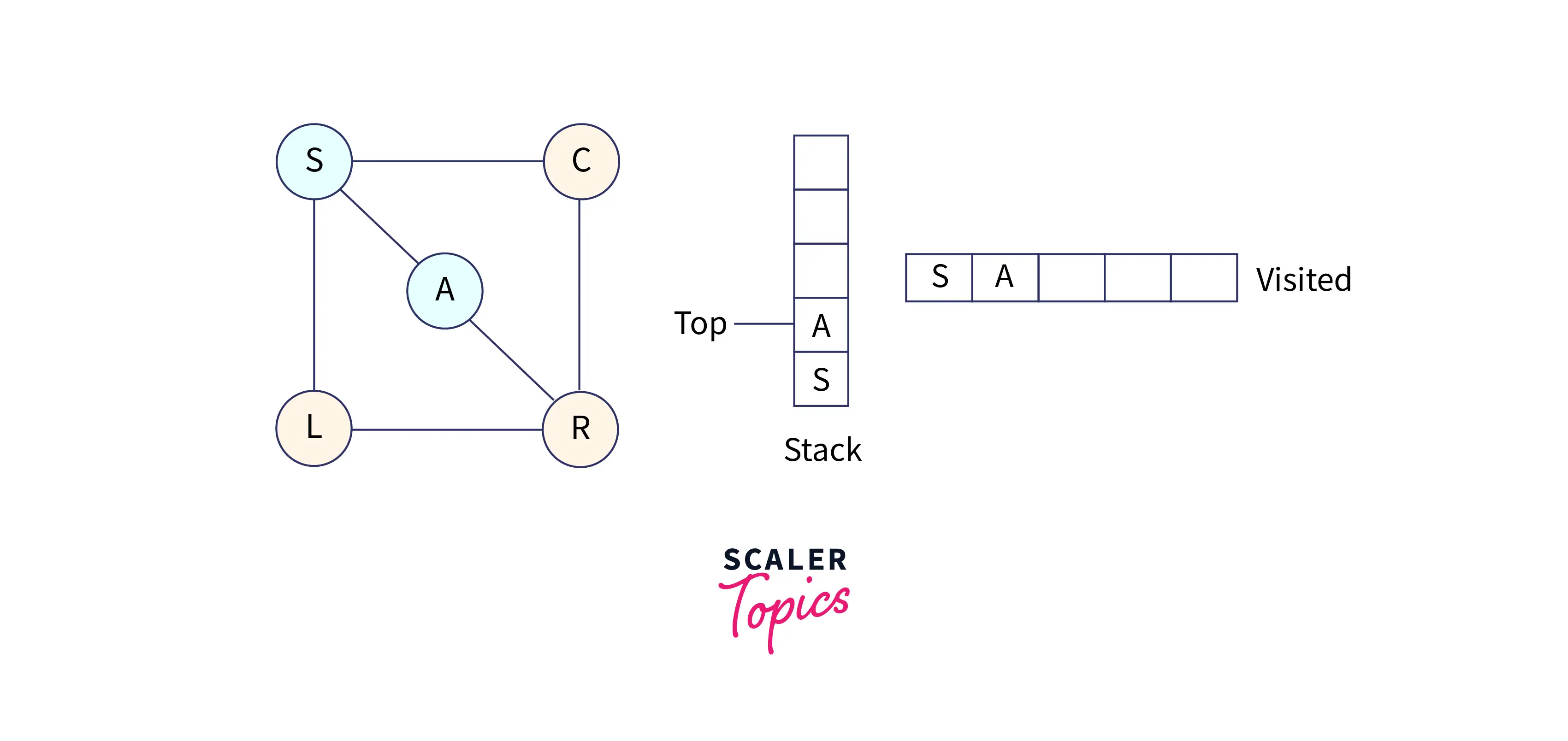
So, choose node R, mark it as visited, and put it into the stack. Now explore all the unvisited nodes from R. R has three adjacent nodes, i.e., A, L, and C, but C and L are unvisited.
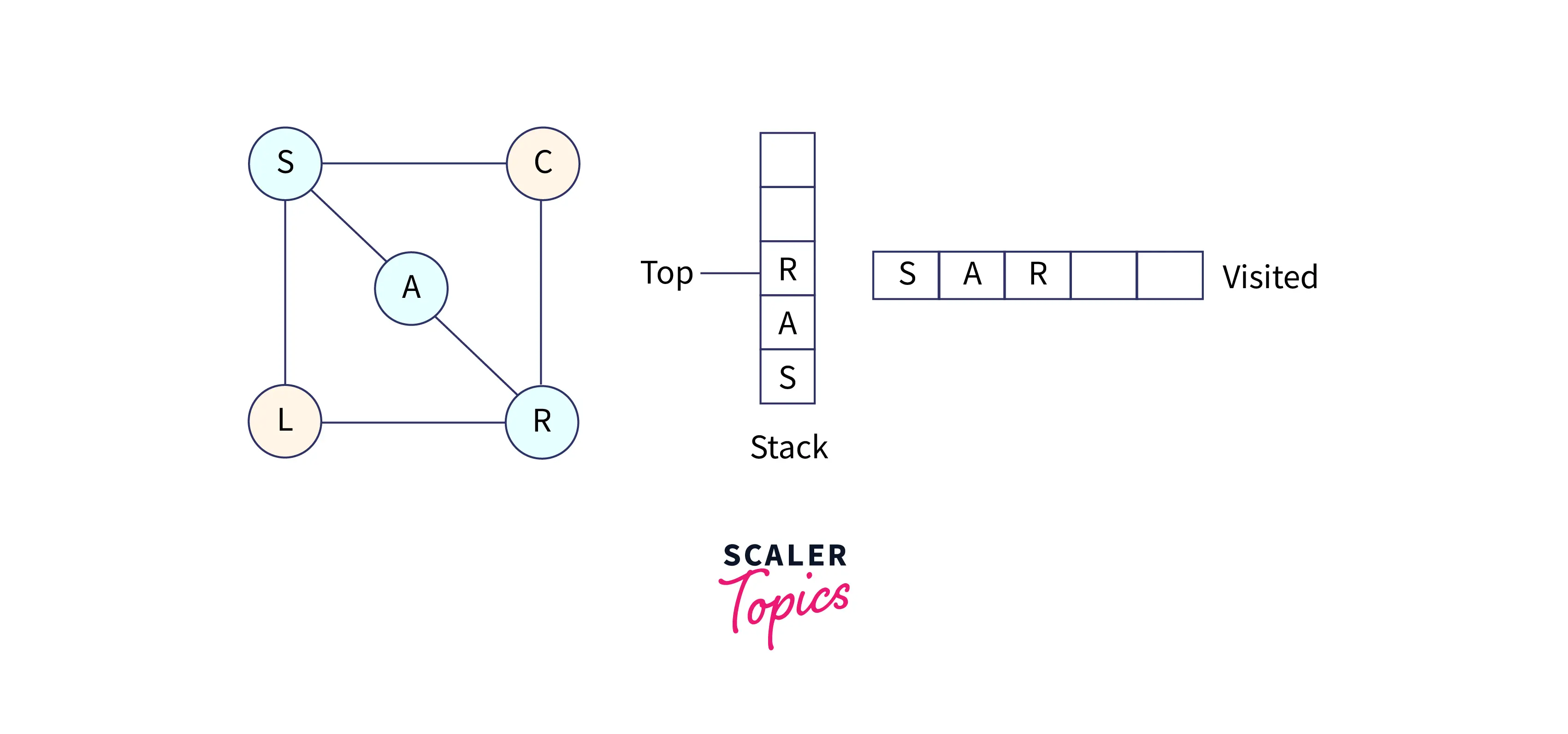
Now, choose node C, mark it as visited, and put it into the stack. Now C doesn't have any adjacent nodes that are unvisited.
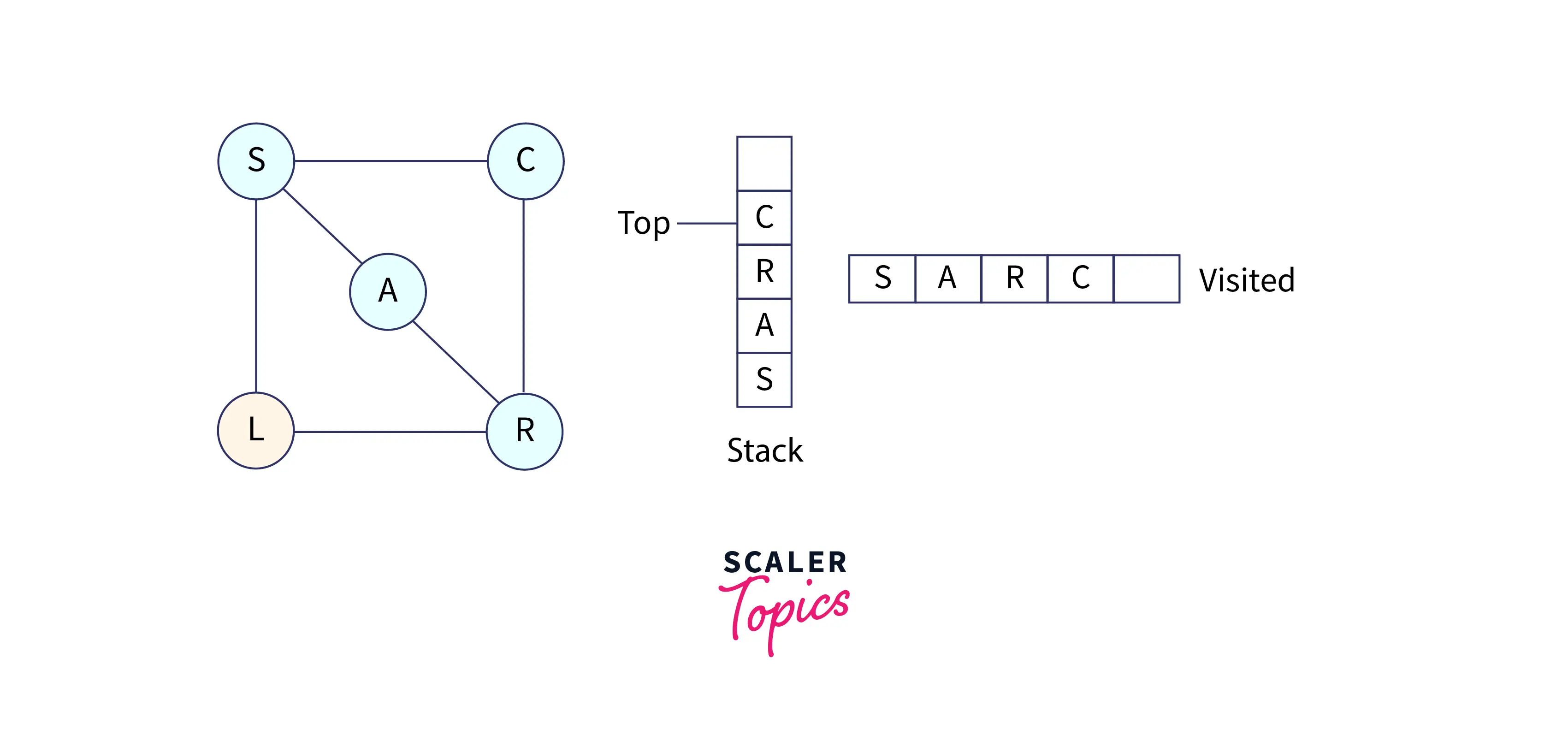
So, pop C from the stack; now we have node R at the top of the stack.
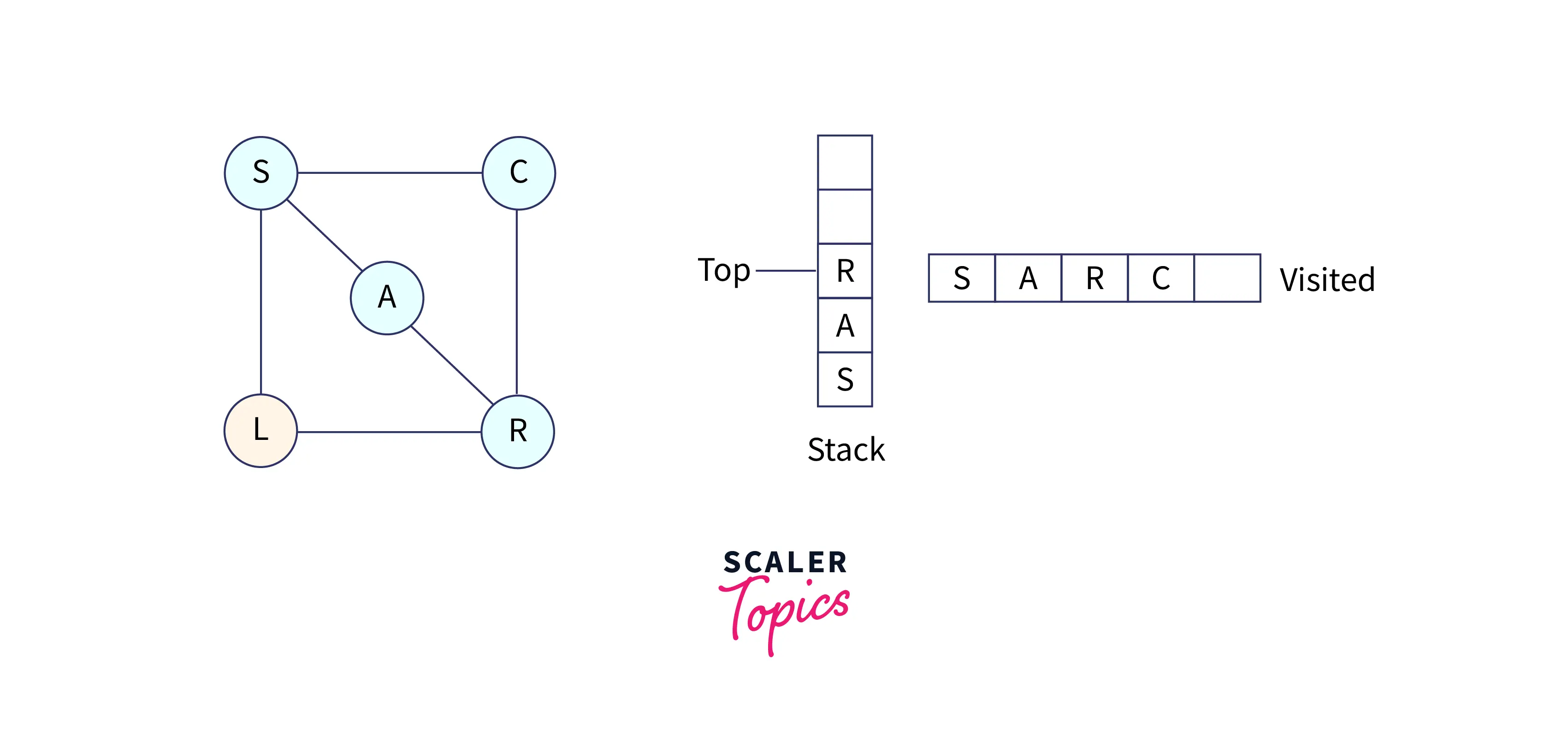
R has one node that is unvisited. The node is L, so mark it as visited and put it into the stack.
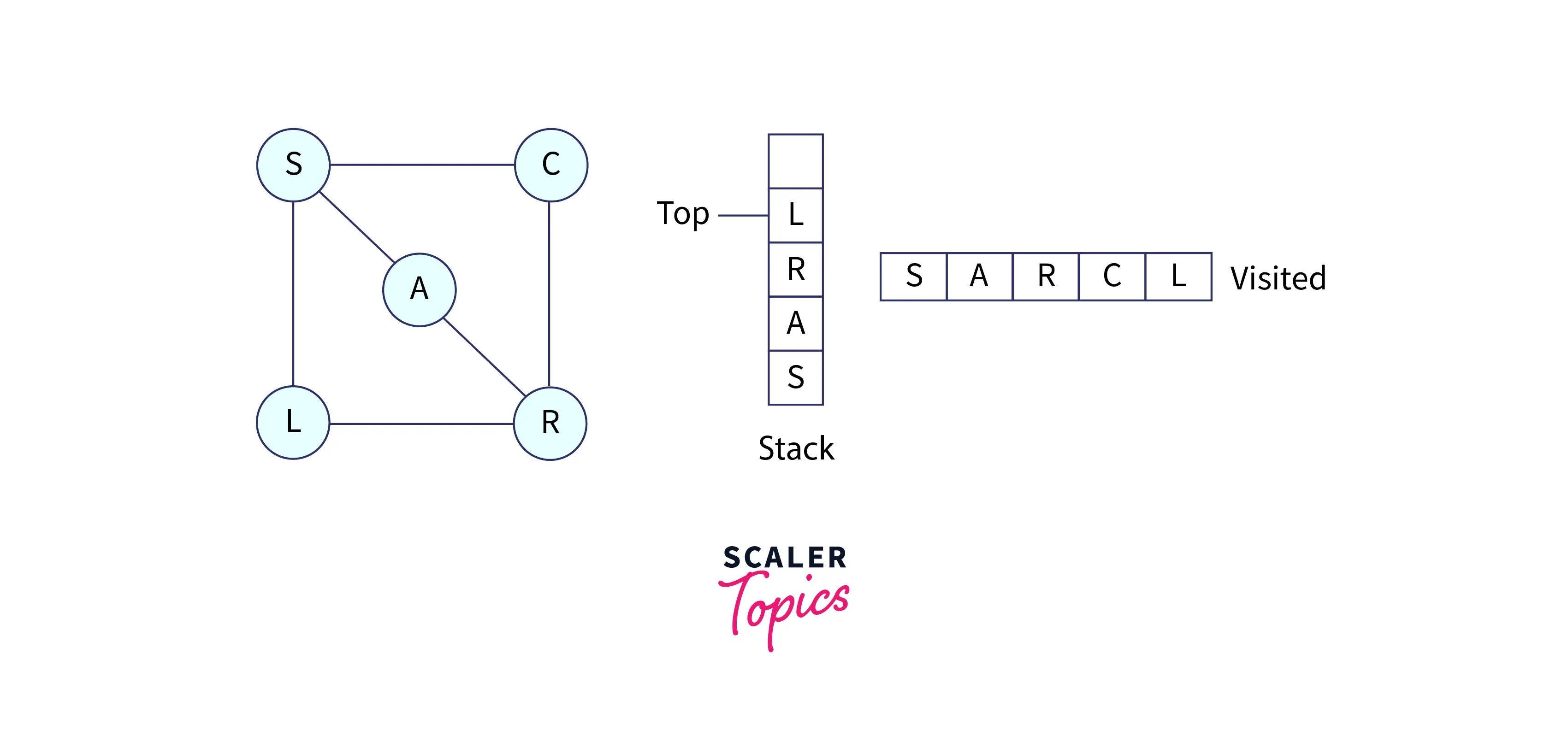
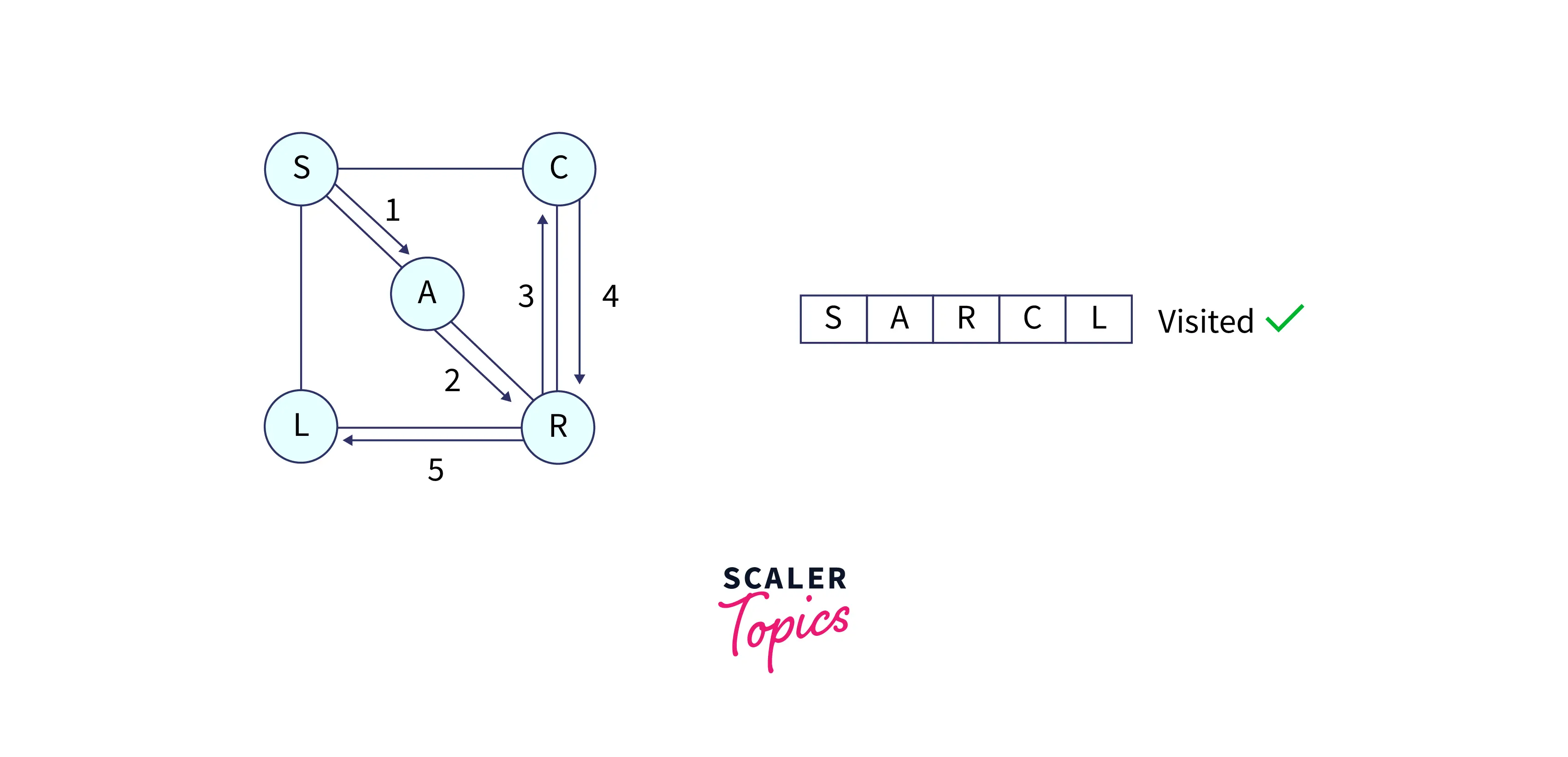
Since our visited array becomes full, that means all nodes have been visited. So we will end the traversal here and display the visited array.
In the below graph, you can see all the steps of our traversal.
Applications of DFS in Python
- Topological sorting, scheduling problems, cycle detection in graphs, and solving puzzles with just one solution, such as a maze or a sudoku puzzle, all use depth-first search.
- Other uses involve network analysis, such as detecting if a graph is bipartite.
- DFS is also used as a subroutine in graph theory matching algorithms such as the Hopcroft-Karp algorithm.
- Depth-first searches are used in route mapping, scheduling, and finding spanning trees.
Related Articles
You can prefer to read the below articles for more knowledge.
Conclusion
Let's conclude our topic on DFS Python by discussing some of the important points:
- DFS is diving deep into the graph and backtracking when it hits bottom. DFS is like solving a MAZE.
- In DFS, we continue to traverse downwards through linked nodes until we reach the end, then retrace our steps to check which connected nodes we haven’t visited and repeat the process.
- To implement DFS, we use the Stack data structure to keep track of the visited nodes.
- On a directed graph, the average time complexity of DFS is O(V+|E|), and for an undirected graph, it is O(V+2|E|)(each edge is visited twice). DFS on a tree has an average time complexity of O(V).
- Depth-first searches are used in route mapping, scheduling, and finding spanning trees.
