Graph Traversal in Data Structure
Learn via video course

Overview
A graph is a non-linear data structure, which is represented by vertices(nodes) and edges. Every pair of vertices is connected with one edge between them. Graph has many real-life applications, which we can see in our day-to-day life. For example, graphs are used widely in networking area, like social media networks, telephone networks, etc., where a single user can be represented as a node and the relationship between the users can be represented as edges.
Scope of the Article
Graph is one of the most used data structure in every field,so it is important to understand the working of graph In this tutorial, we will learn everything related to the Graph , its theory as well as algorithms. Below is an overview of what we will be studying.
- Introduction to Graph
- Cycle detection in graph
- BFS with multiple sources
- Topological sort
- Shortest path in a graph (Weighted and Unweighted)
- Spanning Tree and Minimum spanning tree
- Kosaraju's algorithm
:::
Takeaways
We have two famous algorithms to find the minimum spanning tree:
- Prim's Algorithm
- Kruskal's Algorithm
Graph Introduction
A graph is defined as an ordered set (V, E), where V represents the set of vertices, and E represents the set of edges that connect these vertices.
Example :
V(G) = {0,1,2,3,4} E(G) = {(0,1), (0,4), (1,2), (1,3), (1,4), (2,3), (3,4)}
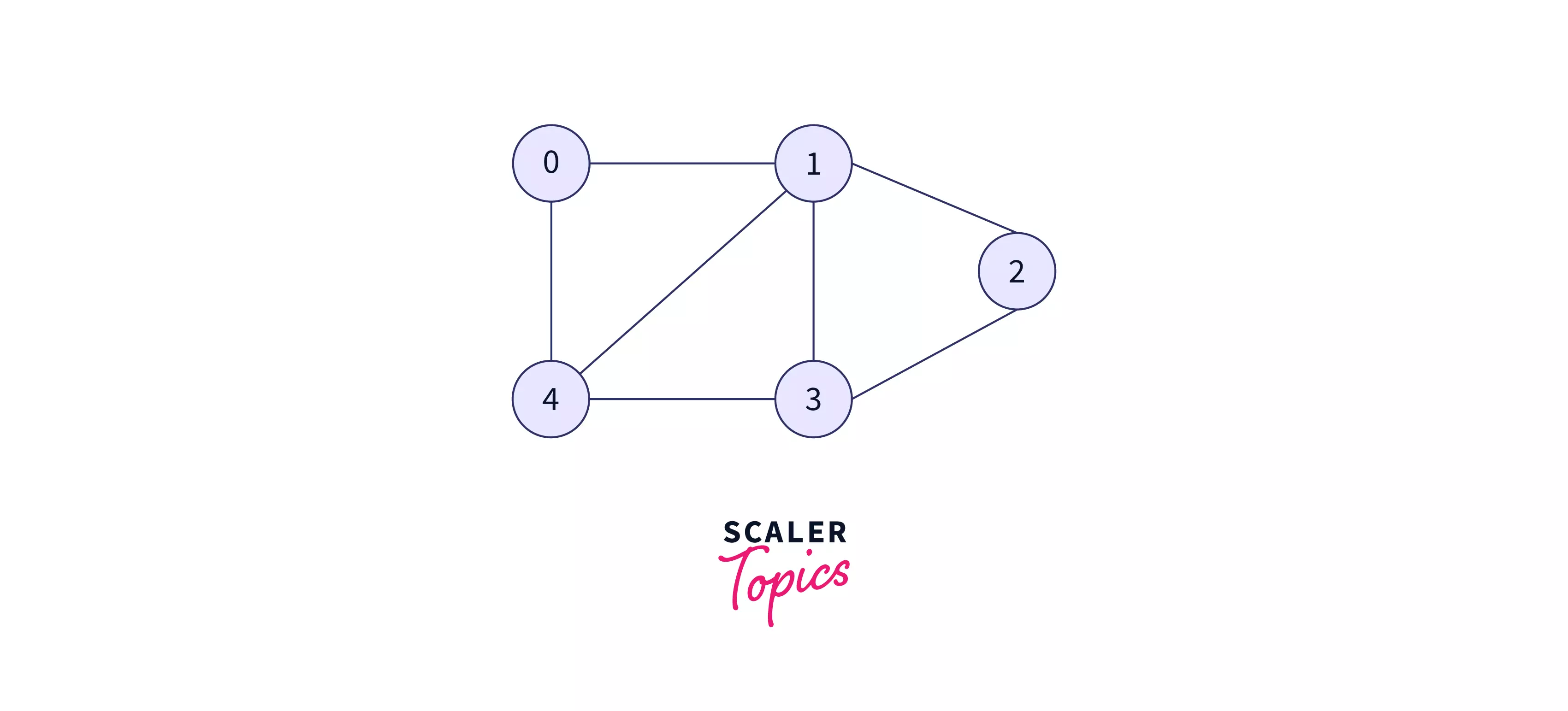
The above example shows the graphical representation of the vertices and edges.
Types of Graph
Graphs can be classified into two types:
Undirected Graph: A graph in which the edges do not have any directions associated with them, is known as an undirected graph.
Directed Graph: A graph in which the edges have a particular direction associated with them, is known as a directed graph.
Graphs Representation
A graph is mainly implemented in two following ways:
Adjacency matrix :
In this type of representation, we create a 2D array, and each cell (i,j) represents if there is an edge that exists between node i and node j. If the value at cell (i,j) is 1, then there is an edge between i and j, else if the value is 0, then there is no edge.
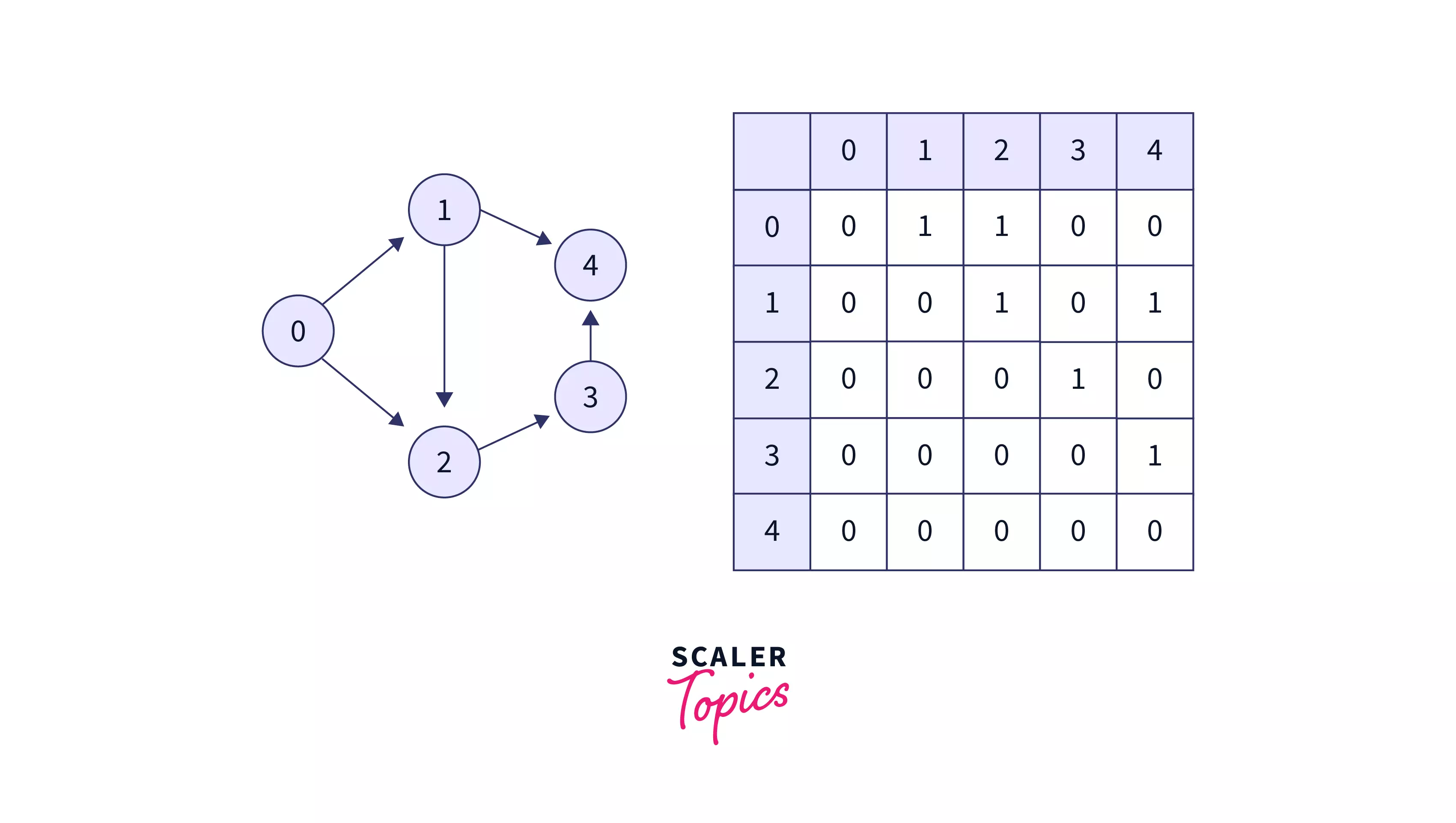
Note: The above representation is for a directed graph, in an undirected graph both the cells (i,j) and (j, i) is represented as 1 because in an undirected graph we consider an edge from both sides.
Adjacency List :
In this type of representation, we create an array of vertices, but this time, each vertex will have its list of edges connecting this vertex to another vertex
Below is the representation of the adjacency list
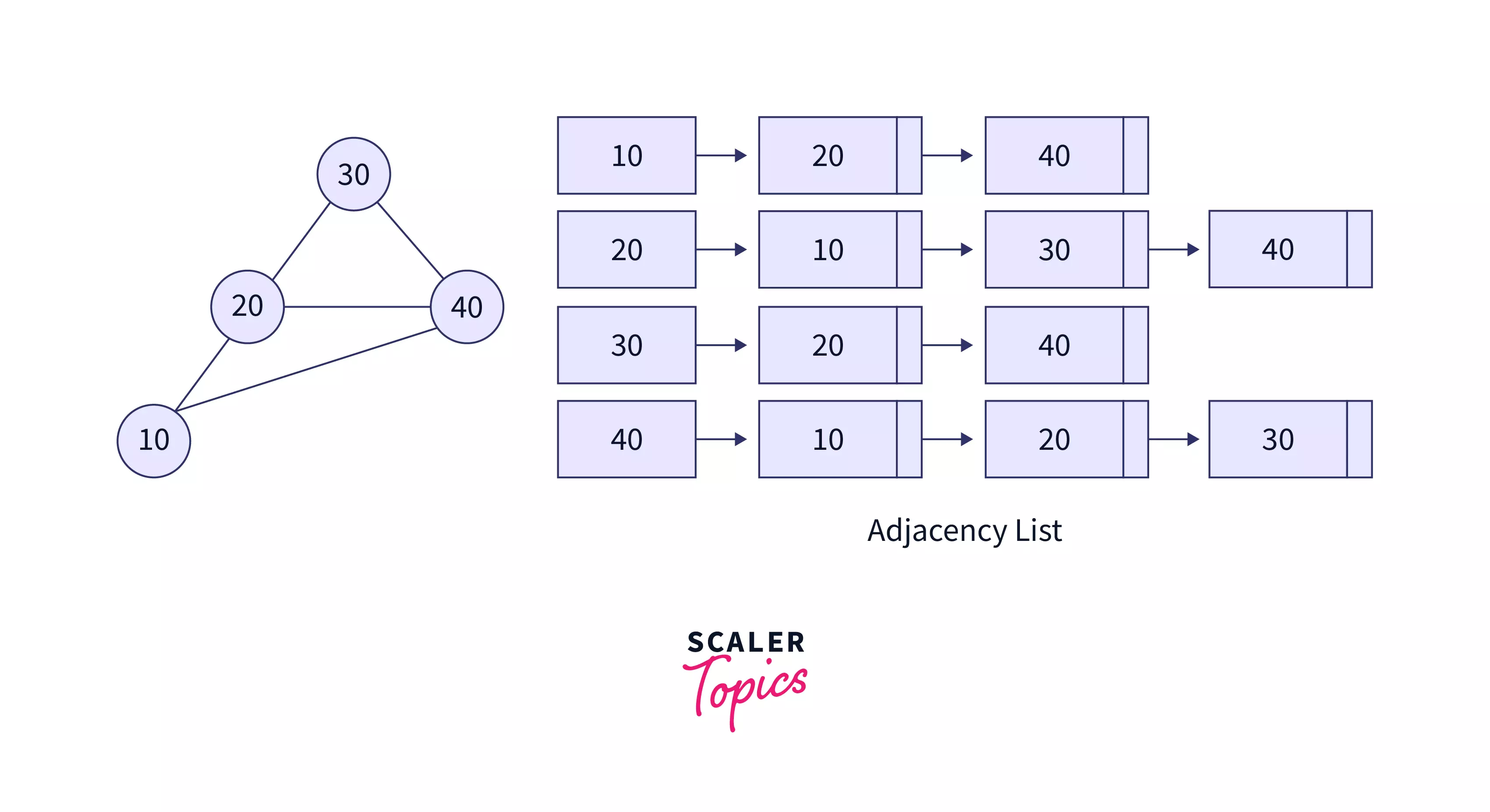
Graph Traversal
In simple words, traversal means the process of visiting every node in the graph. There are 2 standard methods of graph traversal Breadth-First Search and Depth First Search
Breadth First Search
Breadth-First Search (BFS) is a graph traversal algorithm, where we start from a selected(source) node and traverse the graph level by level, by exploring the neighbor nodes at each level.
For complete details about BFS, visit Breadth First Search
Depth First Search
Depth First Search (DFS) is a graph traversal algorithm, where we start from a selected(source) node and go into the depth of this node by recursively calling the DFS function until no children are encountered. When the dead-end is reached, this algorithm backtracks and starts visiting the other children of the current node.
For complete details about DFS, visit Depth First Search
Detect Cycle in Directed Graph
Given a directed graph, we have to check whether the graph contains a cycle or not.
Cycle Detection using BFS
Algorithm :
- Compute the in-degree of every node in the graph
- Make a visited array of nodes and initialize the count of each node as 0 initially
- First pick all the nodes with in-degree as 0 and push them into a queue
- Repeat the following steps until the queue becomes empty
- Start removing the nodes from the queue
- Decrease the in-degree of all the nodes attached by this node by 1, if the in-degree of any of these attached nodes is 0, then push them into the queue
- While pushing the node into the queue, increment the value of count by 1
- Finally, check if the number of visited nodes is equal to the number of nodes in the graph, the graph does not contain a cycle, else it contains a cycle
Note: Indegree of a node is the total number of edges that are coming to that node.
Implementation :
Cycle Detection using DFS
Algorithm :
- Make a visited array of size N (number of vertices)
- Make a recursive DFS function that takes the current node, and visited array as arguments
- Make a recursion visited array to track the nodes visited in the current recursion
- Make the current node as visited and call the recursive DFS function with the adjacent node ad current node
- If at any point the adjacent vertex is already visited, then return true
- Else if all the nodes are visited, return false
Implementation
:::
Detect Cycle in Undirected Graph
Given an undirected graph, we have to check whether the graph contains a cycle or not.
Cycle Detection using BFS
Algorithm :
- Create an empty queue of pair and push the starting node in it with a -1 value.
- In the pair, the first value denotes the node value and the second value denotes the parent of this node.
- Create a visited array to keep the track of visited nodes
- While the queue is not empty, do the following
- pop the front element from the queue
- start traversing this node in the adjacency list
- if this node is not visited, mark it as visited and push the node into the queue with the first value as node number and the second value as the parent
- else if the node is visited, check the parent value, if the parent value is not the same, then return true
- else continue
Implementation
Cycle Detection using DFS
Algorithm :
- Make a visited array of size N (number of vertices)
- Make a recursive DFS function that takes the current node, parent node, graph, and visited array as arguments
- Make the current node as visited and call the recursive DFS function with the adjacent nodes of this current node
- If the recursive function returns true, then return true from here also
- Else If at any point the adjacent vertex is already visited, and the parent node is not the same as the current node, then return true
- Else if the loop ends without returning true, return false
Implementation
BFS with Multiple Sources
BFS with multiple sources also known as multi-source BFS is also a graph traversal algorithm that works just like simple BFS. In simple BFS we start only from the given source node but in multi-source BFS we start from all the sources find the desired output in a minimum time.
We can understand the multi-source BFS with the following example
Problems
Given a binary matrix and the destination cell, we can start from any cell which has a value equal to 1. In 1 second we can go from one cell to another cell that is adjacent to it. Find the minimum number of seconds to reach the destination cell.
Input : [0,0,1,0] [1,0,0,1] [0,0,0,0] [0,1,0,0]
Destination cell : (2,3)
Output : 1
Explanation:
We can reach the cell (2,3) by starting from the cell (1,3) because it is considered one of the source nodes. By starting from any other node, we can't reach (2,3) in 1 second.
Algorithm
- Create an empty queue of pair and push all the cells whose value is 1
- Create a visited 2D array to keep track of visited cells
- Create a variable named answer and initialize it with 0, as we visit each level in the queue, we increment the count of answer.
- While the queue is not empty, do the following
- take the node out from the queue, and check if it is already visited or not
- if it is already visited then continue
- else mark it as visited and push all the adjacent cells of this cell to the queue
- if at any point we reached the destination cell, then break out from the while loop
- return the answer
Implementation
Topological Sort
A topological sort in a directed acyclic graph is the linear ordering of its vertices, such that for its every edge u->v, u comes before v in the ordering.
For complete details about topological sort visit Topological sort
Shortest Path in an Unweighted Graph
Given an unweighted graph and a source node. We have to find the shortest distance for every node from the given source node.
Algorithm
- Create an empty queue and put the source node into the queue
- Create a distance array, initialize every element of this array to be the largest number (INT_MAX in C++), and initialize the source node distance as 0
- While the queue is not empty, do the following
- pick the top most element from the queue and remove it from the queue
- check its distance from the source node, let it be d
- check all the neighbors of this node and check their distance from the distance array
- for every neighbor, if the distance is more than d+1, then update the distance as d+1 and push it into the queue
- else continue
Implementation
Shortest Path in a Weighted Graph
Dijkstra's Algorithm
Given an unweighted graph and a source node. We have to find the shortest distance for every node from the source node.
Algorithm
- Create an empty min heap (priority_queue) of pair and put the distance of the node from the source node as the first element of the pair and node as the second element of the pair into the queue
- Create a distance array, initialize every element of this array to be the largest number (INT_MAX in C++), and initialize the source node distance as 0
- While the queue is not empty, do the following
- pick the top most element from the queue and remove it from the queue
- check its distance from the source node
- check all the neighbors of this node and check their distance from the distance array
- for every neighbor, if its the distance is more than next_dist+dist[node], then update the distance as next_dist+dist[node] and push it into the queue
- else continue
Implementation
Spanning Tree
A spanning tree is a part of an undirected connected graph (sub-graph), and it includes all the vertices of the graph with the minimum possible number of edges. A spanning tree can not be disconnected.
For complete details of Spanning Tree visit Spanning Tree
Minimum Spanning Tree
A minimum spanning tree is a spanning tree, which has the minimum total sum of all the weight of its edges.
We have two famous algorithms to find the minimum spanning tree:
Prim's Algorithm.
Prim's algorithm is a greedy algorithm that is used to find the minimum spanning tree. It starts building a minimum spanning tree from any selected vertex in the graph.
For details visit Prim's Algorithm
Kruskal's Algorithm.
Kruskal's algorithm is also a greedy algorithm that is used to find the minimum spanning tree. But unlike Prim's algorithm, it starts building a minimum spanning tree from the vertex carrying minimum weight in the graph.
For details visit Kruskal's Algorithm
Kosaraju's Algorithm
Kosaraju's algorithm is a DFS-based algorithm that is used to find the Strongly Connected Components (SCC) in the graph.
Strongly Connected Components
A strongly disconnected component is a portion of a directed graph in which every vertex is reachable from every other vertex.
Algorithm
- Create an empty stack
- Perform DFS on the graph and push the nodes in the stack
- Reverse all the edges of the graph
- While the stack is not empty, if the node is not visited, then perform the DFS on this node and print all the nodes coming in the order.
Conclusion
Graphs are one of the most important data structures and have many real-life applications. So it is important to understand the working of graph data structure. In this tutorial, we have learned everything related to the Graph Data Structure, its theory as well as algorithms.
